дроби »
примеры с дробями - страница 54
4m+7 - 5 : 3m-1
- = ?
3m-1 - 2m-1 :4m^2-1
Пример нужно решать по действиям первое деление, второе вычитание, задание 8 класса
Решение: Преобразование числителя
$$ 1)4m+7- \frac{5}{3m-1}= \frac{(4m+7)(3m-1)}{(3m-1)}- \frac{5}{3m-1}= \frac{12m^{2}+21m-4m-7-5 }{3m-1}= \\ =\frac{12m^{2}+17m-12 }{3m-1} $$
Преобразование знаменателя
$$ 2)3m-1- \frac{2m-1}{4m ^{2}-1 }=3m-1- \frac{2m-1}{(2m -1)(2m+1) }= 3m-1- \frac{1}{2m+1}= \\ = \frac{(3m-1)(2m+1)}{2m+1} - \frac{1}{2m+1}=\frac{6m^{2}-2m+3m-1-1}{2m+1} =\frac{6m^{2}+m-2}{2m+1} $$
Делим числитель на знаменатель
$$ 3)\frac{12m^{2}+17m-12 }{3m-1}:\frac{6m^{2}+m-2}{2m+1}=\frac{12m^{2}+17m-12 }{3m-1}\cdot\frac{2m+1}{6m^{2}+m-2}= \\ =\frac{12m^{2}+17m-12 }{3m-1}\cdot\frac{2m+1}{(3m+2)(2m-1)} $$(a^2-81b^2/a^2 : а b-9b^2/a- ) при а=50 b=20. Найти Значение и выражение.( ^ в квадрате) / (дробь черта) это просто скобки a^2-81b^2/a^2 : а b-9b^2/a- при а=50, b=20
Решение: $$ a^2-\frac{81b^2}{a^2} : ab-\frac{9b^2}{a} \\ \\ a^2-\frac{81b^2}{a^2}=\frac{a^4-81b^2}{a^2} \\ \\ ab-\frac{9b^2}{a}=\frac{a^{2}b-9b^2}{a} \\ \\ \frac{a^4-81b^2}{a^2}:\frac{a^{2}b-9b^2}{a}=\frac{a^4-81b^2}{a^2}*\frac{a}{a^{2}b-9b^2}=\frac{a^4-81b^2}{a}*\frac{1}{b(a^{2}-9b)}=\frac{a^4-81b^2}{ab(a^{2}-9b)}= \\ \\ =\frac{(a^{2}-9b)(a^{2}+9b)}{ab(a^{2}-9b)}=\frac{(a^{2}+9b)}{ab} $$
при а=50, b=20
$$ \frac{(a^{2}+9b)}{ab}=\frac{(50^{2}+9*20)}{50*20}=\frac{(2500+180)}{1000}=\frac{2680}{1000}=2,68 $$\(\frac{(4m-1)!}{(4m-3)!} \)
Решение: По определению n!=1*2*3*.*(n-2)*(n-1)*n(4m-1)!=1*2*3*.*(4m-3)*(4m-2)*(4m-1)=(4m-3)! *(4m-2)(4m-1)
Заменили произведение первых множителей до (4m-3)-го включительно обозначением через факториал.
(4m-1)! (4m-3)! (4m-2)(4m-1)
- = - = (4m-2)(4m-1)
(4m-3)! (4m-3)!
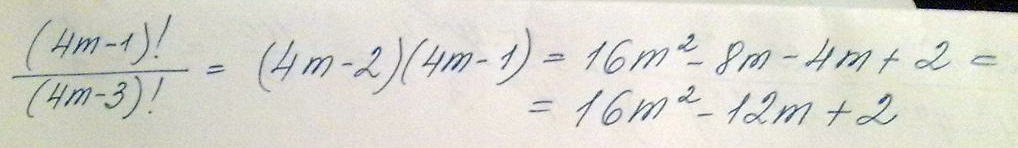
Решите графическое уравнение 4/х=-х
Решение: Вообще нужно построить на одной координатной плоскости 2 графика: для y=4/x и для y=-x и посмотреть их точки пересечения. Но в данном случае рациональных корней скорее всего существовать не будет, так как графики не имеют на поле действительных чисел общих точек. мнимые корни считаются вручную: 4/x=-x, 4=-x^2, x^2=-4, x1=-2i, x2=2iРешить:
1)(√3-2√2)(√3+2√2) дробь деления 7/8 -0,125 + 1/20
2) 0,625+1/8+2(в нулевой степени) -2 (в степени -1) дробь деления (√2-1)(√2+1)
3) (2+2√2+1)(√2-1)<- (эта скобка во второй степени). дробь деления (0,05в нулевой степени)+ 0,75-1/4,
третье уравнение полностью в скобках в степени -1
Решение: 1)(√3-2√2)(√3+2√2) /( 7/8 -0,125 + 1/20)=1,25
(√3-2√2)(√3+2√2)=9-8=1
7/8 -0,125 + 1/20=7/8-1/8 +1/20=3/4+1/20=15/20+1/20=16/20=4/5
1:4/5=5/4=1,25
2) (0,625+1/8+2^0 -2^ ( -1)) / (√2-1)(√2+1)=1,25
0,625+1/8+2^0 -2^ ( -1)=0,625+0,125+1-0,5=1,25
(√2-1)(√2+1)==2-1=1
1,25:1=1,25
3)[(2+2√2+1)(√2-1)²/ (0,05^0 + 0,75-1/4)]^-1=1,5
(√2 +1)²(√2 -1)²=(2-1)²=1
0,05^0 + 0,75-1/4=1+0,75-0,25=1,5
1:1,5=2/3
(2/3)^-1=3/2=1,5

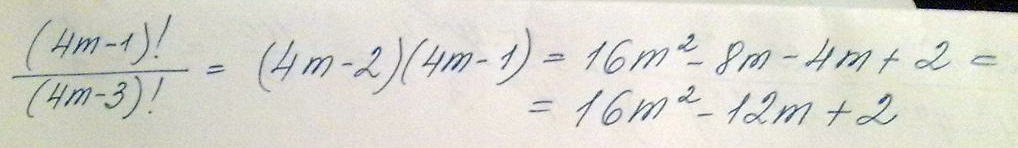
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...