производная »

график функции производной - страница 3

  • На рисунке изображен график производной функции f(x), определенной на интервале (-4;4). Найдите абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой y=3x+5 или совпадает с ней.


    Решение: На рисунке изображен график производной функции f(x), определенной на интервале (-4;4). Найдите абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой y=3x+5 или совпадает с ней.
    Решение:
    У параллельных и совпадающих прямых их угловые коэффициенты равны или
      k1= k2.
    В нашем задании угловой коэффициент параллельной прямой задан.
     Он равен
       k2 = 3.
     Поэтому угловой коэффициент касательной равен
       k1= k2 = 3.
      Угловой коэффициент касательной к функции в точке хо равен производной функции в этой точке y’(xo).
       k = y’(xo) =3
    В задании задан график производной этой функции на интервале (-4;4).
    Найдем на этом интервале точку с значением производной равной 3 или ординатой (значением у) равной 3.
        Координаты этой точки
       (-1;3).
     Поэтому в точке с абсциссой х = -1 уравнение касательной к графику функции будет параллельно прямой y=3x+5 или совпадает с ней.
     Ответ: -1

  • На рисунке изображен график производной функции y=f(x), определенной на интервале (-8;3). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=8


    Решение: У прямой у=8 угловой коэффициент k=0
    Значит и у касательной, он должен быть равен 0.
    k(касательной)=f`(x₀)
    f`(x₀)=0
    Это те точки, в которых график у=f`(x) на рисунке пересекает ось ох
    х₀=-7  и  х₀=-5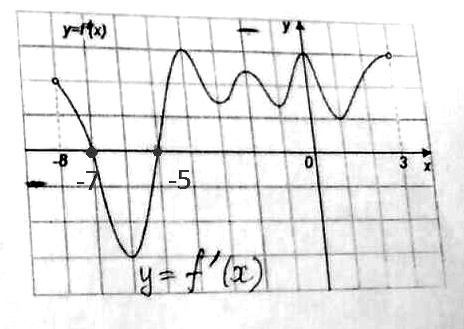

    У прямой у угловой коэффициент k Значит и у касательной он должен быть равен .k касательной f x f x Это те точки в которых график у f x на рисунке пересекает ось охх -   и  х...

  • На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна y =x+1 или совпадает с ней.


    Решение: Известно, что значение производной в точке есть угловой коэффициент касательной к графику функции в этой точке, то есть  $$ k=f’(x_0). $$  
    Прямая  у=х+1 имеет угловой коэффициент  к=1 (коэффициент
     перед х). А параллельные прямые имеют равные угловые коэффициенты. Значит, на графике мы должны найти точки, в которых
     $$ f’(x_0)=1. $$ 
    Таких точек три, потому что  график  y=f’(x) пересекается
    с прямой у=1  в трёх точках.

  • На рисунке изображен график производной функции y = f(x), определенной на интервале (–5; 9).
    Найдите количество точек, в которых касательная к графику функции y = f(x) параллельна прямой y= - 2x-31 или совпадает с ней.


    Решение: Таких точек 5.
    Так как касательная параллельна прямой у=-2х-31, то
    угловой коэффициент касательной будет совпадать с
    угловым коэффициентом прямой  у=-2х-31, который равен
    коэффициенту перед переменной х, то есть  к=-2.
     Но  $$ k=f’(x_0)=-2 $$.  Поэтому надо найти количество  точек
    пересечения графика f ’(x) с прямой у=-2. Таких точек 5.

  • На рисунке изображен график производной функции F(x), определенной на интервале (-6;6). В какой точке отрезка [-3;3] f(x) принимает наименьшее значение


    Решение: График производной пересекает ось х в двух точках: х = -5 и х = 2
     Слева от х = -5 производная >0, справа <0, значит точка х = -5 - это точка максимума.
    Слева от х = 2 производная <0, справа >0, значит, точка х = 2 - это точка минимума.
    Ответ: В точке х = 2 функция f(x) принимает наименьшее значение 

<< < 123 4 5 > >>