производная »

график функции производной - страница 5

  • на рисунке изображён график функции f ’ (x) - производной функции f(x) определенной на интервале (-3,8). Найдите точки минимума функции f(x)


    Решение: Если график производной лежит выше оси Ox, то сама функция возрастает.
    Если график производной лежит выше оси Ox, то сама функция убывает.
    Точка минимума - точка в которой убывание функции сменяется возрастанием.
    Смотрим на производную. Видно что подходит точка 4.

  • На рисунке изображен график y=f ’ (x) — производной функции f (x), определенной на интервале(-13;5). Найдите количество точек максимума функции f (x), принадлежащих отрезку[-11;4].


    Решение: Критические точки - это точки в которых производная равна нулю, т е график производной пересекает ось Ох. Таких точек три: х=-10, х=-2, х=3.
    В точке максимума производная меняет знак с "+" на "-", такая точка одна: х=-2 (слева от этой точки значения производной выше оси Ох, справа - ниже)

  • На рисунке изображен график функции у=f(x) - производной функции f(x), определенной на интервале (-3;8) найдите точку минимума


    Решение: касательная параллельна прямой y=-20 означает, что производная равна нулю (так как производная от -20 по x будет 0)
    вот и находите точки на интервале (-8,3) где производная равна нулю.
    их две: -7 и 2
    ps: для Alasska.
    "а значит нужно посчитать колличество знакаперемен у проиводной "
    глупостей не говорите только. функция не обязана менять свое поведение. она может возрастать, потом идти параллельно оси ОХ и снова возрастать (открывайте учебник, читайте про точку перегиба) ! Производная при этом знак не поменяет (ну если только не считать 0 сменой знака), а вот через 0 пройдет. Поэтому все определяется не точками экстремума.
    плюс интервал от -8 до 3, а не от -9, до 9. а нулей производной на интервале от -8 до 3 всего 2!
    для общей информации - касательная к кривой в точке паралельна прямой y=k*x+b, если производная функции описывающей кривую в этой точке равна k (производная определяет "наклон" касательной). для y=-20 k=0, поэтому и производная должна быть равна нулю. и речь ни о каких экстремумах вообще идти не должна.
    и прежде чем ставить "2" за ответ - убедитесь в правильности своего.

  • На рисунке изображен график функции y=f(x) - производной функции f(x), определенной на интервале (-3;8). Найдите точку минимума функции f(x).


    Решение: Необходимое условие экстремума: производная равна нулю.
    Производная данной функции обращается в ноль в точках -2 и 4
    Эти точки являются точками возможных экстремумов. Чтобы узнать есть в каждой из этих точек экстремум надо воспользоваться теоремой- достаточное условие экстремума функции.
    х₀- точка, в которой производная равна нулю. Если при переходе через точку х₀ производная меняет знак с "+" на "-", то х₀- точка максимума, если с "-"  на "+", то точка минимума.
    При переходе через точку х=4 производная меняет знак с "-" на "+"
    График расположен ниже оси ох, а после точки 4 выше оси ох.
    х=4 - точка минимума

    .

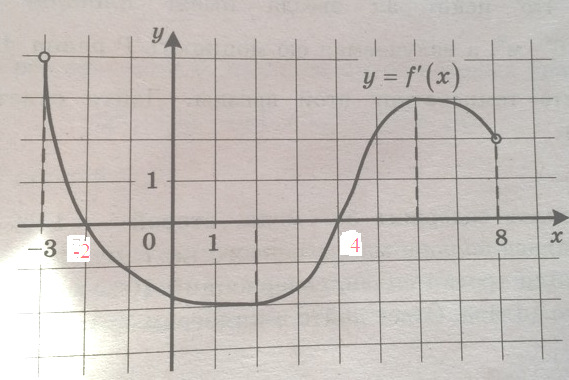
    Необходимое условие экстремума производная равна нулю.Производная данной функции обращается в ноль в точках - и Эти точки являются точками возможных экстремумов. Чтобы узнать...

  • на рисунке изображен график функции y f x производной функции f x определенной на интервале (-3:8) Найдите точку минимума


    Решение: Точки минимума соответствуют точкам смены знака производной с отрицательной на положительную. Когда изображен график производной, то производная отрицательная ниже оси Х. На заданном интервале она из отрицательной области в положительную (положительная - выше оси Х) переходит в точке 4 на оси Х. 4 - точка минимума.

<< < 345 6 7 > >>