график функции »
укажите, через какие из данных точек проходит график - страница 7
1) Функция задана формулой у= -2х+5. Принадлежат ли графику функции точки А(1;3) и В(-1;6).
2) Постройте график функции функции у=3х+4 и укажите координаты точек пересечения графика с осями координат.
3) Постройте график зависимости у=кх, если он проходит через точку А(2;-6). Найдите угловой коэффициент.
4) При каком значении параметра а графики функций у=5х + 3 и у=-4+(а+3) х параллельны?
5) Найдите точку пересечения графиков функций у=-1 и у=3х+2.
Решение: 1) у= -2х+5
А(1;3) - подставляем значение Х в уравнение системы
-2×1+5= -2+5 = 3
3=3 - сравниваем получившийся ответ со значением У, если ответы сошлись, точка принадлежит графику.
Ответ : принадлежит.
В(-1;6)
-2×(-1)+5=2+5=7
7≠3 - Естественно, если ответы не сошлись, то точка не принадлежит данному графику.
Ответ : не принадлежит
2) На фото
3) у=кх А(2;-6)
Чтобы найти К, подставляем значения Х и У
-6=К2
К= -3
Значит, уравнение будет у=-3х
Далее на фото
4 и 5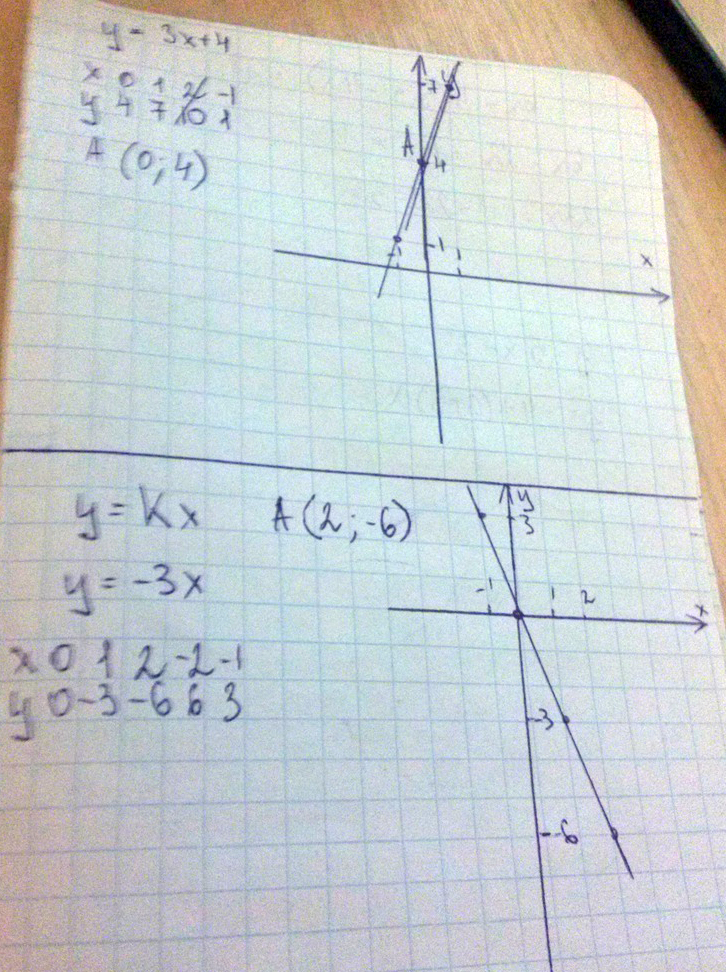
1) Функция задана формулой y=4x-30
Опредилите:
a) Значение y, если x= -2,5
б) Значение x, если y= -6
В) Проходит ли график функций через точку B (7:-3)?
2) Постройте график функий y=-3+3
Укажите с помошью графика, при каком значении x значение y ровно 6
3) В одной и той же системе координа постройте график функций y=0,5 и y= -4
4) Найдите координаты точки пересечения графиков функций y= -38x + 15 и y= -21x-36
5) Задайте формулой линейной функцией график который параллелен прямой y= -5x + 8 и проходит через начало координат.
Решение: Вообще функция это график, вместо Х ставим число - рассчитываем У.
Например Х=0, то У=4*0-30 = -30, то есть линия проходит через точку (0; -30).
Если Х=-2,5 то У=4*(-2,5)-30 = -40, значит линия проходит через точку (-2,5; -40).
Также можно подставить число на место У, тогда -6=4*Х-30, отсюда 4*Х=30-6, далее Х=(30-6)/4 = 6, то есть линия проходит через точку (6; -6).
Чтобы понять проходит линия через точку (7; -3) нужно подставить 7 вместо Х и посмотреть будет ли У равен -3. Попробуйте сами. Если что непонятно, спрашивайте )график функции y=(x-2)^2 а) Определите координаты вершины параболы. б) запишите уравнение оси симметрии параболы. г) Укажите, какие значения может принемать y. д) Как изменяется y, если аргумент x изменяется от минус бесконечности до 2, от 2 до плюс бесконечности. е) При каком x принемает наименьшее значение? Принимает ли функция наибольшее значение? ж) в каких точках график функции пересекает ось 0x? ось 0y? ,
Решение: а) (2; 0)б) y=(x-2)^2=x^2-4x+4
x=4/2=2
x=2
г) $$ [0;\ +\infty) $$
д) $$ (0;\ +\infty) $$
е) x=2
Нет
ж) С осью Ox: y=0
(x-2)^2=0
x=2
(2; 0)
С осью Oy: x=0
y=(0-2)^2=4
(0; 4)
y=(x-2)^2=x^2-4x+4. b=-4, a=1
а)$$ x_{0}=\frac{-b}{2a} \\ x_{0}=8 \\ y_{0}=36 $$
Цена товара сначала была повышена на 6% а затем новая цена снижена на 10% Как изменилась первоначальная цена товара?
Решение: Обозначим, для определенности, первоначальную цену товара через у. Первоначальная цена в процентах — всегда 100%. Поскольку сначала цену повысили на 6%, то новая цена в процентах равна 100+6= 106%. Нам надо эту новую цену выразить через старую цену у. Пусть х- новая цена товара. Условие оформляем как при решении задач на проценты с помощью пропорции:
у - 100%
х - 106%
Составим пропорцию и решим ее:
у:100=х:106
х=106*у:100
х=1,06у
2) Переходим ко второму изменению цены. Теперь 100% — это 1,06у. Эту цену снизили на 10%, значит, новая цена 100-10=90%. Выразим новую цену через у. Пусть х — новая цена товара.
1,06-100%
х-90%
1,06у:100=х:90
х=1,06у*90/100
х=0,954у
Таким образом, после второго изменения цена стала равной 0,954у.
3) Осталось выяснить, как изменилась цена по сравнению с первоначальной. Начальная цена у= 1∙у=100%у. Конечная цена 0,954у=95,4%у. Значит, цена уменьшилась на 100-95,4=4,6%.
ИЛИ ПРОЩЕ:
Первое изменение цены:
100%+6%=106%;
Второе изменение цены:
106%-10%=95,4%
Цена изменилась на:
100%-95,4%=4,6%
Ответ: Цена уменьшилась на 4,6%.Найдите наименьшее положительное число х, обладающее следующими свойствами: а) Х равен дроби, числитель и знаменатель которой - двузначные числа; б) если числитель этой дроби уменьшить на единицу, а знаменатель удвоить, то дробь станет равной 1/11; В ответе укажите сумму числителя и знаменателя полученной дроби Х без пробелов и каких-либо знаков препинания, например 100.
Решение: Можно действовать перебором. Числитель не может быть меньше 10 (т. к. двузначный). Если он 10, то после вычитания станет 9, тогда знаменатель должен стать (после удвоения) 99 (чтобы дробь стала быть равной 1/11). Но никакое целое число после удвоения не равно 99, значит 10 в качестве числителя не подходит. Берём 11. После вычитания 1 станет 10. Значит знаменатель станет 110 (опять чтобы получилось 1/11) Чтобы он (знаменатель) стал 110, первоначально он должен быть 55. Т. е. дробь 11/55 нам подходит, т. к. после преобразований она становится 10/110 = 1/11. Рассуждая дальше, найдём ещё такие числа, например 13/66 - тоже подходит, и оно меньше, чем 11/55, дальше 15/77 и оно ещё меньше, 17/88 - следующее и 19/99 - последнее, т. к. дальше пойдут трёхзначные знаменатели. И эта последняя дробь наименьшая из всех. Значит она и есть ответ. И сумма числителя и знаменателя 118
А) Эта дробь выглядит так: $$ \frac{2}{5,5} $$
б) Проверка: действительно, если уменьшить числитель на 1, а знаменатель удвоить, то получится $$ \frac{1}{11} $$
Сумма числителя и знаменателя полученной дроби равна: 2 + 5,5 = 7,5
Если указывать без знаков, тогда 75.
Ответ: 75

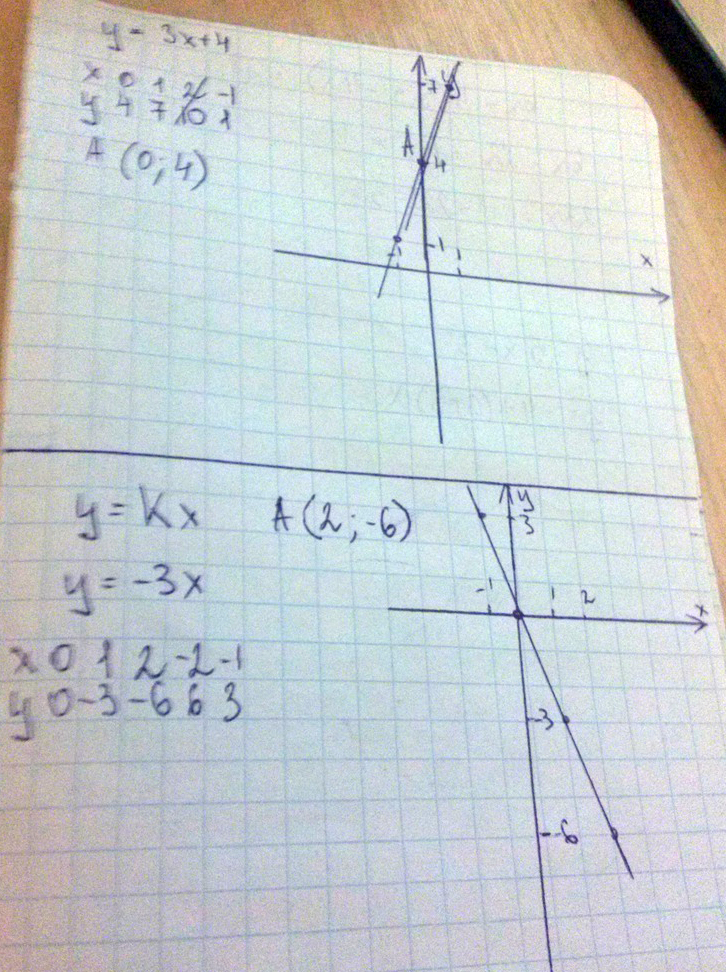
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...