укажите, через какие из данных точек проходит график - страница 5

Отметьте на координатной прямой точки: A(-3), B(0,5), C(-1,5), D(-1 3/4).
Ответьте на вопросы:
а) Какая точка имеет наибольшую координату?
б) Координата какой из точек имеет наибольший модуль? наименьший модуль?
в) Как изменяться координаты точек, если начало координат перенести на 4 единичных отрезка влево? Как изменятся их модули? Укажите точку, модуль координат которой не изменится.

Решение: ->x
D. A. C. B.
(-3,25)(-3)(-1,5)(0,5)
1. B - 0,5
2. Больший D - 3,25
Меньший B - 0,5
3.
Влево на 4
->x
D. A. C. B.
(-7,25)(-7)(-5,5)(-3,5) - точки
7,25. 7. 5,5. 3.5 - модули
Точка, модуль которой не изменяется - фактически нету, так как мы переместили все точки (вот если бы была точка 2 и мы бы переместили её на 4 влево, то получили бы точку -2 и их модули были равны), так что ПОСЛЕ ИЗМЕНЕНИЯ модули координат изменились.
№1) дан многочлен р(у)=2у²+4у+3. Найдите р(2)

№2) укажите уравнение, которое является математической моделью данной ситуации, если х км/ч - собственная скорость катера : "катер плывет по реке, скорость течения которой равна 2 км/ч, и за 4 ч по течению реки проплывает такое же расстояние, как и за 5 ч против течения".

а)4(х-2)=5(+2) в)4(2-х)=5(2+х)

б)4(х+2)=5(х-2) г)4(2+х)=5(2-х)

решите это уравнение и составьте математическую модель или наоборот

№3) одну пару противоположных сторон квадрата уменьшили на 8 см каждую, а другую пару увеличили на 3 см каждую. в результате получили прямоугольник, площадь которого на 79см² меньше, чем площадь квадрата. Найдите перимтр квадрата.

№4) докажите, что ab - cd >0 при всех значениях х, если а=х¹⁰+10, b=x²⁰-10x+100, c=x¹⁵-15, d=x¹⁵+15

Решение: 1) Подставим в формулу вместо х число 2

p(2)=2*2^2+4*2+3=19

2) х+2 это скорость по течению

х-2 это скорость против течения

4*(х+2) путь по течению

5(х-2) путь против течения

Значит верный ответ б)

3) Площадь квадрата Sкв=f^2

Площадь прямоугольника Sпр=(x-8)*(x+3)

x^2=(x-8)*(x+3)+79

x^2=x^2-5x-24+79

x^2-x^2+5x+24-79=0

5x=55

x=11

Периметр P=4*11=44

4)(x^10+10)*(x^20-10*x^10+100)-(x^15-15)*(x^15+15)

Первые два множителя это сумма кубов

Вторые два множителя это разность квадратов

(x^10+10)*(x^20-10*x^10+100)-(x^15-15)*(x^15+15)=(х^30+1000)*(x^30-255)>0

Так, как уменьшаемое больше вычитамого
Х-множество натуральных чисел. Указаны два свойства.
1 св-во:"быть целым числом"
2св-во:"быть рациональным числом"
На какие классы произошло разбиение множества Х. Укажите их.

Решение: Натуральные числа - это числа, возникающие естественным образом при счете, например 1,2,3. и т. д.
Целые числа - это расширение множества натуральных чисел N, получаемое добавлением к N нуля и отрицательных чисел вида -n (такие же, как натуральные, но с минусом).
Все ли натуральные числа обладают свойством: быть целым числом? Да. Это видно из определения. Значит, подмножество Х1, выделенное из множества Х при помощи свойства "быть целым числом", равно множеству Х.
Рациональные числа - это числа, представляемые обыкновенной дробью $$ \frac{m}{n} $$, где числитель m - целое число, а знаменатель n - натуральное число.
Все ли натуральные числа обладают свойством: быть рациональным числом? Да. Потому что любое натуральное число х можно представить в виде дроби $$ \frac{x}{1} $$. Значит, подмножество Х2, выделенное из множества Х при помощи свойства "быть рациональным числом", равно множеству Х.
Таким образом, все элементы множества Х удовлетворяют каждому из свойств 1 и 2, значит, множество Х разбивается на I класс - класс натуральных чисел, одновременно целых и рациональных.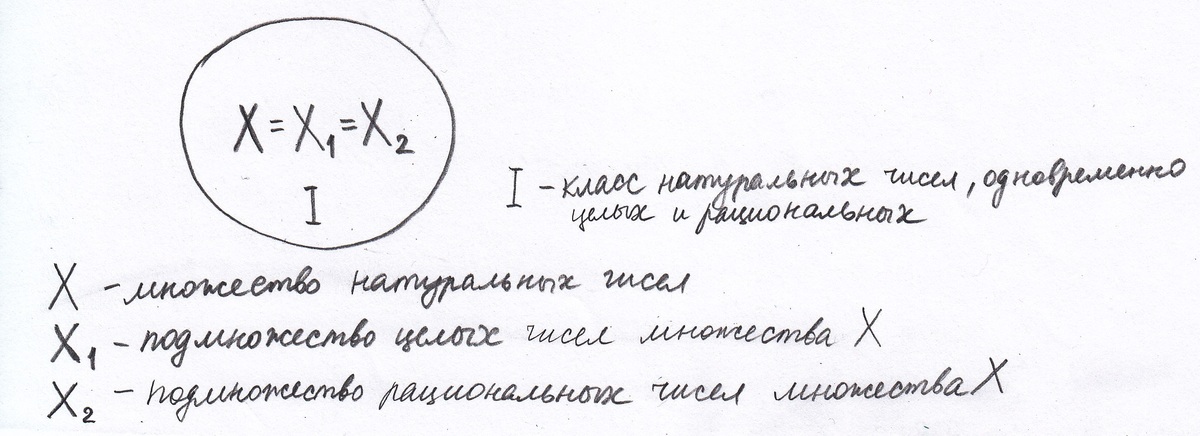
Рациональные и иррациональные числа
Укажите три каких-либо значения b, при которых значения выражения $ \sqrt{3b-1} $ является:
а) Рациональным числом;
б) Иррациональным числом

Решение: √(3b -1)
a) если корень извлекается, то данное число - рациональное
b =17/3; b = 26/3; b = 50/3
√(3·17/3 -1)=√(17 -1) = √16 = 4
√(3·26/3 -1) = √(26-1)=√25 = 5
√(3·50/3 -1) =√(50-1) =√49 = 7
б) если корень не извлекается, то данное число - иррациональное
b = 2; b = 3; b= 4
√(3·2-1) =·5
√(3·3-1) =√8
√(3·4-1) =√11

$$ \sqrt{3b-1}\\\\a) \sqrt{4}=2 \in Q\\3b-1=4\\3b=5\\b=5/3=1 \frac{2}{3} \\\\ \sqrt{9}=3\in Q\\3b-1=9\\3b=10\\b=10/3=3 \frac{1}{3}\\\\ \sqrt{16}=4\in Q\\3b-1=16\\3b=17\\b=17/3=5 \frac{2}{3} \\\\b)) b=1\\\sqrt{3*1-1}= \sqrt{2}\in I\\\\b=2\\ \sqrt{3*2-1}= \sqrt{5}\in I\\\\b=3\\ \sqrt{3*3-1}= \sqrt{8}=2 \sqrt{2}\in I $$
Укажите, какие из данных бесконечных десятичных дробей выражают рациональные числа, какие-иррациональные:
1) 0,010101.
2) 3,75121212.
3) 0,010010001.
4) 3,7512412441244412444441.
5) 5,43171717.
6) 1,41421.
7) n=3,14159265358.
8) 1,7320.

Решение: 1) 0,01010101.=0,0(10) - рациональное число.
2) 3,75121212.=3,75(12) - рациональное число.
3) 0,0100110001. иррациональное число.
4) 3,75124124412444441 - иррациональное число.
5) 5,43171717.=5,43(17) - рациональное число.
6) 1,141421. иррациональное число.
7) π=3,14159265358. иррациональное число.
8) 1,7320. иррациональное число.

5,43171717.=5,43(17) - бесконечная периодическая дробь, значит это рациональное число.
0,01001000100001000001. иррациональное число, т. к. дробь не периодическая
3,7612412441244412444441. иррациональное число
(это, если вы забыли написать многоточие, а оно на самом деле в условии есть). Если многоточия нет, то дробь десятичная конечна и тогда это рациональное число.
1,41421 - это конечная десятичная дробь, значит число рациональное
1,7320 - конечная десятичная дробь, значит число рациональное
P.S. Если в конце дробей не стоит многоточия, то все дроби конечны и значит числа рациональны все.
1,41421. иррациональное
1,7320. иррациональное

<< < 3 45 6 7 > >>