график функции »

найдите координату точек пересечения графика функции - страница 20

  • Найдите координаты всех точек пересечения графиков функций
    y=x^2-3x+5 и y=21+x-x^2


    Решение: y=x^2-3x+5 и y=21+x-x^2
    приравниваем обе части: x^2-3x+5= 21+x-x^2
      х^2+x^2-3x-x=21-5

                                            2x^2-4x=16

    переносим 16 и получаем квадратное уравнение:        2x^2-4x-16=0

    можно сократить на 2: x^2-2x-8=0

    решаем кв. уравнение, найдем дискриминант уравнения по формуле:

                                                                                           D=b^2-4ac

                                                                                           D=(-2)^2-4*1(-8)=4+32=36

    находим корни уравнения по формуле: x1=(-b-(корень из D))/2a 

                                                                 х1=(2-6)/2*1=-4/2=-2
                                            х2= (-b+(корень из D))/2a 

                                                                x2=(2+6)/2*1=8/2=4

                                                              

    подставим корни уравнения в любую из графиков функции и получим координаты точек пересечения. Возьмем точки А и B, точка А имеет координату (-2;15), B(4;9)

  • Найдите координаты точек пересечение графиков функций y=-0.5x в квадрате + 2,5 и y=2x в квадрате+5x


    Решение: Заранее
    D=b^2-4ac
    X=(-b+-кореньD)/2a

    Есть общая у сопоставим их

    -0,5х^2+2.5=2x^2+5x

    Переносим в одну сторону

     -0,5х^2+2.5-2x^2-5x=0

     -2,5х^2-5x+2,5=0 

    Через дискриминант

    D=50

    X1=(-5+корень 50)2*2,5=0,4

    X2= (-5-корень 50)2*2,5=-2,4

    Координаты точек пересечения х1 и х2 

    . 

  • Найдите произведение координат точек пересечения графиков функций y=√x+1 и y=2\x.


    Решение: Точек пересечения будет всего одна - в 1 четверти, в которой расположен график первого уравнения.
    √x+1 =2/x
    √x=(2/x)-1
    x=((2/x)-1)²
    х = (4-4х+х²) / х²
    Приводим к общему знаменателю:
    х³ = 4-4х+х²
    х³-х²+4х-4 = 0
    х²(х-1)+4(х-1) = 0
    (х²+4)(х-1) = 0.
    Первый множитель не может быть равен 0, поэтому:
    х - 1 = 0
    х = 1 у = 2/1 = 2 это координаты точки пересечения графиков заданных функций.
    Их произведение равно 2*1 = 2.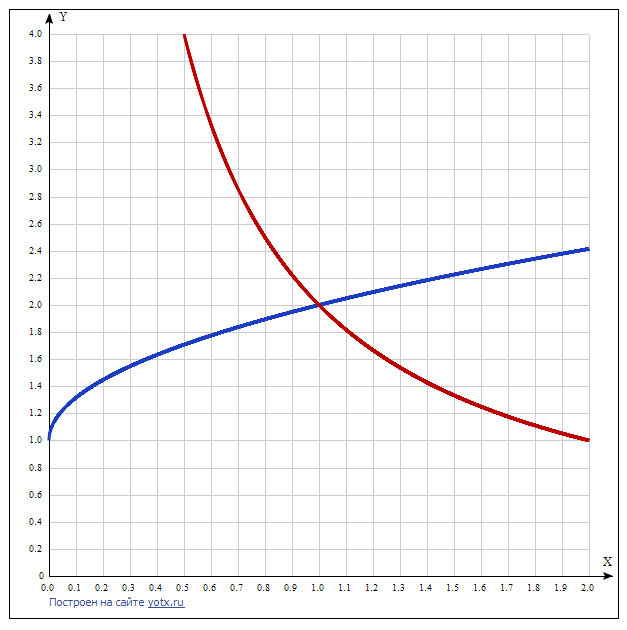

    Точек пересечения будет всего одна - в четверти в которой расположен график первого уравнения. x x x x - x x - х - х х х Приводим к общему знаменателю х - х х х -х х-     х х...

  • Не выполняя построения, найдите координаты точек пересечения с осями координат графиком функции
    а) y = - 2,4x+ 9,6
    б) y = - 0,7x +- 28


    Решение: а) y=-2,4x+9,6

    при х=0

    y=9,6

    координаты точки пересечения с осью X - (0; 9,6)

    при y=0

    x=9,6/2,4=4

    координаты точки пересечения с осью Y - (4: 0)

    б) y=-0,7x-28

    при х=0

    y=-28

    координаты точки пересечения с осью Х - (0,28)

    при у=0

    x=-40

    координаты точки пересечения с осью У - (-40;0)

  • На координатной прямой отмечены точки X(-18) и Y(24). Найдите координаты точек M и N, делящих отрезок XY на три равные части.(с вычислениями)


    Решение: Отрезок XY равен 24+18=42. Если разделить его на три равные части, то каждая часть будет равна 42/3=14. Значит, отрезки XM,MN,NY, каждый из которых - третья часть исходного отрезка, также будут равны 14. Точка M находится правее точки X, значит, её координата равна -18+14=-4. Аналогично, точка N левее точки Y и её координата равна 24-14=10.
    Ответ: М(-4), N(10). 

<< < 181920 21 22 > >>