график функции »
найдите координату точек пересечения графика функции - страница 21
На координатной прямой отмечены точки А(x-3) и В(3x+5). Длина отрезка АВ равна 10. Найдите координаты точек А и В.
Решение: 1. Точка А левее точки В, то есть координата точки В больше координаты точки А. Составим и решим уравнение: 4х-3=2х+1-2 из уравнения найдём, что х=1, тогда координаты точек: А(1), В(3).
2. Точка А правее точки В, то есть координата точки В меньше координаты точки А. Составим и решим уравнение: 4х-3=2х+1+2 из уравнения найдём, что х=3, тогда координаты точек: А(9), В(7).На координатной прямой отмечены точки А(-5) иВ(3). Точки C,D, и E делят отрезок АВ на равные отрезки АС, CD, DE и ЕВ. Найдите координаты точек C, D и Е
Решение: Длина AB 3- (-5) = 8
значит длина каждого из отрезков AC, CD, DE и EB равна двум.
значит координата точек следующая:
С(-3)
D(-1)
E(1)Смотри вложение ниже:
С(-3), D(-1), E(1)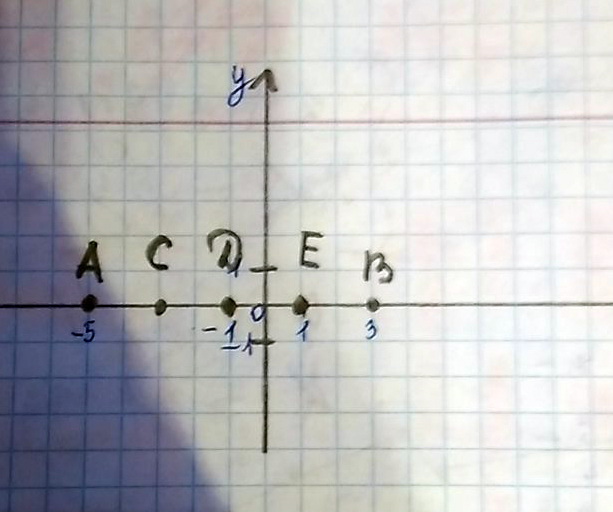
На координатной прямой отмечены точки А(-5) и В(3). Точки С D и E делят отрезок АВ на равные отрезки АС СD DE EВ. Найдите координаты точек С D
E
Решение: Найдем длину отрезка AB: от координаты конца отнимем координату начала, возьмем по модулю
-5-3 = |-8| = 8
Найдем длину отрезков AC CD DE EB, по условию они равны
8:4 = 2
Теперь к координате А прибавляем по 2 и получаем координаты нужные нам:
-5+2 = -3
С(-3)
-3+2 =-1
D(-1)
-1+2 = 1
Е(1)На координатной прямой отмечены точки A(4x-3) и B(2x+1). Длина отрезка AB равна 2. Найдите координаты точек A и B. Рассмотрите два случая.
Решение: 1. Точка А левее точки В, то есть координата точки В больше координаты точки А. Составим и решим уравнение: 4х-3=2х+1-2 из уравнения найдём, что х=1, тогда координаты точек: А(1), В(3).
2. Точка А правее точки В, то есть координата точки В меньше координаты точки А. Составим и решим уравнение: 4х-3=2х+1+2 из уравнения найдём, что х=3, тогда координаты точек: А(9), В(7).
Расстояние между точками = модуль разности координат этих точек
$$ |AB|=|4x-3-(2x+1)|=|4x-3-2x-1|=|2x-4| $$
по условию известно, что
$$ |AB|=2 $$
значит надо решить уравнение:
$$ |2x-4|=2, \\ \\ 2x-4=-2 $$ или $$ 2x-4=2 $$
$$ x_{1}=1 ; x_{2}=3 \\ A_{1}(4*1-3);B_{1}(2*1+1) \\ A_{2}(4*3-3);B_{2}(2*3+1) \\ A_{1}(1);B_{1}(3) \\ A_{2}(9);B_{2}(7) \\ $$
Ответ:$$ A_{1}(1),B_{1}(3); A_{2}(9),B_{2}(7) \\ $$Постройте на координатной плоскости прямую проходящую через точки M(1;1) N(-1;3).
Найдите координаты точек прямой с осями Оx и Оy.
Решение: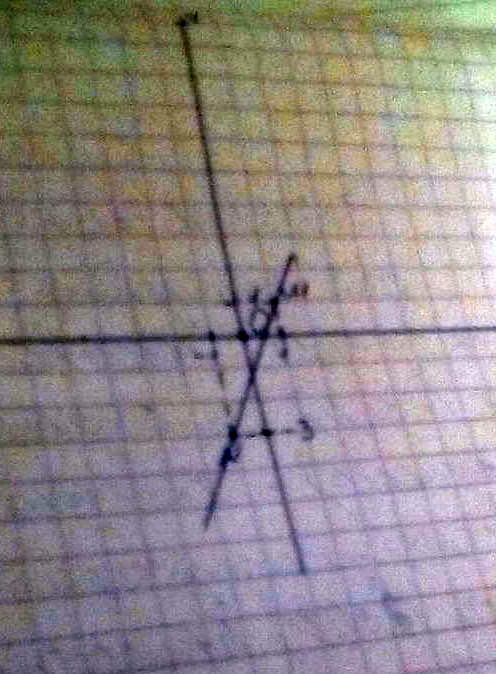

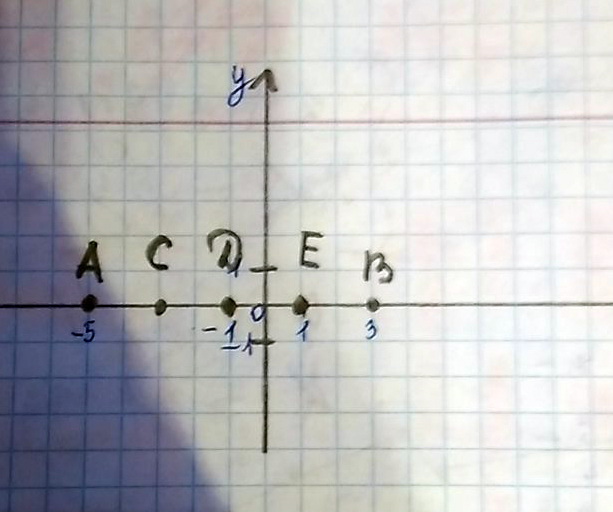
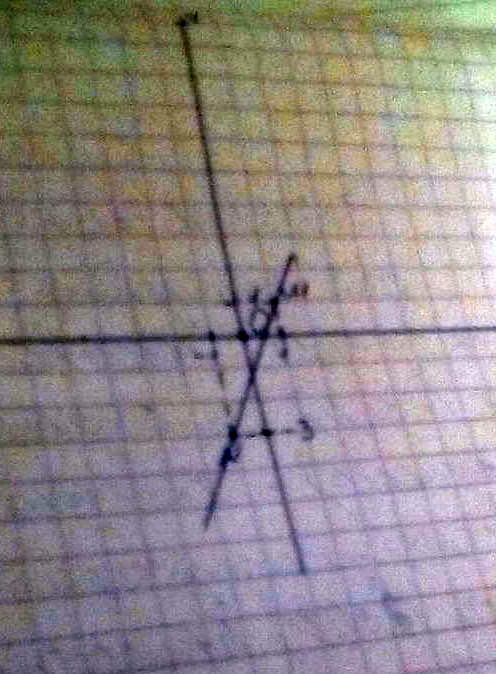
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...