график функции »
найдите координату точек пересечения графика функции - страница 23
Отметьте на координатной прямой точки А(-4) и В(2); отметьте точки С и D такие, что точки A и B делят отрезок на равные части. Найдите координаты точек C и D.
Решение:
-4 -1 0 2 5
|-|
A A B B
варианты комбинаций А и В:
1. А(-4), В(2);
2. А(-4), В(5);
3. А(-1), В(2);
4. А(-1), В(5).
промежутки между А и В:
1. 6
2. 9
3. 3
4. 6
варианты точек C, D:
1. С(-10), D(8);
2. С(-13), D(14);
3. С(-4), D(5);
4. С(-7), D(11);
Длинна единичного отрезка на координатной прямой равна 1 см. Длина отрезка CD равна 16см. Середина отрезка изображается точкой с координатой -5. Найдите координаты точек C и D?
Решение: Отрезок СD=16см, значит половина отрезка равна 8см или 8 единичных отрезков. (-8 ед. отрезков влево от середины на координатной прямой и
8 ед. отрезков вправо от середины на координатной прямой).
Середина отрезка находится в точке -5.
Тогда координаты концов отрезка будут:
С(-5+(-8)) или С(-13) и D(-5+8) или D(3).

На координатной прямой отмечены точки A(x-3) и B(3x+5). Длина отрезка AB равна 10. Найдите координаты точек A и B.
И уравнение 3*(4x-5)-(7x+1)=-19,5
Решение: Длина отрезка АВ
B-A = 3x+5 - (x-3) = 10
3x+5 -x+3 =10
2x =10-8 = 2
x = 1
Координаты точек - А(-2) В(8) - расстояние =10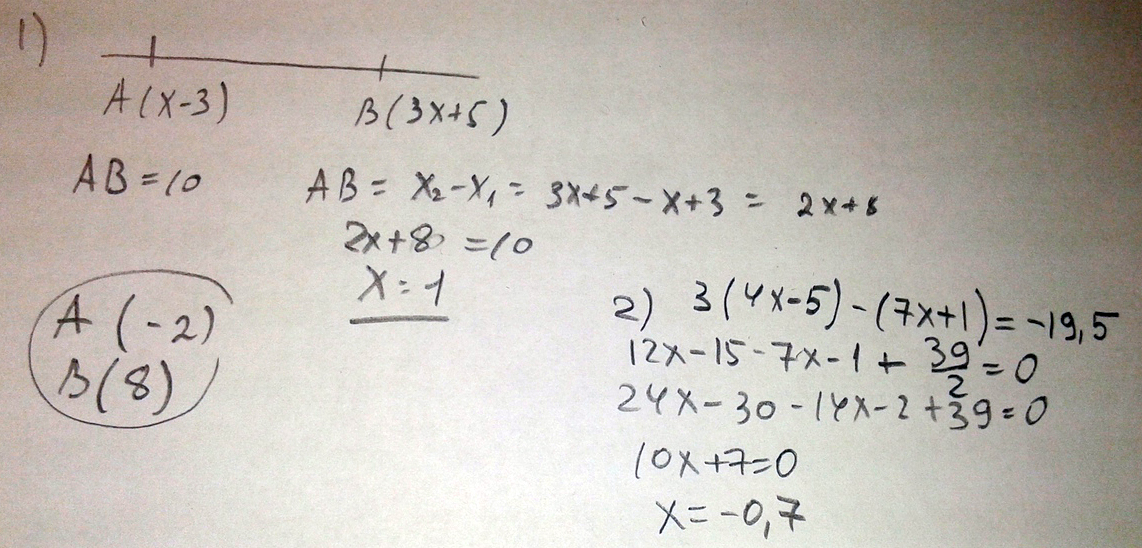
1) Длина единичного отрезка на координатной прямой равна 1 см. Точке A соответствует число -2,5, а точке B соответствует число, ему противоположное. Найдите длину отрезка AB.
2) Длина единичного отрезка на координатной прямой равна 1 см. Длина отрезка CD равна 16 см. Середина отрезка изображается точкой с координатной -5. Найдите координаты точек C и D.
Решение: 1) Число, противоположное (-2,5) — это, очевидно, (2,5), тогда от А до (0) и от (0) до В — 2 раза по 2,5 единиц, что даёт нам длину отрезка АВ=2*2,5= 5 см.
2) Если середина отрезка CD имеет координату (-5), то края отрезка будут находиться слева и справа от этой точки на расстояниях половины общей длины отрезка CD 16/2=8 cm, а координаты точек будут: для С - (-5)+(-8)=(-13); для D - (-5)+(8) = (3). Ответ: С(-13); D(3).На координатной плоскости начертите прямую проходящую через точки А (-2;-1) В(3;1,5) отметьте на прямой АВ точки, абсциссы которых соответственно равны -1,0,1,2 найдите координаты этих точек "
Решение: Прямая, проходящая через точки А (-2;-1) В(3;1,5) имеет уравнение:$$ \frac{x+2}{3+2} = \frac{y+1}{1,5+1} \\ \frac{x+2}{5} = \frac{y+1}{2,5} $$.
Числитель и знаменатель правой дроби умножим на 2 и получим уравнение: х + 2 = 2у + 2.
Уравнение прямой: у = (1/2) х.
Прямая проходит через начало координат.
Теперь подставляем абсциссы заданных точек в полученное уравнение прямой и находим соответствующие ординаты.
х = -1, 0, 1, 2
у = -1/2, 0, 1/2, 1.


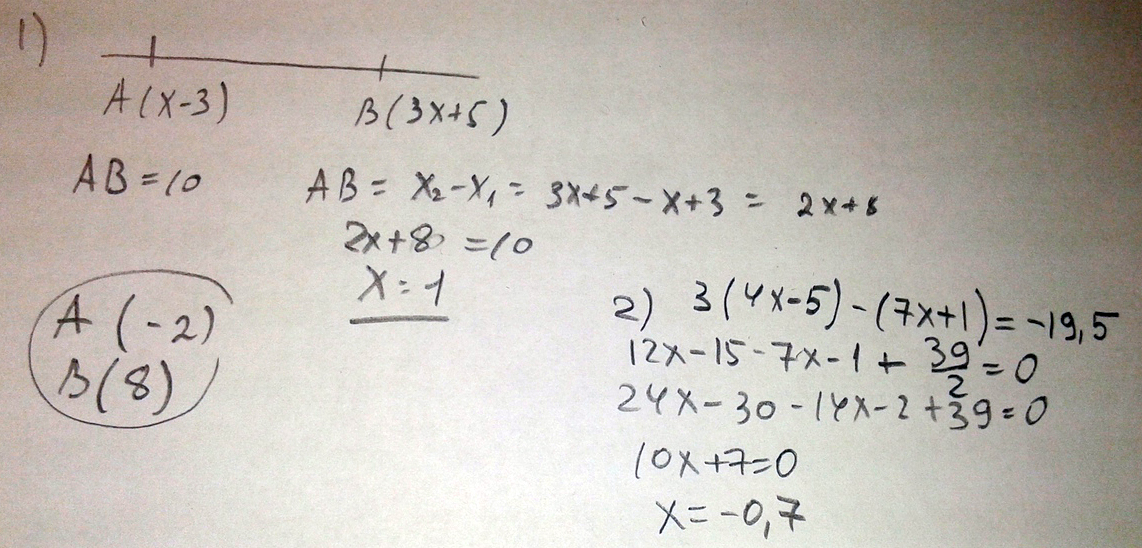
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...