график функции »

найдите координату точек пересечения графика функции - страница 24

  • Расположите точки A, C, S, M на координатной прямой так, чтобы координаты точек A, C были положительными целыми числами, координата точки S являлась отрицательным числом и лежала на расстоянии 4 единичных отрезков от точки А и на расстоянии 8 единичных отрезков от точки М, значение координаты точки М на 2 единицы меньше значения координаты точки С, а координаты всех точек не превышали значение 8. Найдите сумму значений координат искомых точек.


    Решение: Так как координата точки S принимает отриц. значение, то предположим, что S имеет координату -3.
    тогда точка А имеет координату -3+4=1, что согласуется с условием, согласно которому А имеет положительную координату.
    Точка M имеет координату -3+8=5; точка С координату 5+2=7. Точка S не может иметь другую координату, так как если она примет значение, меньшее -3, координата точки А станет не положительным( равным нулю или меньше), если же координата точки S больше -3, то координата точки С выходит за предел, равный 8. Сумма всех координат : -3+1+5+7=10

  • найдите два решения данных неравенств
    4х - у² ≥ 1
    Координаты каких точек являются решением неравенства у≦ -х2+81
    А(4:-2) В(9:0) С(-10:1) Д(11:-11)
    На координатной плоскости изобразите штриховкой решения неравенства
    х2+у2≥4
    На координатной плоскости изобразите штриховкой решение неравенства
    х2+у2≦2,25


    Решение: 1
    y²≤4x-1
    Ответ (2;2)  (3;3)
    2
    у≦ -х2+81
    А(4:-2)  -2≤-16+85⇒-2≤69 является
    В(9:0)  0≤-81+81⇒0≤0  является
    С(-10:1)  1≤-100+81⇒-1≤-19 не является
    Д(11:-11)  -11≤-121+81⇒-11≤-40  не является
    3
    х2+у2≥4
    Решением будет внешняя область круга радиусом 2
    4
    х2+у2≦2,25
    Решением будет внутренняя область круга радиусом 1,5

    y x- Ответ   у -х А -   - - - являетсяВ   -   является С -   - - - не являетсяД -   - - - -   не является х у Решением будет внешняя область круга радиусом х у Решением будет...

  • Диагонали прямоугольника ABCD пересекаются в начале прямоугольной системы координат. Найдите координаты точек A,B,C, если точка D имеет координаты (-3,2) и стороны прямоугольника параллельны осям координат.


    Решение: Решение .
    Так точка пересечения диагоналей в начале системы координат, то координаты вершин будут симметричны.
    D(-3;2) превращается в B(3;-2) и в A(-3;-2) и C(3;2)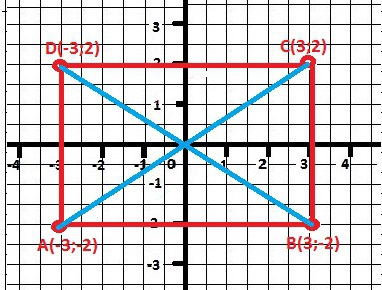

    Решение .Так точка пересечения диагоналей в начале системы координат то координаты вершин будут симметричны.D - превращается в B - и в A - - и C...

  • На координатном луче с единичным отрезком длиной 5 см заданы точки А(х) В(х-4/5) С(х+4/5) где х=1целая 2/5 Найдите координаты точек В и С


    Решение: Координаты точек находятся суммированием координат точек.
    В = А - 4/5 = 3/5 - пишем - B(3/5) - ОТВЕТ
    С = А + 4/5 = 2 1/5 - С(2 1/5) - ОТВЕТ
    Рисунок прилагается.

    Координаты точек находятся суммированием координат точек.В А - - пишем - B - ОТВЕТС А - С - ОТВЕТРисунок прилагается....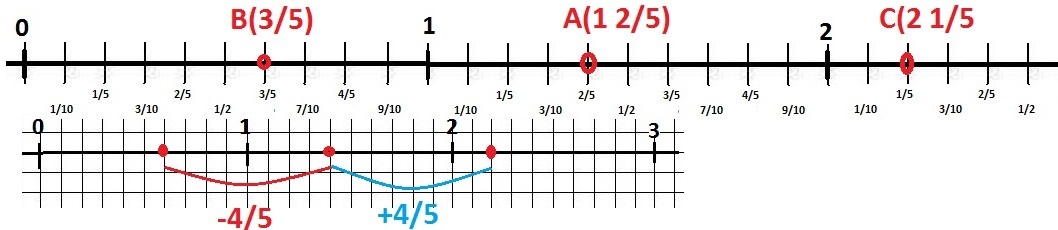

  • Середины M и N отрезков АВ и ВС, расположенных на координатном луче, имеют координаты 152 и 402 соответственно. Найдите координаты точек А, В, С, учитывая, что отрезок АВ состоит из двух долей, а отрезок ВС из трех таких же долей. Решить задачу без х и уравнения.


    Решение: т. к М-середина АВ, а N-середина ВС=1,5доли, то от точкиN до точки М будет расстояние 2,5 доли, т. е 

    (402-152):2,5=100-это будет 1 доля отрезка

     т. к ВN=ВС, АМ=МВ, то 

    402+100*1,5=552- точка(С)

    402-100*1,5=252- точка(В)

    152-100=52- точка(А)

    Если отрезок АВ=2 доли, а отрезок ВС=3 такие же доли, то отрезок АС=5 долей. Если точка М-середина отрезка АВ, а точка N-середина отрезка ВС, то отрезок MN=1/2 отрезка АС.

    402-152=250 длина отрезка MN

    250:5=50 1/2 доли

    50*2=100 целая доля

    152-100=52 координата точки А

    152+100=252 координата точки В

    100*3=300 длина отрезка ВС

    252+300=552 координата точки С

<< < 222324 25 26 > >>