промежутки возрастания и убывания функции - страница 3

Каждой параболе поставь в соответствие ее вершину: А) у = х2 + 6х Б) у = х2 + 6х + 9 В) у = 6х – х2 1) (3; 9) 2) (–3; 0) 3) (–3; –9) 2. Упрости выражение: а) (а – 3)(а + 3) – (2 – а)2; б) (2a + 3b)(3b – 2a) – (a – b)(b + a); в) (x – 2)(x + 2)(x – 3)(x + 3); г) (5 – a)2 – (а + 1)2 + 5(2 – a)(2 + a). 1. Найди площадь равнобедренного треугольника, основание которого равно 8, а боковая сторона 5. 1) 40 2) 18 3) 12 4) 24 3. Каждому квадратному трехчлену поставь в соответствие его разложение на множители: А) х2 – 3х + 2 Б) х2 – 2х – 3 В) 2х2 + х – 3 1) (х – 1 )(х – 2) 2) (х + 1)(х – 3) 3) (х – 1)(2х + 3) 2. Задачи: а) Найти периметр ромба, если длина его меньшей диагонали равна 7 см, а один из его углов равен 60. б) Диагональ параллелограмма делит его на два равносторонних треугольника. Докажи, что этот параллелограмм —ромб, и найди угол, который образует его большая диагональ со сторонами. Реши неравенство, изобрази на числовой прямой множество его решений и запиши ответ с помощью обозначений: 1) 12 + х > 18; 2) 6 – х  4; 3) 6 + х < 3 – 2х; 4) 4 + 12х > 7 + 13х; 5) 3(2 + х) > 4 – х; 6) –(4 – х)  2(3 + х); Реши уравнение: 1) | 2x – 3 | = 5; 2) | 2 + 7x | = 1; 3) | 5 – 3x | = 0; 4) | 2x + 4 | = –2. Реши неравенство: 1) | 3x + 4 |  2; 2) | 6 – x | > 3. 2. Из формулы у = kx + b выразите угловой коэффициент k. 3. Каждому квадратному уравнению А) х2 – 2х – 8 = 0, Б) 5х2 – 3х – 2 = 0, В) х2+ 6х + 9 = 0 поставьте в соответствие его корни 1) – 0,4; 1, 2) – 2; 4, 3) –3. 4. Вычислите периметр прямоугольника АВСD, если биссектриса угла В пересекает сторону АD в точке Е и делит ее на отрезки АЕ = 17 и ЕD = 21. 5. Постройте график функции у = х2 + 4х – 5 и укажите промежутки ее возрастания и убывания.

А) у = х² + 6х 3) (–3; –9)

Б) у = х² + 6х + 9 2) (–3; 0)

В) у = 6х – х²          1) (3; 9)

Упрости выражение:

а) (а – 3)(а + 3) – (2 – а)²=a²-9-4+4a-a²=4a-13;

б) (2a + 3b)(3b – 2a) – (a – b)(b + a)=9b²-4a²-a²+b²=10b²-5a²;

в) (x – 2)(x + 2)(x – 3)(x + 3)=(x²-4)(x²-9)=x⁴-13x²+36;

г) (5 – a)² – (а + 1)² + 5(2 – a)(2 + a)=25-10a-a²-a²-2a-1+20-5a²=-7a²-12a+44.

 Найди площадь равнобедренного треугольника, основание которого равно 8, а боковая сторона 5.

высота треугольника проведенная к основанию=3   (5*5-8/2 *8/2=9)

S=0.5*8*3=12

Ответ 3

Каждому квадратному трехчлену поставь в соответствие его разложение на множители:

А) х² – 3х + 2     1) (х – 1 )(х – 2)

Б) х² – 2х – 3     2) (х + 1)(х – 3)

В) 2х² + х – 3    3) (х – 1)(2х + 3)

Задачи:

а) Найти периметр ромба, если длина его меньшей диагонали равна 7 см, а один из его углов равен 60⁰.

меньшая диагональ=стороне ромба, т. к получается равносторонний треугольник, значит Р= 4*7=28

б) Диагональ параллелограмма делит его на два равносторонних треугольника. Докажи, что этот параллелограмм —ромб, и найди угол, который образует его большая диагональ со сторонами.

Равносторонние треугольники, значит углы по 60⁰. Каждая сторона равна диагонали, значит все стороны равны⇒ ромб. Угол=60⁰

Реши неравенство, изобрази на числовой прямой множество его решений и запиши ответ с помощью обозначений:

1) 12 + х > 18; х>6

2)

3) 6 + х < 3 – 2х;   3x<-3,   x<-1

4) 4 + 12х > 7 + 13х;  -x>3, x<-3

5) 3(2 + х) > 4 – х;  6+3x>4-x,  4x>-2,  x>0.5

6)

Реши уравнение:

1) | 2x – 3 | = 5; 2x-3=5,2x=8, x=4 и 2x-3=-5, 2x=-2, x=-1 Ответ -1; 4

2) | 2 + 7x | = 1; х=-1/7  и х=-3/7

3) | 5 – 3x | = 0;  х=5/3

4) | 2x + 4 | = –2. решений нет

Из формулы у = kx + b выразите угловой коэффициент k.

k=(y-b)/x

Каждому квадратному уравнению поставьте в соответствие его корни

А) х² – 2х – 8 = 0,      2) – 2; 4,

Б) 5х² – 3х – 2 = 0,    1) – 0,4; 1,

В) х²+ 6х + 9 = 0   3) –3.

Вычислите периметр прямоугольника АВСD, если биссектриса угла В пересекает сторону АD в точке Е и делит ее на отрезки АЕ = 17 и ЕD = 21.

AE=AB=17

AD=AE+ED=38

P=2*(17+38)=110

1, Постройте график функции y=x2- 3[x]-модуль +2 и найдите промежутки монотонности.
2. Найдите множество значений функции на промежутке x принадлежит [-1;2]
y=x2- 3[x]+2.
3. Постройте график функции y=2x+[x-1].

Постройте график функции y=x^2+4x-7. с помощью графика найдите:
1) значение функции, соответствующее значению аргумента, равному -1,5
2) значение аргумента, при котором значение функции равно -2
3) промежутки знакопостоянства функции
4) промежутки возрастания и убывания функции
5) область значений функции
6) координаты точки графика, симметричной относительно его оси симметрии точке с абсциссой, равной 5

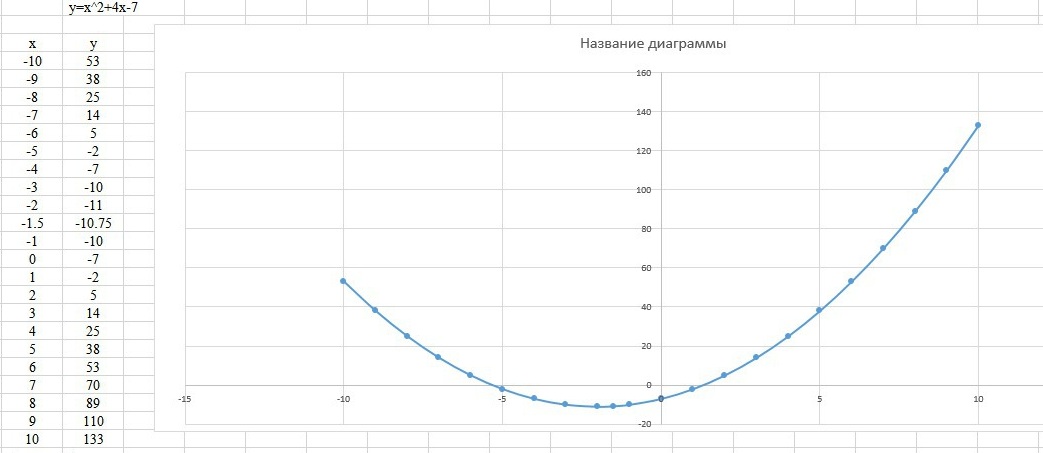
1. Найти координаты вершины параболы: а) у = х2 – 8х + 7; б) у = -х2 – 4х + 9; в) у = 2х2 + 16х – 1. 2. Постройте график функции у = -х2 + 6х – 5. Найдите по графику: а) нули функции; промежутки, в которых у > 0, у < 0; б) промежутки возрастания и убывания функции, наибольшее ее значение.

Дана функция y=3/4 x - 6. Найти координаты точек пересечения с осями. При каких значениях аргумента функция принимает положительные значения. Промежутки возрастания и убывания функции