график функции »

промежутки возрастания и убывания функции - страница 4

  • 241. Разложите на множители выражение (х+у)^2-x^4-y^4+2*x^2*y^2.
    242. Сократите дроби: 10а^2-6a+5ab-3b / 5a^2-8a+3
    x^2-4x+1 / x^2-2(2+V3)x+7+4V3
    259. Постройте график функции:
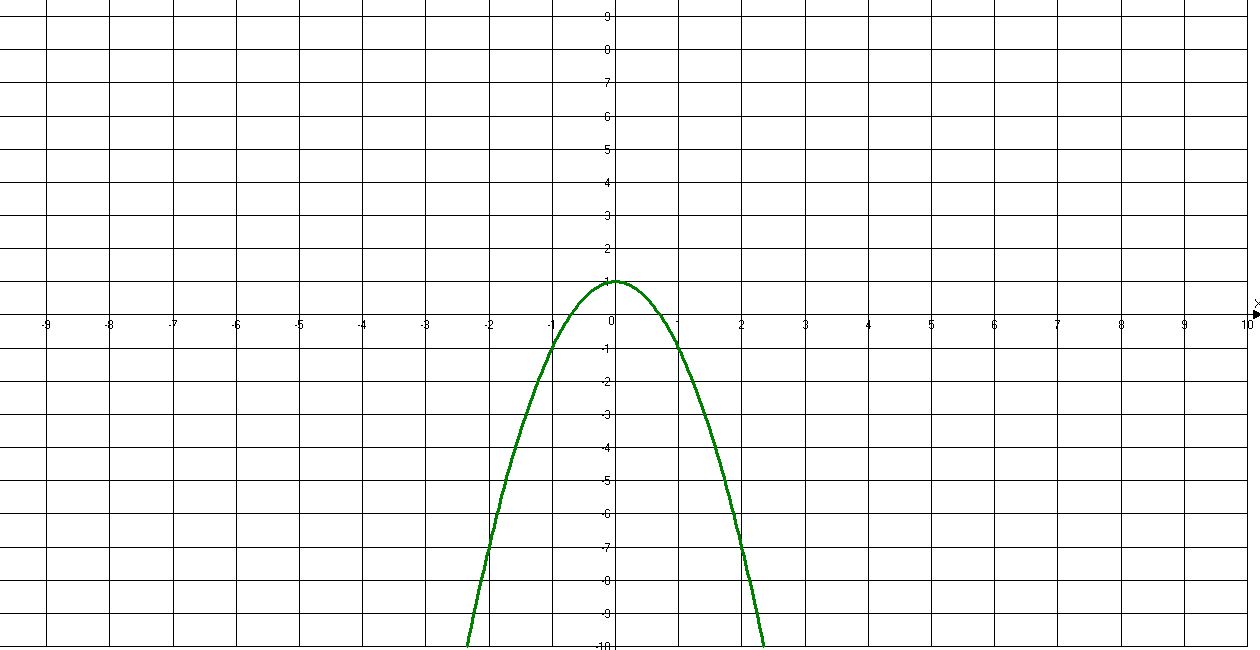
    у=-2х^2+1
    y=3(x+2,5)^2
    267. Найдите координаты вершины параболы и определите напраление ветви:
    у=х^2-4x+3
    y=x^2-10x+15
    270. Постройте график данной функции, используя алгоритм:
    у=2x^2-3x-2
    277. Постройте график функции: у=-3x^2-6x-4
    а) найти промежутки возрастания и убывания функции
    б) найти максимальное значение функции
    в) при каких х, у>0.


    Решение: 241. $$ (x+y)^2-x^4-y^4+2x^2y^2=(x+y)^2-(x^4+y^4-2x^2y^2)=\\ (x+y)^2-(x^2-y^2)^2=(x+y+x^2-y^2)(x+y-x^2+y^2)=\\((x+y)+(x-y)(x+y))(x+y-(y-x)(y+x))=\\ (x+y)(1+x-y)(x+y)(1-y+x) $$

    242. $$ \frac{10a^2-6a+5ab-3b}{5a^2-8a+3}=\frac{5a(2a+b)-3(2a+b)}{5(a-1)(a-0.6)}=\frac{(5a-3)(2a+b)}{(a-1)(5a-3)}=\frac{2a+b}{a-1} \\ \frac{x^2-4x+1}{ x^2-2(2+\sqrt3)x+7+4\sqrt3}=\frac{(2-\sqrt3)(2+\sqrt3)}{(2+\sqrt3)(2+\sqrt3)}=\frac{2-\sqrt3}{2+\sqrt3}=\frac{7-4\sqrt3}{1}=7-4\sqrt3 $$

    259. см вложение

    267. $$ y=-2x^2+1\\ n=\frac{-b}{2a}=\frac{0}{-4}=0\\ m=y(n)=0+1=1\\ O(0;1) $$

    ветви вниз

    $$ y=x^2-10x+15\\ n=\frac{-b}{2a}=\frac{10}{2}=5\\ m=y(n)=25-50+15=-10\\ O(5;-10) $$

    ветви вверх

    . x y -x -y x y x y - x y - x y x y - x -y x y x -y x y-x y x y x-y x y x y- y-x y x x y x-y x y -y x . frac a - a ab- b a - a frac a a b - a b a- a- . frac a- a b a- a- frac...

  • Исследовать функцию y=1/3x^3-2x^2+4x+1 найти промежутки монотонности и координаты точек экстремма


    Решение: Дана функция y=(1/3)x^3-2x^2+4x+1.
    Производная равна (1/3)*3х² - 2*2х + 4 = х² - 4х + 4.
    Находим критические точки, приравняв производную нулю:
    х² - 4х + 4 = 0.
    Квадратное уравнение, решаем относительно x: 
    Ищем дискриминант:D=(-4)^2-4*1*4=16-4*4=16-16=0; 
    Дискриминант равен 0, уравнение имеет 1 корень:x=-(-4/(2*1))=-(-2)=2. 
    Исследуем поведение производной вблизи критической точки.
    х =   1.5  2  2.5
    у’ =x^2-4x+4  0.25 0   0.25.
    Производная не меняет знак - значит, нет экстремума.
    Так как производная положительна, то функция на всём числовом промежутке возрастающая.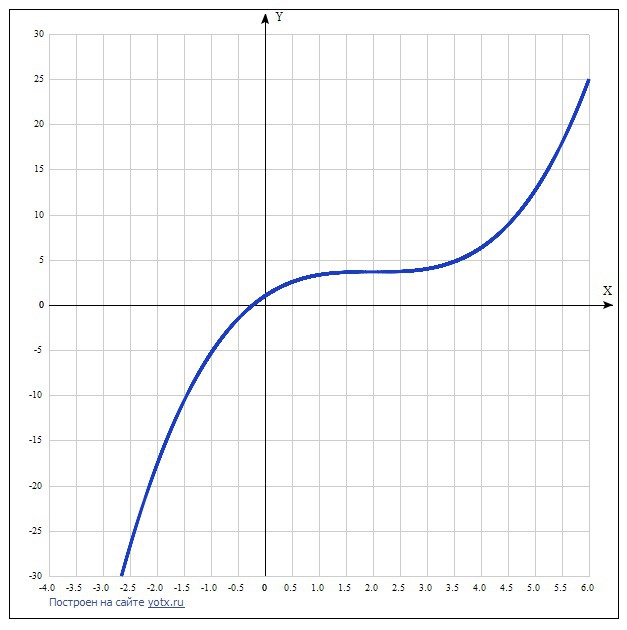

    Дана функция y x - x x .Производная равна х - х х - х .Находим критические точки приравняв производную нулю х - х .Квадратное уравнение решаем относительно x  Ищем дискримина...

  • Построить график функции по плану:
    1) Найти ООФ
    2) Если есть точки разрыва, исследовать их
    3) Найти точки пересечения с осями координат
    4) Вычислить чётность/нечётность
    5) Выяснить периодичность
    6) Найти производную, промежутки монотонности функции, экстремумы
    7) Найти промежутки выпуклости, вогнутости, вторую производную и точки перегиба
    8) Асимптоты графика функции (y=kx+b)
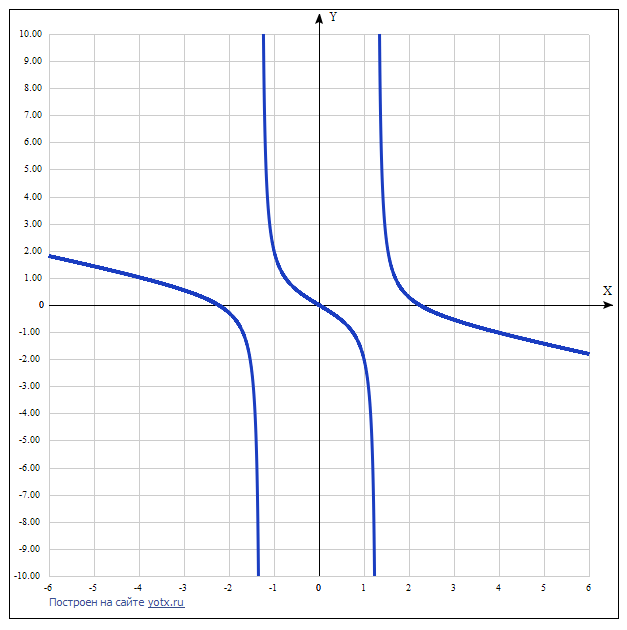
    9) Построить график\( y=(x^3-5x)/(5-3x^2) \)


    Решение: 1) Найти ООФ 
    2) Если есть точки разрыва, исследовать их
    Эти 2 вопроса практически совпадают, так как ООФ включает точки разрыва:
    Если переменная в знаменателе, то есть точки разрыва при знаменателе, равном 0.
    5 - 3х² = 0,
    х = +-√(5/3),
    значит, точки разрыва х₁ = -√(5/3) =  -1.290994, х₂ = √(5/3) = 1.290994.
    То есть график функции разбит на 3 участка:
     первый от-∞ до -√(5/3),
    второй от-√(5/3) до √(5/3),
    третий от √(5/3) до +∞.
    3) Найти точки пересечения с осями координат:
    С осью У при Х = 0
    у = х³ - 5х = 0,
    Отсюда одно значение у = 0.
    С осью Х при У = 0
    Дробь равна 0, когда числитель равен 0
    х³ - 5х = 0,
    х(х² - 5) = 0
    х₁ = 0,
    х = +-√5,
    х₂ = -√5 = -2.2360679,
    х₃ = √5 = 2.2360679.
    4) Вычислить чётность/нечётность:
    f(-x) = ((-x)³ - 5(-x)) / (5 - 3(-x)) = -(x³ - 5x) / (5 - 3x²).
    То есть f(-x) = -f(x).
    Значит, функция нечётная.
    5) Выяснить периодичность - нет периодичности.
    6) Найти производную, промежутки монотонности функции, экстремумы:
    Производная\: частного: $$ ( \frac{f}{g})’ = \frac{f’g-g’f}{g^2} \\ \frac{d}{dx} (x^3-5x)=3x^2-5 \\ \frac{d}{dx} (5-3x^2)=-6x. $$
    После подстановки получаем $$ y’= \frac{-3x^4-25}{(5-3x^2)^2} $$
    Знаменатель производной в квадрате всегда положителен.
    В числителе переменная в чётной степени, а выражения с минусом.
    Значит, на каждом промежутке функции она убывающая.
    Производная не может быть равна 0 (из за наличия переменной в знаменателе), поэтому у функции нет ни максимума, ни минимума.
    7) Найти промежутки выпуклости, вогнутости, вторую производную и точки перегиба:
    для этого надо найти вторую производную:
    – если вторая производная меньше 0 на интервале, то график функции  является выпуклым на данном интервале;– если вторая производная больше 0 на интервале, то график функции  является вогнутым на данном интервале.
    Вторая производная равна:
    $$ f’’= \frac{60x(x^2+5)}{(3x^2-5)^3}. $$
    Нулю может быть равна только при х = 0.
    Это одна точка перегиба.
    В точках разрыва функция меняет выпуклость на вогнутость, но это не считается точкой перегиба, так как функция в этих точках не определена.
    8) Асимптоты графика функции (y=kx+b)
    Есть 2 вертикальные асимптоты в точках разрыва х₁ = -√(5/3)  и х₂ = √(5/3).
    уравнение наклонной асимптоты слева:  y = -х / 3,
    справа уравнение наклонной асимптоты такое же: y = -х / 3.
    9) Построить график. Смотри приложение.

    Найти ООФ  Если есть точки разрыва исследовать ихЭти вопроса практически совпадают так как ООФ включает точки разрыва Если переменная в знаменателе то есть точки разрыва при...

  • Исследовать функцию на экстремум:
    y=x^4-5x^2+4
    Общая схема построения графика функции:
    1) найти D(y)
    2) четная/нечетная/периодическая функция
    3) точки пересечения графика с осями координат
    4) найти асимптоты
    5) найти промежутки монотонности функции и ее экстремумы
    6) найти промежутки выпуклости графика функции точки перегиба
    7) построить график


    Решение: Y=x^4-5x^2+41)
    от -бесконечности до +бесконечности
    2)f(-x)=(-x)^4-5(-x)^2+4; f(-x)=f(x) - чётная
    3) на графике видно
    4)x - любое число, значит вертикальных асимптот нет. 
    5) монотонность - y’=4x^3-10x; 4x^3-10x=0; x=0 и x=sqrt(2,5);   x=sqrt(2,5)-экстремум y’(2,5)=0
    6) на промежутке (-беск;-sqrt(2,5)) - выпукла вниз, на (-sqrt(2,5);(sqrt(2,5) -в верх и (sqrt(2,5);+беск); - вниз.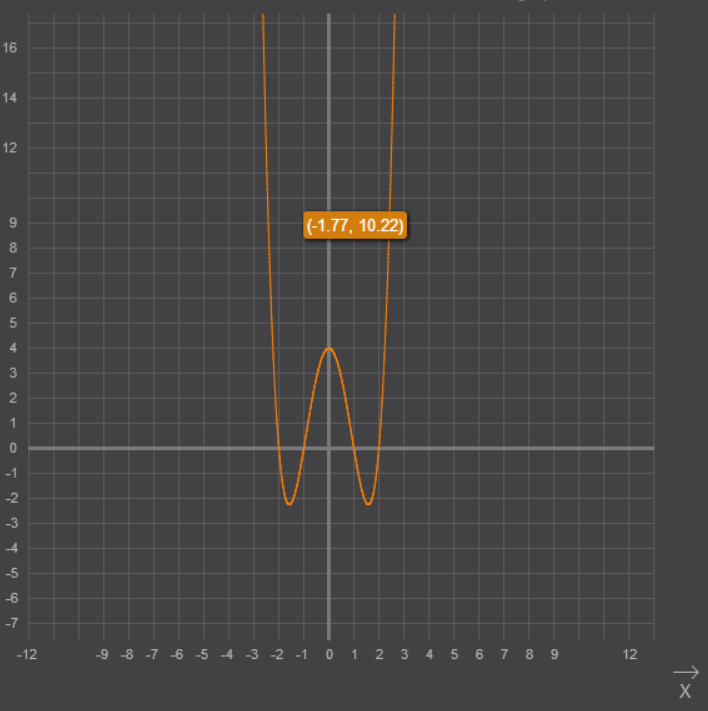

    Y x - x от -бесконечности до бесконечности f -x -x - -x f -x f x - ч тная на графике видно x - любое число значит вертикальных асимптот нет.  монотонность - y x - x x - x x и...

  • \( f(x)=2x+\frac{8}{x} \) Найти чётность, переодичность, точки пересечения с осями координат, Монотонность, ограниченность, экстремумы и их точки, промежутки знака постоянства. Уже 2 час немогу сделать
    PS \( f `(x)=2-\frac{8}{x^{2}} \)


    Решение: 1. Функция нечетная, непериодическая, точки пересечения с осью ординат не имеет (ось ординат является вертикальной асимптотой), с осью абсцисс пересекается в точке (2;0).

    2. Производная равна нулю при х = 2 и х = -2, на промежутке от минус бесконечности до - 2 положительна (функция монотонно возрастает), на промежутке от - 2 до 0 отрицательна (функция монотонно убывает), на промежутке от 0 до 2 отрицательна (функция монотонно убывает) и от 2 до плюс бесконечности положительна (функция монотонно возрастает).

    3. Точка х = -2 является первым экстремумом (точка максимума), точка х = 2 - вторым экстремумом (точка минимума). Точка х = 0 является точкой разрыва второго рода (бесконечного).

    4. Функция ограничена по вертикали прямой х = 0.

<< < 234 5 6 > >>