график функции »
область определения функции - страница 14
Обьясните на примере: y = 2x⁴-9x²+7
Можно показать на любом своём примере, только дробные не берите.
План анализа функции по пунктам:
1.) Найти область определения
2.) Определить четность\нечетность
3.) Выяснить наличие асимптот
4.) Найти точки пересечения графика с осями координат
5.) Найти производные
6.) Исследовать на монотонность и экстремум
, хотя бы немного, для меня это очень важно, завтра контрольная работа. 2, 5, 6 пункты решать НЕ НАДО
Решение: 1.) Найти область определенияобласть определения это все "х" при котором уравнеие функции имееер решение.
например y=$$ \sqrt{x} $$ область определения будет все х> или=0 (т. к. корень из отрицательного числа нельзя вывести)
или например у=$$ log_x2 $$ здесь обл. опр. х>0 и не равен нулю.
в твоем примере х Любой.
3) Выяснить наличие асимптот
асимптота- прямая к которой стремится график функции но никогда с ним не прикоснется. в твоем примере асимптоы нет. а например tgx имеет асимптоты в при тех х в которых tg не существует (-90, 90, 270.)
4) Найти точки пересечения графика с осями координат
здесь все просто: сначала приравниваем у к 0 и находим х. (это будут точки пересечения с осью х) на твоем примере $$ 0 = 2x^4-9x^2+7 $$ x=+1;-1;$$ +\sqrt{3.5} $$; $$ -\sqrt{3.5} $$ значит точки (1;0) (-1;0) ($$ \sqrt{3.5} $$;0) ($$ -\sqrt{3.5} $$;0)
затем аналогично берем х за 0 и находим у. (это пересечение с осью у) точка(0;7)
вот и все!
Дифференциальное исчисление-Полное исследование функции
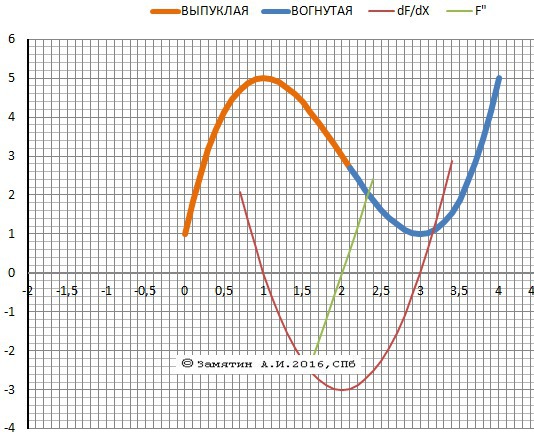
y=x^3-6x^2+9x+1,[0;4]
1. Найти область определения функции.
2. Установить чётность (нечётность) и периодичность функции.
3. Исследовать поведение функции на границах области определения и найти асимптоты графика функции.
4. Найти интервалы монотонности и экстремумы функции.
5. Найти интервалы направления выпуклости и точки перегиба графика функции.
6. Найти точки пересечения с осями координат и дополнительные точки; построить график функции.
Решение: ДАНО
х³-6х²+9х+1 на интервале Х∈[0,4].
ИССЛЕДОВАНИЕ
1. Область определения - R - все действительные.
разрывов нет - непрерывная.
2, Пересечение с осью Х - на интервале - нет.
3. На четность.
Y(-x) ≠ Y(+x) - функция ни четная ни нечетная.
4. Первая производная - экстремумы.
Y’ = 3x²-12x+9 = 3*(x-1)(x-3)0
5. Монотонность.
Возрастает - Х∈(-∞,1]∪[3,+∞)
Убывает - Х∈[1,3]
6. Экстремумы
Ymax(1) = 5
Ymin(3) = 1
7. Вторая производная.
Y" = 6x-12 = 6(x-2)
8. Точка перегиба
Y"(2) =0
9.
Выпуклая - Х∈(-∞,2]
Вогнутая - X∈[2,+∞).
10. Значения на границах отрезка.
Y(0) =1
Y(4) = 5
F(x)=(х+3)(х+1) Иследовать график функции по алгаритму_
1 Область определения
2. Исследование функции на четность, нечетность и периодичность
3. Нахождение точек пересечения графика функции с осями координат
Точки пересечения с осью ОХ:, где – решение уравнения.
Точки пересечения с осью ОY:.
4. Нахождение промежутков знакопостоянства функции
5. Нахождение производной функции, области определения производной, критических точек
6. Нахождение промежутков возрастания, убывания, точек экстремума и экстремумов
Критические точки функции разбивают область определения функции на промежутки. Для нахождения промежутков возрастания, убывания и точек экстремума нужно определить знак производной на каждом из полученных промежутков. Если производная функции положительна на некотором промежутке I, то функция возрастает на этом промежутке; если производная функции отрицательна на некотором промежутке I, то функция убывает на этом промежутке. Если при переходе через критическую точку производная меняет знак, то данная точка является точкой экстремума.
7. Нахождение промежутков выпуклости функции и точек перегиба
Для нахождения промежутков выпуклости используется вторая производная функции. Точки, в которых вторая производная равна нулю или не существует, разбивают область определения функции на промежутки. Если вторая производная на полученном промежутке положительна, то график функции имеет выпуклость вниз, если – отрицательна, то график функции имеет выпуклость вверх. Если при переходе через точку, в которой вторая производная равна нулю или не существует, вторая производная меняет знак, то данная точка является точкой перегиба.
8. Исследование поведения функции на бесконечности и в окрестности точек разрыва
Для исследования поведения функции в окрестности точки разрыва необходимо вычислить односторонние пределы: и. Если хотя бы один из данных пределов равен бесконечности, то говорят, что прямая – вертикальная асимптота.
При исследовании поведения функции на бесконечности необходимо проверить, не имеет ли график функции наклонных асимптот при и. Для этого нужно вычислить следующие пределы: и. Если оба предела существуют, то – уравнение наклонной асимптоты при. Частный случай наклонной асимптоты при – горизонтальная асимптота. Аналогично ищется наклонная асимптота при.
9. Построение графика (при необходимости нужно найти значения функции в дополнительных точках)
Решение: Функцию (х+3)(х+1) проще исследовать после преобразования:
(х+3)(х+1) = х²+3х+х+3 = х²+4х+3 - это уравнение параболы.
Результаты исследования графика функцииОбласть определения функции. ОДЗ: -00<x<+00
Точка пересечения графика функции с осью координат Y: График пересекает ось Y, когда x равняется 0: подставляем x=0 в x^2+4*x+3.
Результат: y=3. Точка: (0, 3)
Точки пересечения графика функции с осью координат X: График функции пересекает ось X при y=0, значит нам надо решить уравнение:x^2+4*x+3 = 0 Решаем это уравнение и его корни будут точками пересечения с X:
x=-3.0. Точка: (-3.0, 0) x=-1.0. Точка: (-1.0, 0)
Экстремумы функции: Для того, чтобы найти экстремумы, нужно решить уравнение y’=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:y’=2*x + 4=0 (Производную находим, a уравнение решаем )
Решаем это уравнение и его корни будут экстремумами:x=-2.0. Точка: (-2.0,1.0)
Интервалы возрастания и убывания функции: Найдем интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим на ведет себя функция в экстремумах при малейшем отклонении от экстремума: Минимумы функции в точках:-2.0 Максимумов у функции нету
Возрастает на промежутках: [-2.0, oo) Убывает на промежутках: (-oo,2.0]
Точки перегибов графика функции: Найдем точки перегибов для функции, для этого надо решить уравнение y’’=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции,
+ нужно подсчитать пределы y’’ при аргументе, стремящемся к точкам неопределенности функции:y’’=2=0 - нет перегибов.
Вертикальные асимптоты Нету Горизонтальные асимптоты графика функции: Горизонтальную асимптоту найдем с помощью предела данной функции при x->+oo и x->-oo. Соотвествующие пределы находим :lim x^2+4*x+3, x->+oo = oo, значит горизонтальной асимптоты справа не существует lim x^2+4*x+3, x->-oo = oo, значит горизонтальной асимптоты слева не существует Наклонные асимптоты графика функции: Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при x->+oo и x->-oo. Находим пределы :lim x^2+4*x+3/x, x->+oo = oo, значит наклонной асимптоты справа не существуетlim x^2+4*x+3/x, x->-oo = -oo, значит наклонной асимптоты слева не существует
Четность и нечетность функции: Проверим функцию четна или нечетна с помощью соотношений f(x)=f(-x) и f(x)=-f(x). Итак, проверяем:x^2+4*x+3 = x^2 - 4*x + 3 - Нет x^2+4*x+3 = -(x^2 - 4*x + 3) - Нет - значит, функция не является ни четной ни нечетнойПостроить график функции y = 2*∛(x²) * e^(-x/3) по следующему алгоритму:
1) Область определения функции
2) Непрерывность функции и её четность(lim y =? при x-> +- ∞)
3) Пересечение с осями координат и точки разрыва (найти точки разрыва с помощью пределов)
4) Асимптоты (вертикальные и наклонные, найти их через пределы)
5) Возрастание, убывание, экстремумы функции(через достаточные условия)
6) Выпуклость, вогнутость и перегибы графика
7) Построить сам график со всеми асимптотами
Решение: Дано:
$$ y = \sqrt[3]{x^2} e^{ -\frac{x}{3} } $$ ;
Исследовать функцию и построить график.
Решение:
1) Функция определена при любых аргументах.
D(f) ≡ R ≡ $$ ( -\infty ; +\infty ) $$ ;
2) Функция не является ни чётной, ни нечётной. Докажем это:
$$ y(-x) = \sqrt[3]{ (-x)^2 } e^{ -\frac{-x}{3} } = \sqrt[3]{ x^2 } e^{ \frac{x}{3} } $$ ;
$$ y(-x)/y(x) = \frac{ \sqrt[3]{ x^2 } \exp{ \frac{x}{3} } }{ \sqrt[3]{ x^2 } \exp{ ( -\frac{x}{3} ) } } = \frac{ \exp{ \frac{x}{3} } }{ \exp{ -\frac{x}{3} } } = \exp{ \frac{x}{3} } \exp{ \frac{x}{3} } = \exp{ \frac{2x}{3} } $$ ≠ ± 1 при любых аргументах ;
$$ y(-x)/y(x) $$ ≠ ± 1 ;
Найдём первую производную функции y(x) :
$$ y’(x) = ( \sqrt[3]{x^2} e^{ -\frac{x}{3} } )’ = ( x^\frac{2}{3} e^{ -\frac{x}{3} } )’ = \frac{2}{3} x^{ -\frac{1}{3} } e^{ -\frac{x}{3} } + x^\frac{2}{3} ( -\frac{1}{3} ) e^{ -\frac{x}{3} } = \\ = \frac{ e^{ -\frac{x}{3} } }{3} ( \frac{2}{x^\frac{1}{3} } - x^\frac{2}{3} ) = \frac{ e^{ -\frac{x}{3} } }{ 3 x^{1/3} } ( 2 - x ) $$ ;
$$ y’(x) = \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( 2 - x ) $$ ;
При x = 0, производная y’(x) – не определена, хотя сама функция определена при любых аргументах, так что функция непрерывна на всей числовой прямой, но непрерывно-дифференцируема за исключением ноля.
Убедимся в этом, вычислив предел около ноля слева и справа
$$ \lim_{x \to -0} y(x) = \lim_{x \to -0} \sqrt[3]{x^2} e^{ \frac{x}{3} } = \sqrt[3]{ (-0)^2 } e^{ -\frac{-0}{3} } = \sqrt[3]{0} e^{0} = 0*1 = 0 $$ ;
$$ \lim_{x \to +0} y(x) = \lim_{x \to +0} \sqrt[3]{x^2} e^{ \frac{x}{3} } = \sqrt[3]{ (+0)^2 } e^{ -\frac{0}{3} } = \sqrt[3]{0} e^{0} = 0*1 = 0 $$ ;
3) Функция определена при любых x, поэтому точек разрыва нет.
Если приравнять функцию к нолю, получим:
$$ y(x) = 0 $$ ;
$$ \sqrt[3]{x^2} e^{ \frac{x}{3} } = 0 $$ ;
Что возможно только при $$ \sqrt[3]{x^2} = 0 $$, т. е. при x = 0 ;
Итак, точка ( 0 ; 0 ) – принадлежит нашему графику.
4. Найдем асимптоты y(x).
Точек разрыва нет, значит, нет и вертикальных асимптот.
Посмотрим, что происходит с функцией y(x) при устремлении аргумента к ± $$ \infty $$ :
$$ \lim_{x \to -\infty} y(x) = \lim_{x \to -\infty} \sqrt[3]{x^2} e^{ -\frac{x}{3} } = \lim_{x \to -\infty} e^{ \ln{ \sqrt[3]{x^2} } } e^{ -\frac{x}{3} } = \\ = \lim_{x \to -\infty} e^{ \frac{2}{3} \ln{ (-x) } } e^{ \frac{-x}{3} } = \lim_{x \to -\infty} e^{ \frac{2}{3} \ln{ (-x) } + \frac{-x}{3} } = \\ = \lim_{x \to -\infty} e^{ \frac{-x}{3} ( 1 + \frac{ 2 \ln{ (-x) } }{ -x } ) } > \lim_{x \to -\infty} e^{ \frac{-x}{3} } = +\infty $$ ;
$$ \lim_{x \to -\infty} y(x) = +\infty $$ ;
$$ \lim_{x \to +\infty} y(x) = \lim_{x \to +\infty} \sqrt[3]{x^2} e^{ -\frac{x}{3} } = \lim_{x \to +\infty} e^{ \ln{ \sqrt[3]{x^2} } } e^{ -\frac{x}{3} } = \\ = \lim_{x \to +\infty} e^{ \frac{2}{3} \ln{x} } e^{ -\frac{x}{3} } = \lim_{x \to +\infty} e^{ \frac{2}{3} \ln{x} - \frac{x}{3} } = \\ = \lim_{x \to +\infty} e^{ -\frac{x}{3} ( 1 - \frac{ 2 \ln{x} }{x} ) } < \lim_{x \to +\infty} e^{ -\frac{x}{3} } \leq 0 $$ ;
Поскольку, $$ \lim_{x \to +\infty} y(x) \geq 0 $$, то:
$$ \lim_{x \to +\infty} y(x) = 0 $$ ;
Значит, уходя на отрицательную ∞ аргумента y(x) и сама стремиться к бесконечности, а уходя на положительную бесконечно по аргументу y(x) стремится к нулю ;
Из этого следует, что при x>0 есть горизонтальная асимптота y = 0.
Чтобы найти наклонную асимптоту, найдем предел первой производной на отрицательной бесконечности по аргументу:
$$ \lim_{x \to -\infty} y’(x) = \lim_{x \to -\infty} \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( 2 - x ) > \lim_{x \to -\infty} \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( - x ) $$ ;
$$ \lim_{x \to -\infty} \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( - x ) = \lim_{x \to -\infty} ( -\frac{1}{3} \sqrt[3]{x^2} e^{ -\frac{x}{3} } ) = -\infty $$ – по доказанному в пределе самой функции.
$$ \lim_{x \to -\infty} y’(x) = -\infty $$ ;
А это означает, что наклонной асимптоты на отрицательной бесконечности нет. А на положительной – горизонтальная.
Построить график функции y = 2∛(x²) * e^(x/3) по следующему алгоритму:
1) Область определения функции
2) Непрерывность функции и её четность(lim y =? при x-> +- ∞)
3) Пересечение с осями координат и точки разрыва (найти точки разрыва с помощью пределов)
4) Асимптоты (вертикальные и наклонные, найти их через пределы)
5) Возрастание, убывание, экстремумы функции(через достаточные условия)
6) Выпуклость, вогнутость и перегибы графика
7) Построить сам график со всеми асимптотами
Решение: Дано:
$$ y = \sqrt[3]{x^2} e^{ -\frac{x}{3} } $$ ;
Исследовать функцию и построить график.
Решение:
1) Функция определена при любых аргументах.
D(f) ≡ R ≡ $$ ( -\infty ; +\infty ) $$ ;
2) Функция не является ни чётной, ни нечётной. Докажем это:
$$ y(-x) = \sqrt[3]{ (-x)^2 } e^{ -\frac{-x}{3} } = \sqrt[3]{ x^2 } e^{ \frac{x}{3} } $$ ;
$$ y(-x)/y(x) = \frac{ \sqrt[3]{ x^2 } \exp{ \frac{x}{3} } }{ \sqrt[3]{ x^2 } \exp{ ( -\frac{x}{3} ) } } = \frac{ \exp{ \frac{x}{3} } }{ \exp{ -\frac{x}{3} } } = \exp{ \frac{x}{3} } \exp{ \frac{x}{3} } = \exp{ \frac{2x}{3} } $$ ≠ ± 1 при любых аргументах ;
$$ y(-x)/y(x) $$ ≠ ± 1 ;
Найдём первую производную функции y(x) :
$$ y’(x) = ( \sqrt[3]{x^2} e^{ -\frac{x}{3} } )’ = ( x^\frac{2}{3} e^{ -\frac{x}{3} } )’ = \frac{2}{3} x^{ -\frac{1}{3} } e^{ -\frac{x}{3} } + x^\frac{2}{3} ( -\frac{1}{3} ) e^{ -\frac{x}{3} } = \\ = \frac{ e^{ -\frac{x}{3} } }{3} ( \frac{2}{x^\frac{1}{3} } - x^\frac{2}{3} ) = \frac{ e^{ -\frac{x}{3} } }{ 3 x^{1/3} } ( 2 - x ) $$ ;
$$ y’(x) = \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( 2 - x ) $$ ;
При x = 0, производная y’(x) – не определена, хотя сама функция определена при любых аргументах, так что функция непрерывна на всей числовой прямой, но непрерывно-дифференцируема за исключением ноля.
Убедимся в этом, вычислив предел около ноля слева и справа
$$ \lim_{x \to -0} y(x) = \lim_{x \to -0} \sqrt[3]{x^2} e^{ \frac{x}{3} } = \sqrt[3]{ (-0)^2 } e^{ -\frac{-0}{3} } = \sqrt[3]{0} e^{0} = 0*1 = 0 $$ ;
$$ \lim_{x \to +0} y(x) = \lim_{x \to +0} \sqrt[3]{x^2} e^{ \frac{x}{3} } = \sqrt[3]{ (+0)^2 } e^{ -\frac{0}{3} } = \sqrt[3]{0} e^{0} = 0*1 = 0 $$ ;
3) Функция определена при любых x, поэтому точек разрыва нет.
Если приравнять функцию к нолю, получим:
$$ y(x) = 0 $$ ;
$$ \sqrt[3]{x^2} e^{ -\frac{x}{3} } = 0 $$ ;
Что возможно только при $$ \sqrt[3]{x^2} = 0 $$, т. е. при x = 0 ;
Итак, точка ( 0 ; 0 ) – принадлежит нашему графику.
4. Найдем асимптоты y(x).
Точек разрыва нет, значит, нет и вертикальных асимптот.
Посмотрим, что происходит с функцией y(x) при устремлении аргумента к ± $$ \infty $$ :
$$ \lim_{x \to -\infty} y(x) = \lim_{x \to -\infty} \sqrt[3]{x^2} e^{ -\frac{x}{3} } = \lim_{x \to -\infty} e^{ \ln{ \sqrt[3]{x^2} } } e^{ -\frac{x}{3} } = \\ = \lim_{x \to -\infty} e^{ \frac{2}{3} \ln{ (-x) } } e^{ \frac{-x}{3} } = \lim_{x \to -\infty} e^{ \frac{2}{3} \ln{ (-x) } + \frac{-x}{3} } = \\ = \lim_{x \to -\infty} e^{ \frac{-x}{3} ( 1 + \frac{ 2 \ln{ (-x) } }{ -x } ) } > \lim_{x \to -\infty} e^{ \frac{-x}{3} } = +\infty $$ ;
$$ \lim_{x \to -\infty} y(x) = +\infty $$ ;
$$ \lim_{x \to +\infty} y(x) = \lim_{x \to +\infty} \sqrt[3]{x^2} e^{ -\frac{x}{3} } = \lim_{x \to +\infty} e^{ \ln{ \sqrt[3]{x^2} } } e^{ -\frac{x}{3} } = \\ = \lim_{x \to +\infty} e^{ \frac{2}{3} \ln{x} } e^{ -\frac{x}{3} } = \lim_{x \to +\infty} e^{ \frac{2}{3} \ln{x} - \frac{x}{3} } = \\ = \lim_{x \to +\infty} e^{ -\frac{x}{3} ( 1 - \frac{ 2 \ln{x} }{x} ) } < \lim_{x \to +\infty} e^{ -\frac{x}{3} } \leq 0 $$ ;
Поскольку, $$ \lim_{x \to +\infty} y(x) \geq 0 $$, то:
$$ \lim_{x \to +\infty} y(x) = 0 $$ ;
Значит, уходя на отрицательную ∞ аргумента y(x) и сама стремиться к бесконечности, а уходя на положительную бесконечно по аргументу y(x) стремится к нулю ;
Из этого следует, что при x>0 есть горизонтальная асимптота y = 0.
Чтобы найти наклонную асимптоту, найдем предел первой производной на отрицательной бесконечности по аргументу:
$$ \lim_{x \to -\infty} y’(x) = \lim_{x \to -\infty} \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( 2 - x ) < \lim_{x \to -\infty} \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( - x ) $$ ;
$$ \lim_{x \to -\infty} \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( - x ) = \lim_{x \to -\infty} ( -\frac{1}{3} \sqrt[3]{x^2} e^{ -\frac{x}{3} } ) = -\infty $$ – по доказанному в пределе самой функции.
$$ \lim_{x \to -\infty} y’(x) = -\infty $$ ;
А это означает, что наклонной асимптоты на отрицательной бесконечности нет. А на положительной – горизонтальная.
Кроме того, легко показать, что:
$$ \lim_{x \to -0} y’(x) = -\infty $$,
а $$ \lim_{x \to +0} y’(x) = +\infty $$, поскольку:
$$ \lim_{x \to -0} y’(x) = \lim_{x \to -0} \frac{ e^{ -\frac{-0}{3} } }{ 3 \sqrt[3]{-0} } ( 2 - (-0) ) = -\infty $$ и:
$$ \lim_{x \to +0} y’(x) = \lim_{x \to +0} \frac{ e^{ -\frac{+0}{3} } }{ 3 \sqrt[3]{+0} } ( 2 - (+0) ) = +\infty $$ ;
А всё это значит, что график входит в критическую точку ( 0, 0 ) сверху вниз вдоль оси Oy и выходит вдоль неё же снизу вверх.
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...