график функции »

область определения функции - страница 12

  • 8. Докажите что значение выражения является рациональным числом✓(6-✓11)*✓(6+✓11) 9. при каком значении уравнение имеет единственный корень 2x^2-4x+t=0 10. Найдите область определения выражения ✓(7-14х)/х+8


    Решение: (6-V11)*(6+V11) = 6^2 - V11^2 = 36 - 11 = 25 

    (25 = 5^2)

    2X^2 - 4X + T = 0

    D = 0

    D = 16 - 4*2*T = 0

    8T = 16

    T = 2

    7 - 14X > 0 -> X > 2

    7 - 14X < 0 -> X < 2

    X + 3 не равен нулю -> X не равен - 3

  • В каком случае считают, что область определения функции состоит из всех значений независимой переменной?
    Сформулируйте определение линейной функции.
    Какую функцию называют линейной?
    Как найти координаты точки пересечения?


    Решение: Вспомним, что Д(у) есть множество всех значений х, при которых все указанные действия могут выполняться
    Тогда все значения она может принимать, если нет деления или извлечения квадратного корня(корня четной степени).
    Линейная функция - функция вида y=kx+b, где k, b-числа.
    Точка пересечения с осью Х находим, приравнивая выражение к нулю(y=0),
    а с осью Y берем х=0.

    Область определения функции состоит из всех значений независимой переменной x, когда в уравнении функции отсутствуют выражения, которые могут не иметь смысла
    Линейная функция это функция имеющая вид y=kx+b, где k и b числа, а x переменная
    Для её построения нужно знать координаты двух точек (это прямая)
    Чтобы найти координаты точки пересечения графика с осью абсцисс нужно подставить под y число 0, так как в таких точках ордината равна 0
    . с осью ординат - под x подставляем 0, так как в таких точках абсцисса равна 0

  • Выполните исследование функции по следующей схеме:
    1) Найти область определения
    2) проверить четность, нечетность функции
    3) найти точки пересечения с осями координат
    4) найти экстремумы функции и интервалы монотонности
    5) найти точки перегиба и интервалы выпуклости и вогнутости
    6) построить график функции
    y=2x^4-4x^2+3
    Пожалуйстааааа


    Решение: Y=2x⁴-4x²+3
    1) x∈R
    2) y(-x)=2(-x)⁴-4x²+3=y(x) ф-я четная, можно строить только при х больше 0 и отразить график симметрично в оси у
    3) пересечение с осью х у=0
    2x⁴-4x²+3=0 сделаем замену x²=z
    2z²-4z+3=0 D=16-24<0 корней нет, график лежит
    выше оси х, х=0 у=3 пересечение с осью у
    4)y’=8x³-8x=8x(x-1)(x+1) экстремумы при x=0,1,1
    -1- 0 -1-→x
      - + - +
    убывает при x∈(-∞;-1)∪(0;1)
    возрастает x∈(1;0)∪(1;∞) x= -1,1 min y= 1
    x=0 max y=3.
    5) y’’= 24x²-8=8(3x²-1)=0 x=1/√3,1/√3 точки перегиба
    - 1/√3-1/√3-
      + - +
    вогнута выпукла вогнута
    -

  • Исследуйте функцию и постройте график
    1) Найти область определения функции.
    2) Выяснить, не является ли функция чётной, нечётной или периодической.
    3) Найти точки пересечения графика с осями координат.
    4) Найти асимптоты графика функции.
    5) Найти промежутки монотонности функции и её экстремумы.
    6) Найти промежутки выпуклости графика функции и точки перегиба.
    7) Построить график, используя полученные результаты исследования.
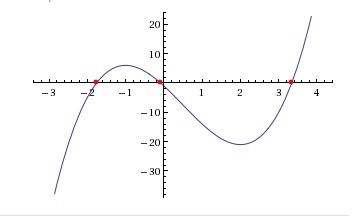
    \( y=2x^3-3x^2-12x-1 \)


    Решение: Обычная кубическая парабола
    1) Область определения - (-оо; +оо)
    2) Ни четная, ни нечетная, не периодическая.
    3) y(0) = -1; y = 0 в трех иррациональных точках
    x1 ~ -1,755; x2 ~ -0,085; x3 ~ 3,34
    4) Асимптот нет
    5) y ’ = 6x^2 - 6x - 12 = 6(x^2 - x - 2) = 6(x - 2)(x + 1) = 0
    x1 = -1; y(-1) = -2 - 3 + 12 - 1 = 6 - максимум
    x2 = 2; y(2) = 2*8 - 3*4 - 12*2 - 1 = 16 - 12 - 24 - 1 = -21 - минимум
    При x = (-oo; -1) U (2; +oo) - возрастает
    При x = (-1; 2) - убывает
    6) y ’’ = 12x - 6 = 6(2x - 1) = 0
    x = 1/2; y(1/2) = 2/8 - 3/4 - 12/2 - 1 = -1/2 - 6 - 1 = - 7,5 - точка перегиба
    При x < 1/2 будет y ’’ < 0; график выпуклый вверх.
    При x > 1/2 будет y ’’ > 0, график выпуклый вниз.
    7) График

    Обычная кубическая парабола Область определения - -оо оо Ни четная ни нечетная не периодическая. y - y в трех иррациональных точкахx - x - x Асимптот нет y x - x - x - x - x...

  • \( y = 2 x^{2} + \frac{4}{x} \)
    1) Найти область определения функции
    2) Найти точки пересечения координат
    3) Найти промежутки возрастания и убывания
    4) Найти точки экстремума
    5) Построить график


    Решение: $$ y=2x^2+ \frac{4}{x}. $$
    1) Найти область определения функции: x ≠ 0.
    2) Найти точки пересечения координат: так как х находится в знаменателе дроби, то пересечения с осью у нет.
    Для определения пересечения с осью х надо решить уравнение 2х²+(4/х) = 0.
    Приведём к общему знаменателю: (2х³+4)/х = 0.
    Дробь равна 0, когда числитель равен 0:
    2х³+4=0,
    х³=-4/2 = -2,
    х =∛(-2) =  -1.25992.
    3) Найти промежутки возрастания и убывания:
    Находим производную: y’ = 4x-(4/x²) и приравниваем её 0:
    4x-(4/x²) = 0.
    Приведём к общему знаменателю: (4х³-4)/х² = 0.
    Дробь равна 0, когда числитель равен 0:
    4х³-4 = 0,
    х³ = 4/4 = 1,
    х= ∛1 = 1.
    Если производная отрицательна, то функция убывает, если производная положительна, то функция возрастает.
    Находим значения производной вблизи критической точки:
    х  -2 -1  0 0.5 1  2
    y ’  -9  -8 -14 0  7.
    Отсюда видно:
    Функция возрастает x > 1 или х ∈ (1;∞),
      убывает х < 0; 0 <x < 1 или х ∈ (-∞;0) ∪ (0;1].  
    4) Найти точки экстремума:
    Она уже найдена - это локальный минимум в точке х = 1.
    Вблизи этой точки производная функции меняет знак с минуса на плюс.
    5) Построить график - он дан .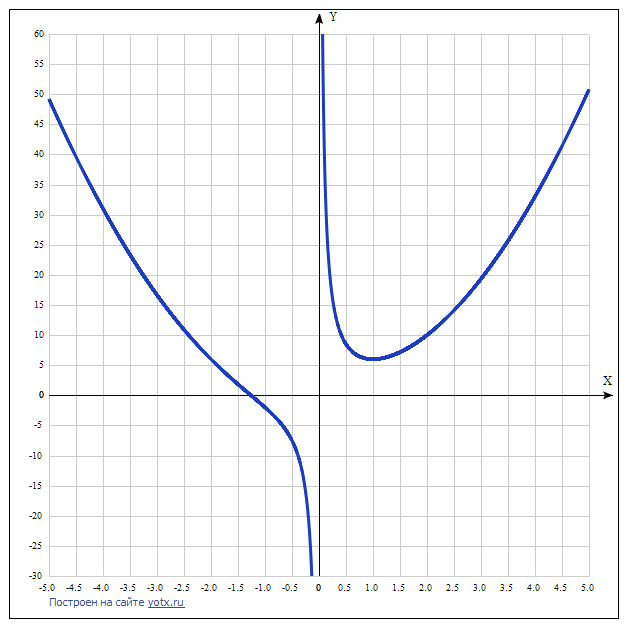

    y x frac x . Найти область определения функции x  . Найти точки пересечения координат так как х находится в знаменателе дроби то пересечения с осью у нет.Для определения пере...
<< < 101112 13 14 > >>