область определения функции - страница 11

2) Упростите выражение: cos^2 L - Cos^4 L+sin^4 L

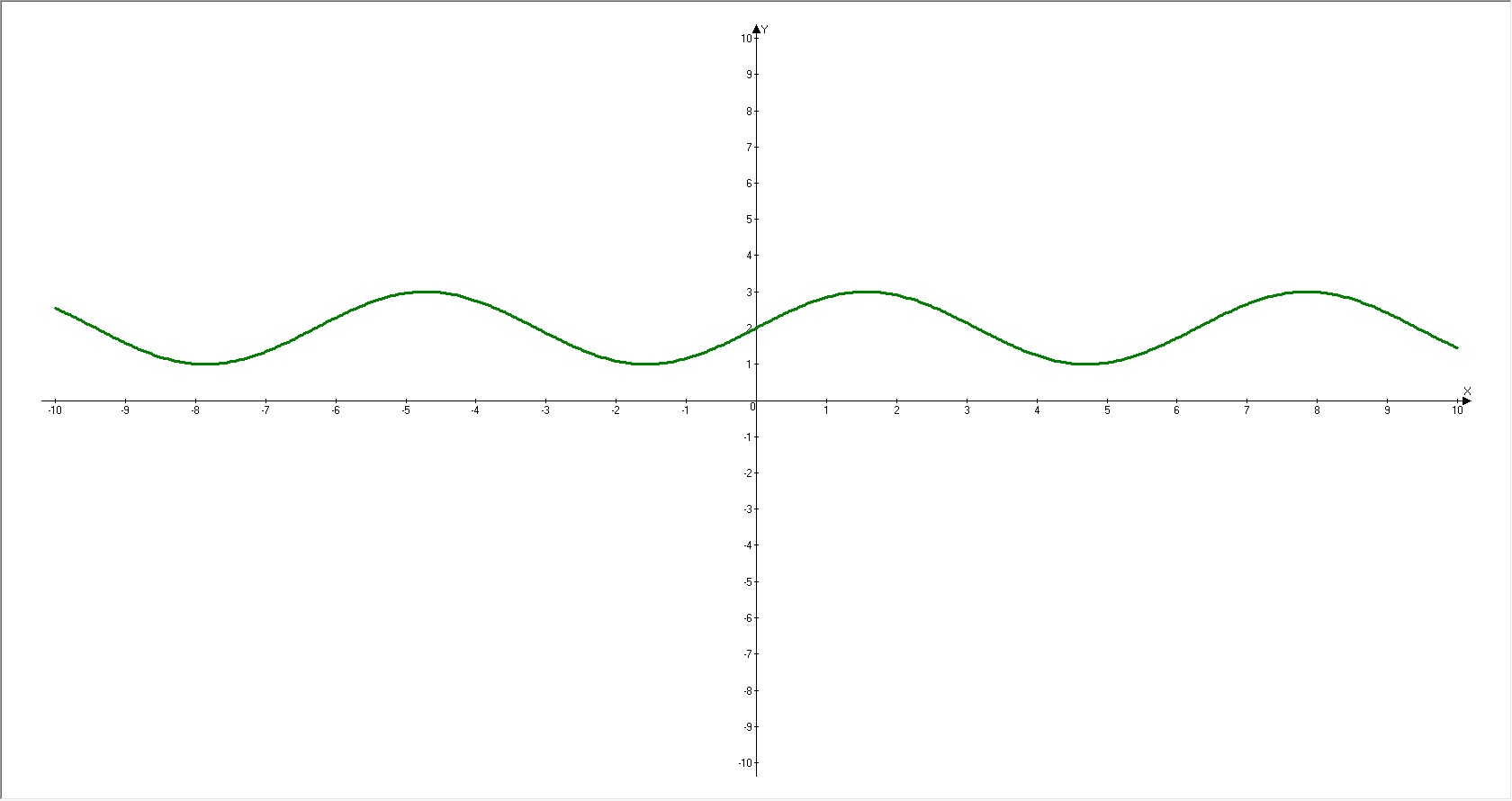
3. Найдите область определения и область значения функции y=2+sin x. постройте график функции

4. решите сис-му уравнений

1 уравнение: 3x+5y=-4

2 уравнение: -x+3y=6

6. Найдите производные функции: а)y=0,5 - 6х б)y=(1/(3x^2))-((x^3)/3)+2/x в) y=(2+x)/x

7) найдите интегралы

интеграл(3x-2)dx б) интеграл (6/(1+x^2))dx в) интеграл в верху 1 внизу -2 (3x^2 -15)dx

8) Из точки А отстоящей от плоскости на 12 см, проведена к этой плоскости наклонная АВ равная 37 см. Найти проэкцию АВ на данную плоскость (предварительно выполнив рисунок)

9) Как изменится полная поверхность куба, если его ребро увеличить в 3 раза

Решение: $$ 2) cos^2 L - cos^4 L+sin^4 L= cos^2 L -( cos^4 L-sin^4 L)=\\=cos^2L-(cos^2L-sin^2L)=sin^2L $$

3)D(x)=R;E(y)=[1;3], график во вложении 1.

4)$$ \begin{cases} 3x+5y=-4\\-x+3y=6|*3 \end{cases}\ \begin{cases} 3x+5y=-4\\+\\-3x+9y=18 \end{cases}\\14y=14\\y=1\\3x+5=-4\\3x=-9\\x=-3 $$

Ответ:(-3;1)

8)$$ AC=\sqrt{37^2-12^2}=\sqrt{25*49}=35 $$Вложение 2

9) Было a Площадь поверхности 6a^2

Стало 3a Площадь поверхности 9*6a^2

Ответ: увеличится в 9 раз
2. Найдите интеграл x^2dx/3+x^2.
3. вычислите 15^(-2)*45^5/3/75^4/3+2^1/4*4^3/8
4. Найдите область определения функции y=lg(1-x-2x^2).
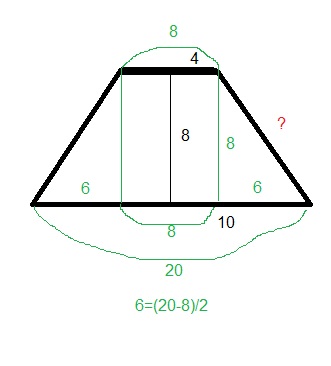
5. радиусы оснований усеченного конуса равны 10 см и 4 см а высота равна 8 см найдите образующую усеченного конуса.

Решение: $$ 2) \int\limits { \frac{ x^{2} }{3+ x^{2} } } \, dx = \int\limits { \frac{ x^{2} +3-3}{ 3+x^{2} } } \, dx = \int\limits {(1- \frac{3}{3+ x^{2} } } \, dx =x-3\cdot \frac{1}{ \sqrt{3} } arctg \frac{x}{ \sqrt{3} }+C $$
Ответ.$$ x-{\sqrt{3}\cdot arctg \frac{x}{ \sqrt{3} }+C \\ 3) \frac{15 ^{-2}\cdot45 ^{ \frac{5}{3} } }{75 ^{ \frac{4}{3} } } +2 ^{ \frac{1}{4} } \cdot4 ^{ \frac{3}{8} }= \frac{ \sqrt[3]{45 ^{5} } }{15 ^{2}\cdot \sqrt[3]{75 ^{4} } }}+2 ^{ \frac{1}{4} }\cdot (2 ^{2}) ^{ \frac{3}{8} } = \\ = \frac{45\cdot \sqrt[3]{45 ^{2} } }{225\cdot 75\cdot \sqrt[3]{75} }+2 ^{ \frac{1}{4}+ \frac{6}{8} } = \frac{3 \sqrt[3]{75} }{375 \sqrt[3]{75} }+2= \frac{1}{125}+2=2,008 $$
4) областью определения логарифмической функции является множество положительных чисел, значит выражение написанное под знаком логарифма должно быть больше 0:
1- х - 2х² > 0,
2x² + x -1 <0
Решаем квадратное уравнение: 2x² + x -1 =0, D=b²-4ac=1-4·2(-1)=9
x=(-1-3)/2=-2 или х= (-1+3)/2=1
Решением неравенства будет интервал (-2;1)
5) Сечение усеченного конуса, проходящее через высоту конуса и диаметры оснований - равнобедренная трапеция. С основаниями 2R=2·10=20 cм и 2r=2·4=8см. Высота трапеции H=8 см. По теореме Пифагора ( см. рисунок)
образующая L²=H²+((20-8)/2)²=8²+6²=100=10²
ответ. Образующая 10 см

$int limits frac x x dx int limits frac x - x dx int limits - frac x dx x- cdot frac sqrt arctg frac x sqrt C Ответ. x- sqrt cdot arctg frac x sqrt C frac - cdot frac frac fra...$
Исследовать функцию y=(5-х2)/(х2+5):1) найти область определения функции 2) исследовать функцию на непрерывность 3) определить, является ли данная функция четной, нечетной 4) найти интервалы возрастания и убывания функции и точки экстремума 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба 6) найти асимптоты графика функции. )

Решение: ДАНО
Y = (5-x²)/(5+x²)
Исследование.
1. Область определения.
Х∈(-∞;+∞)
2. Непрерывная. Точек разрыва нет.
3. Исследование на четность.
У(х) = У(-х) - функция четная.
4. Поиск экстремумов.
Первая производная
$$ Y’=- \frac{2x}{x^2+5}- \frac{2x(5-x^2)}{(x^2+5)^2} $$
Нули производной.
Y’ = 0 при х=0.
Максимум - Y(0) = 1.
Возрастает - Х∈(-∞;0]
Убывает - Х∈[0;+∞).
Минимум - Y(∞) = - 19/21.
5. Точки перегиба - нули второй производной.
$$ Y"= \frac{60x^2-100}{x^6+15x^4+75x^2+125} $$
Y"=60x²-100 = 0
x= √1.6 = +/- 1.26
6. Наклонная асимптота -
Y= -1.
На рисунке кроме графика функции дополнительно графики производных - точки экстремума и перегиба.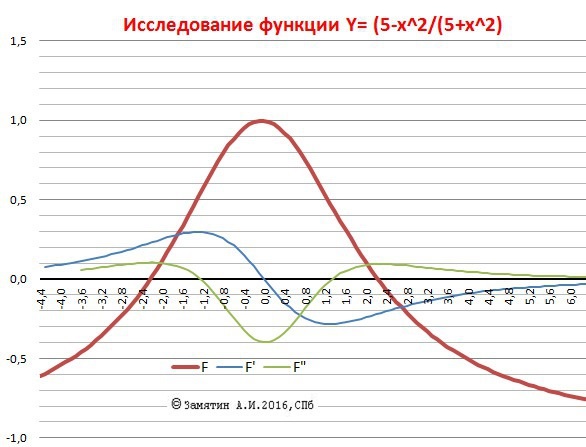
Исследовать функцию y= (2)/(1+x^2) по следующей схеме:
1) Найдите область определения функции
2) Исследовать функцию на непрерывность
3) Определить, является ли данная функция четной, нечетной.
4) найти интервалы возрастания и убывания функции и точки экстремума
5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба
6) найти асимптоты графика функции

Решение: ДАНО
Y = 2/(x²+1)
ИССЛЕДОВАНИЕ
1. Область определения. Х∈(-∞,+∞).
2. Пересечение с осью Х - нет. Х∈∅.
3. Пересечение с осью У. Х=0, У(0) = 2.
4. Поведение на бесконечности.
У(-∞) = 0, У(+∞) = 0.
5. Исследование на четность.
У(-х) = - У(х) - функция четная.
6. Поиск экстремумов по первой производной.
Y’ = -4x/(x²+1)² =
Нули производной при Х = +/- 1.
Минимум - Ymin(-1) = -1
Максимум - Ymax(1) = 1.
7. Возрастает - Х∈(-∞,0]
Убывает - X∞[0,+∞)
8. Точки перегиба по второй производной.
$$ Y"= \frac{12x^2-4}{x^6+3x^4+3x^2+1} $$
12x²-4 = 0
x = +/- √3/3 ~ 0.58
9. Асимптота. F(∞) = Y(x)/x = 0.
10. График прилагается.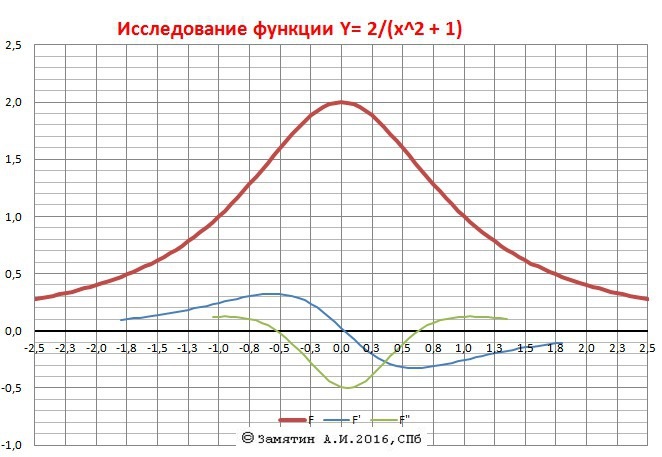
1) Найдите область определения функции, если:
g(x)=2x-1
2) Найдите нули функции, промежутки знакопостоянства и область значений функций, если:
f(x)=5x-1, где D(f)= [-2;2]
3) Представьте в стандартном виде число а= 0,00073 * 10^15 и найдите порядок числа:
а) а * 10^7
б) а * 0,001
в) а^2 * 0,000001
4) Представьте выражение в виде рациональной дроби:
a) $ ab^{-1} + a^{-1}b $
б) $ a^{-1}(a^{-1}+b^{-1} ) $

Решение: 1) область определения D(g) = ( - оо ; + оо )
2)    f(x) = 5x-1 где D(f)= [-2;2]
    Нули функции :
f(x) = 0
   5x-1 = 0
   5x = 1
   х = 1/5
   Промежутки знакопостоянства:
   f(x) > 0 при х ∈ ( 1/5 ; 2)
   f(x) < 0 при х ∈ ( -2 ; 1/5)
   Область значений функции :
   f(-2) = 5*(-2) -1 = -11
   f(2) = 5*2 -1 = 9
   E(f)= [-11;9]
3) а= 0,00073 * 10^15 = 7,3 * 10^11 порядок числа: 11
   а) а * 10^7 = 7,3 * 10^11 * 10^7 = 7,3 * 10^18
   б) а * 0,001 = 7,3 * 10^11 * 10^-4 = 7,3 * 10^7
   в) а^2 * 0,000001 = (7,3 * 10^11 )^2 * 10^-7 =
= 7,3 ^2 * ( 10^11 )^2 * 10^-7 = 53.29* 10^11* 10^-7 =
   = 53.29* 10^4
4) а) = a/b + b/a = (a² + b²)/ab
   б) = 1/а* (1/а + 1/b) = 1/а* (a+b)/ab = (a+b)/a²b

<< < 9 1011 12 13 > >>