область определения функции - страница 10

1. Постройте график функции у=(х+3)^2. Укажите промежутки возрастания и убывания функции.
2. Постройте график функции у= - корень из х-4. Укажите ее область определения.
3. Постройте график функции у=- 4 / х + 1. Укажите координаты центра симметрии построенной гиперболы.
4. Постройте график функции у= модуль х -2. Укажите координаты точек пересечения графика с осями координат.

y=/x^2-3x+2/ (модуль)
1. Область определения
2. нули функции вроде х=1; х=2
3. промежуток знакопостоянства у(х)>o (?;1)U(2;?) y(x)<o (1;2)
4. промежутки возрастания и убывания. возрастает при хэ[3/2;?] убывает при хэ [-5/4;3/2]
5. наибольшее и наименьшее значения функции.
6. Область изменений

2. Нули ф-ии: х1=1, х2 = 2

3. Ф-ия неотрицательна на всей числовой оси: y>=0 при х прин.(-беск; беск)

4. у возр. при: х прин: [1; 1,5] v [2; беск).

    у убыв. при х прин: (-беск; 1] v [1,5; 2].

5. Наибольшего значения нет, наименьшее: у = 0 (при х = 1; 2)

6 Область значений: y: [0; беск)

Y=/x^2-3x+2/ (модуль) 1. Область определения 2. нули функции вроде х=1; х=2 3. промежуток знакопостоянства у(х)>o (?;1)U(2;?) y

2. Нули ф-ии: х1=1, х2 = 2

3. Ф-ия неотрицательна на всей числовой оси: y>=0 при х прин.(-беск; беск)

4. у возр. при: х прин: [1; 1,5] v [2; беск).

    у убыв. при х прин: (-беск; 1] v [1,5; 2].

5. Наибольшего значения нет, наименьшее: у = 0 (при х = 1; 2)

6 Область значений: y: [0; беск)  

Исследовать функцию
(обязательно по пунктам с вычислениями)
f(x)=2x^4+(8/3)x^3
1. Область определения
2. Область изменения
3. Чётность
4. Периодичность
5. Точки пересечения графика с осями координат
6. Промежутки знака постоянства
7. Промежутки возрастания, убывания
8. Точки экстремума, значение функции в этих точках
9. Поведение функции в окрестности "особых" точек при больших по модулю х (дополнительные точки)

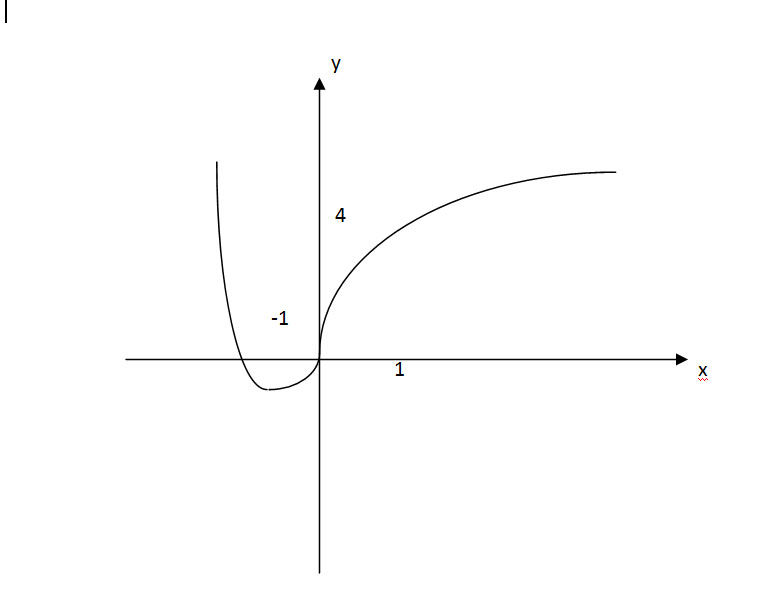
1) Найти множество значений функции: у=2х^2-4х+1

2) Указать область определения функции: у=корень квадратный х+3-корень квадратный 2х-10

3) Сумма модулей уравнения х^4+х^2-12=0 чему равна?

$$ x=-\frac{b}{2a} \\ x=\frac{4}{4}=1 $$

Подставляем единичку в функцию:

2*1-4*1+1=2-4+1=2-3=-1.

Ниже график функции не будет подыматься, следовательно, множество значений:

y∈{-1.+∞}.

2)$$ \sqrt{x+3}-\sqrt{2x-10} $$

Несмотря ни на что, под корнем НИКОГДА не должно быть отрицательное значение. Решаем 2 полноценных систем уравнения:

$$ \left \{ {{x+3\geq 0} \atop {2x-10\geq 0}}\right. \\ \left \{ {{x\geq-3} \atop {x\geq 5}}\right. $$

Но,3<5 ⇒x≥5.

D(f)=x≥5

3) Вы, наверно, имели ввиду сумму корней.

Проведем замену переменной:

$$ t=x^2 $$

Решаем квадратное уравнение:

$$ t^2+t-12=0 \\ D=1+48=49 \\ x_1=\frac{-1+7}{2}=3 \\ x_2=\frac{-1-7}{2}=-4 \\ $$

А теперь, решаем два уравнения:

$$ x^2=3 \\ x=\sqrt{3} \\ x^2=-4 \\ x_1=2i \\ x_2=-2i $$

Но, нежелательно в уравнение вставлять комплексные числа, т. е. второй вариант просто убираем. Получим единственный корень - √3.