область определения функции - страница 13

Функция y=lg(cosx+1). Нужно: 1. Найти область определения. 2. Является чётно или нечётной. 3. Является ли переодической. 4. Найти точки пересечения с осями координат. 5. Исследовать знак функции. 6. Найти вертикальные асимптоты. 7. Исследовать поведение функции на ∞. 8. Исследовать на возрастание и на убывание. 9. Точки перегиба. Выпуклость, вогнутость. Построить график функции не по точкам.

Решение: 1.cosx+1≥0 <=> x∈R

2.y(-x)=lg(cos(-x)+1)=lg(cosx+1)=y(x) - ф-ция чётная

3. Является, т. к. содержит периодическую ф-цию.

4. при х=0 y=lg2; y=0, при cosx+1=1 <=> cosx=0 <=> x=π/2+πk, k∈Z.

5. Ф-ция четная и при x=0 y>0, значит при x∈(-π/2+πk;π/2+πk), k∈Z y>0, а при

x∈(π/2+πk;π3/2+πk), k∈Z y<0.

6. Их нет.

7. Функция периодическая

8. На промежутке x∈(-π3/2+πk;πk), k∈Z фунция возрастает, а

на x∈(πk;π3/2+πk), k∈Z - убывает

9. Имеет максимум в точках x=2πk, k∈Z, минимум в точках x=π+2πk.

А как ещё строят графики? 0_0 И проги по точкам строят, и даже крутые математики. Иначе нельзя.
Выполнить исследование функции по следующей схеме:
1) найти область определения
2) проверить четность-нечетность функций
3) найти точки пересечения с осями координат
4) найти экстремумы и интервалы монотонности
5) найти точки перегиба и интервалы выпуклости и вогнутости
6) найти пределы функций при x (+)(-) бесконечности
7) построить график функции.
y=3x^3-15x^2+36x-5 ``Пожалуйста``

Решение: 1) Область определения: x ∈ (-∞; ∞).
2) Четность-нечетность:
$$ f(x) = 3x^3-15x^2+36x-5 \\ f(-x) = 3(-x)^3-15(-x)^2-36x-5 = -3x^3-15x^2-36x-5 \\ -f(x) = -3x^3+15x^2-36x+5 $$
Т. к. $$ f(x) = f(-x) $$ и $$ f(-x) = -f(x) $$, то функция является функцией общего вида.
3) Точки пересечения с Ox. Решим исходное уравнение при y = 0. (метод решения: Виета-Кардано)
Получим один корень: x = 0.148 - абсцисса точки пересечения графка с осью Ox. Координаты точки: (0.148; 0)
Точка пересечения с Oy. Найдем y, подставив в уравнение x = 0. Получим: y = -5. Координаты точки: (0,5).
4) Так как функция кубическая, то точек экстремума не имеет.
5) Первая производная.
$$ f’(x) = 9x^2-30x+36 $$
2. Вторая производная.
$$ f’’(x) = 18x-30 $$
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
$$ 18x-30 = 0 $$
Откуда точка перегиба:
x = 5/3
На промежутке: (-∞ ;5/3)
$$ f’’(x) < 0 $$
Значит, функция выпукла.
На промежутке (5/3; ∞)
$$ f’’(x) > 0 $$
Значит, функция вогнута.
6) $$ \lim_{x \to \infty} 3x^3-15x^2+36x-5 = \infty \\ \lim_{x \to -\infty} 3x^3-15x^2+36x-5 = -\infty $$
7(график в приложениях)
Как мог. Работа объемная, конечно)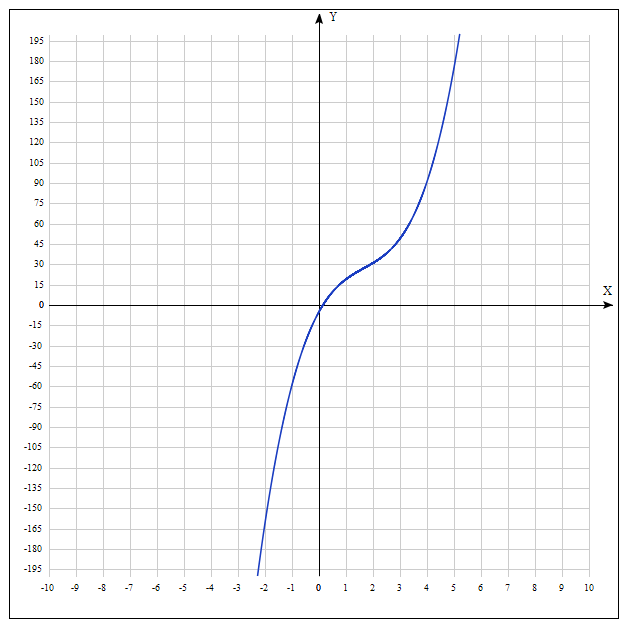
Построение графика функции
1. Найти область определения.
2. Найти точки пересечения графика функции с осями координат.
3. Исследовать функцию на четность и нечетность
4. Найти интервалы знака-постоянства функции
5. Исследуйте функцию на периодичность
6. Найдите интервалы монотонности функции
7. Исследовать функцию на экстремум и значении функции в этих точках
8. Найдите 1-2 дополнительные точки для уточнения графика функции.
Y=-X^4/4+X^2
Нужно(4-8) Кто сделает отмечу как лучший

Решение: Исследование с рассуждениями проведём по плану.
Нам потребуется координатная плоскость примерно +/- 3 по оси Х и от -2 до 10 по оси У
1. Область определения.
На вид никаких ограничений на аргумент Х - нет.
Нет деления на ноль и нет неопределенности типа 0/0.
Х⊂ (-∞;+∞) или Х ⊂ R - все числа без исключения.
2. Точки пересечения с осями.
Подставим значение Х=0 и вычисляем
Y(0) = 0 - или при Х=0 Y=0 - одна точка пересечения - начало координат.
Отмечаем точку пересечения на координатной плоскости.
3. Исследовать на четность и нечетность.
Видим, что все степени при аргументе - четные (это 4 и 2) - значит и функция тоже четная. Но, по определению четной функции - У(-х) = У(+Х)
Вычисляем - У(-2) = У(+2) = 8.
Значения равны - функция четная.
Отмечаем на координатной плоскости две точки А(-2;8) и В(2;8).
4. Интервалы знака-постоянства - всегда положительна
5. Периодичность - нет периода. Обычно это у тригонометрических функций.
6. Исследование на экстремумы.
Для этого необходимо проанализировать первую производную функции.
Где она отрицательна - функция убывает, где положительна - возрастает, где равна 0 - точка экстремума. Вычисляем первую производную функции.
Y’ (x) = 4*(1/4)*x³ + 2*x = x³+2x = x*(x²+1) =0
Анализируем -
а) равна 0 при Х=0 - точка экстремума
б) Y’ (-1) = - 3 - отрицательна - "наша" - Y - убывает - отмечаем на графике, но "в уме"
в) Y’(+1) = 3 - положительна - "наша" - возрастает - отмечаем.
Делаем вывод, что в точке Х=0 - минимум.
Значение в точке экстремума равно
Ymin = Y(0) = 0; - точка уже отмечена на плоскости.
7. Исследование на монотонность или выпуклость- вогнутость.
Где она равна 0. там точка перегиба. Где отрицательна - выпуклая, где положительная - вогнутая.
Для этого потребуется вторая производная функции.
Y’(x) =3*x² + 2 - всегда положительна - "наша" Y-функция - всегда вогнутая.
8. Вычисляем дополнительные точки для построения графика
Y(1) = Y(-1) = 1 - ставим на графике.
Y(1/2) = Y(-1.2) = 0.2656 ~ 0.25 = 1/4 - строим еще две точки.
И соединяем плавной-плавной, но кривой линией все точки.
Получили график, который можно сравнить с таким же графиком, построенным на компьютере.
Исследование функции закончено.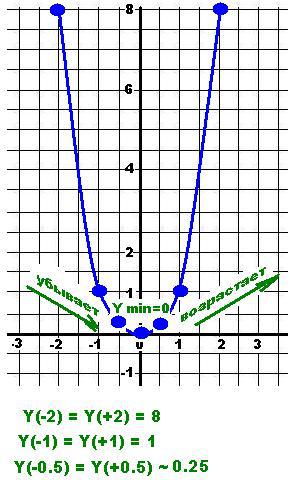
Дана функция:y= 4x^3+6x^2
1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями координат.
3. Исследовать функцию на четность и нечетность.
4. Найти интервалы знака постоянства функции.
5. Найти интервалы монотонности функции.
6. Исследовать функцию на экстремум и значение функции в заданной точке.

Решение: Y=4x³+6x²
1. определена при всех х
2. х=0⇒у=0 у=0⇒х=0 одна точка пересечения в начале координат.
3. y(-x)=-4x³+6x² ни четная ни нечетная
4. y=x²(4x+6) функция больше 0 при 4x+6 >0 x> -1.5 b y<0 x<-1.5
5. y’=12x²+12x=12x(x+1)
-1- 0 -
+ - +
монотонно возрастает х∈(-∞,1)∪(0,∞)
убывает х∈(-1,0 )
6. y’=0 12x(x+1)=0 x=0 переход от убывания к возрастанию, локальный минимум у=0
х=-1 переход от возрастания ф-ии к ее убыванию - локальный максимум. у=-4+6 у=2
Y = 2*x^3+3*x^2-12*x+2
1. найти область определения функции
2. проверить функцию на четность и не четность
3. исследовать функцию на периодичность
4. найти точки пересечения графика функции с осями координат
5. исследовать функцию на монотонность и найти точки эктрениума
6. построить график

Решение: 1. Область определения - вся числовая ось ( нет особых точек).
2. Ф-я не четная и не нечетная т. к. f(x) !=f(-x) и f(x) != -f(x)
3. Ф-я непереодическая
4. Найдем корни - это точки пересечения с осью Х (-3,369; 0,175; 1,694)
(примечание: корни могут быть найдены только численными методами, аналитического выражения нет). y(0)=2 (пересечение с осью У)
5. Для нахождения точек экстремума берем 1-ю и 2-ю производные, приравниваем их 0. По 1-й производной 6x^2+6x-12 (корни = 1; -2) Экстремумы в точках: 1;-2.
Так как 2-я производная (12х+6) в (.)-2 отрицательна, то в (.) -2 имеем максимум,
так как 2-я производная в (.) 1 положительна. то в (.) 1 имеем минимум.
Приравняв 0 2-ю производную, получаем точку перегиба = (-0.5).
Итак, функция возрастает на интервале (-беск,2), убывает в интервале (-2,1) и возрастает в интервале (1,+беск).

<< < 11 1213 14 15 > >>