область определения функции - страница 15

Построить график функции y = (2x^2+1)/x^2 по следующему алгоритму:
1) Область определения функции
2) Непрерывность функции и её четность(lim y =? при x-> +- ∞)
3) Пересечение с осями координат и точки разрыва (найти точки разрыва с помощью пределов)
4) Асимптоты (вертикальные и наклонные, найти их через пределы)
5) Возрастание, убывание, экстремумы функции(через достаточные условия)
6) Выпуклость, вогнутость и перегибы графика
7) Построить сам график со всеми асимптотами

Решение: Дано: $$ y = \frac{2x^2+1}{x^2} $$ ;
Исследовать функцию и построить график.
Решение:
1) Функция не определена при обращении в ноль знаменателя, т. е. x ≠ 0.
D(f) ≡ R \ {0} ≡ $$ ( -\infty ; 0 )U( 0 ; +\infty ) $$ ;
2) В функции встречаются только чётные степени аргумента, а значит она чётная. Докажем это:
$$ y(-x) = \frac{ 2(-x)^2 + 1 }{ (-x)^2 } = \frac{2x^2+1}{x^2} = y(x) $$ ;
Найдём первую производную функции y(x) :
$$ y’(x) = ( \frac{2x^2+1}{x^2} )’ = ( \frac{ 2x^2 }{x^2} + \frac{1}{x^2} )’ = ( 2 + x^{-2} )’ = -2 x^{-3} $$ ;
$$ y’(x) = -\frac{2}{x^3} $$ ;
При x = 0, производная y’(x) – не определена, как и сама функция, при всех остальных значениях аргумента функция и её первая производная определены и конечны, а значит функция непрерывная на всей области определения D(f) – на всей числовой прямой, кроме ноля.
3) Функция не определена при x = 0. Это точка разрыва. При этом её значение стремится к положительной бесконечности, что легко доказать:
$$ \lim_{x \to 0} y(x) = \lim_{x \to 0} \frac{2x^2+1}{x^2} = \lim_{x \to 0} 2 + \lim_{x \to 0} \frac{1}{x^2} = 2 + \infty = +\infty $$ ;
Если приравнять функцию к нолю, получим:
$$ y(x) = 0 $$ ;
$$ \frac{2x^2+1}{x^2} = 0 $$ ;
$$ 2 + \frac{1}{x^2} = 0 $$ ;
$$ ( \frac{1}{x} )^2 = -2 $$ – что невозможно ни при каких действительных значениях аргумента;
Значит, никаких пересечений графика с осями координат нет.
4. Найдем асимптоты y(x).
По найденному в (3) пределу, ясно, что линия x = 0 – является вертикальной двухсторонней асимптотой графика функции y(x).
Посмотрим, что происходит с функцией y(x) при устремлении аргумента к ± $$ \infty $$ :
$$ \lim_{x \to \infty} y(x) = \lim_{x \to \infty} \frac{2x^2+1}{x^2} = \lim_{x \to \infty} 2 + \lim_{x \to \infty} \frac{1}{x^2} = 2 + 0 = 2 $$ ;
Значит, уходя на ∞ обоих знаков график функции y(x) имеет двунаправленную горизонтальную асимптоту y = 2 ;
Наклонных асимптот нет, и не может быть, так как есть горизонтальные с обеих сторон.
5. Первая производная функции y(x) :
$$ y’(x) = -\frac{2}{x^3} $$ – положительна при отрицательных значениях аргумента и отрицательна при положительных х ;
Значит, функция возрастает на $$ ( -\infty ; 0 ) $$ и убывает на $$ ( 0 ; +\infty ) $$ ;
Уравнение $$ y’(x) = 0 $$ т. е. $$ y’(x) = -\frac{2}{x^3} $$ – не имеет решений, а значит, у функции нет экстремумов, т. е. конечных локальных минимумов или максимумов.
6. Найдём вторую производную функции y(x) :
$$ y’’(x) = (y’(x))’ = ( -\frac{2}{x^3} )’ = -2 ( x^{-3} )’ = -2*(-3)*x^{-4} $$ ;
$$ y’’(x) = \frac{6}{x^4} > 0 $$ при любых значениях аргумента ;
В силу общей положительности второй производной – график функции всегда «улыбается», т. е. он вогнут, или, говоря иначе: он закручивается против часовой стрелки на всём своём протяжении при проходе по числовой оси аргументов слева направо.
Поскольку выгнутость повсеместна, то и точек перегиба не может быть. И их нет, соответственно.
7.
При х = ± 1 : : : y(x) = 3 ;
При х = ± 2 : : : y(x) = 2.25 ;
При х = ± 1/2 : : : y(x) = 6 ;
Строим график:

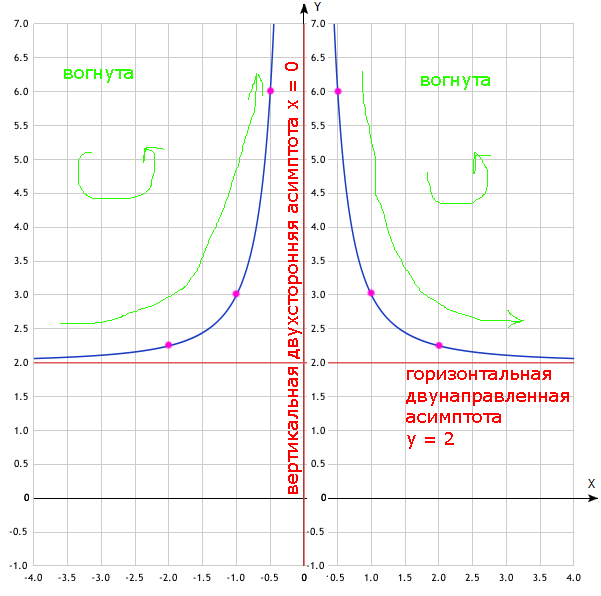
$Дано y frac x x Исследовать функцию и построить график.Решение Функция не определена при обращении в ноль знаменателя т. е. x .D f R - infty U infty В функции встречаются тол...$
Построить график функции y = (2x^2+1)/x^2 по следующему алгоритму:
1) Область определения функции
2) Непрерывность функции и её четность(lim y =? при x-> +- ∞)
3) Пересечение с осями координат и точки разрыва (найти точки разрыва с помощью пределов)
4) Асимптоты (вертикальные и наклонные, найти их через пределы)
5) Возрастание, убывание, экстремумы функции(через достаточные условия)
6) Выпуклость, вогнутость и перегибы графика
7) Построить сам график со всеми асимптотами

Решение: Дано: $$ y = \frac{2x^2+1}{x^2} $$ ;
Исследовать функцию и построить график.
Решение:
1) Функция не определена при обращении в ноль знаменателя, т. е. x ≠ 0.
D(f) ≡ R \ {0} ≡ $$ ( -\infty ; 0 )U( 0 ; +\infty ) $$ ;
2) В функции встречаются только чётные степени аргумента, а значит она чётная. Докажем это:
$$ y(-x) = \frac{ 2(-x)^2 + 1 }{ (-x)^2 } = \frac{2x^2+1}{x^2} = y(x) $$ ;
Найдём первую производную функции y(x) :
$$ y’(x) = ( \frac{2x^2+1}{x^2} )’ = ( \frac{ 2x^2 }{x^2} + \frac{1}{x^2} )’ = ( 2 + x^{-2} )’ = -2 x^{-3} $$ ;
$$ y’(x) = -\frac{2}{x^3} $$ ;
При x = 0, производная y’(x) – не определена, как и сама функция, при всех остальных значениях аргумента функция и её первая производная определены и конечны, а значит функция непрерывная на всей области определения D(f) – на всей числовой прямой, кроме ноля.
3) Функция не определена при x = 0. Это точка разрыва. При этом её значение стремится к положительной бесконечности, что легко доказать:
$$ \lim_{x \to 0} y(x) = \lim_{x \to 0} \frac{2x^2+1}{x^2} = \lim_{x \to 0} 2 + \lim_{x \to 0} \frac{1}{x^2} = 2 + \infty = +\infty $$ ;
Если приравнять функцию к нолю, получим:
$$ y(x) = 0 $$ ;
$$ \frac{2x^2+1}{x^2} = 0 $$ ;
$$ 2 + \frac{1}{x^2} = 0 $$ ;
$$ ( \frac{1}{x} )^2 = -2 $$ – что невозможно ни при каких действительных значениях аргумента;
Значит, никаких пересечений графика с осями координат нет.
4. Найдем асимптоты y(x).
По найденному в (3) пределу, ясно, что линия x = 0 – является вертикальной двухсторонней асимптотой графика функции y(x).
Посмотрим, что происходит с функцией y(x) при устремлении аргумента к ± $$ \infty $$ :
$$ \lim_{x \to \infty} y(x) = \lim_{x \to \infty} \frac{2x^2+1}{x^2} = \lim_{x \to \infty} 2 + \lim_{x \to \infty} \frac{1}{x^2} = 2 + 0 = 2 $$ ;
Значит, уходя на ∞ обоих знаков график функции y(x) имеет двунаправленную горизонтальную асимптоту y = 2 ;
Наклонных асимптот нет, и не может быть, так как есть горизонтальные с обеих сторон.
5. Первая производная функции y(x) :
$$ y’(x) = -\frac{2}{x^3} $$ – положительна при отрицательных значениях аргумента и отрицательна при положительных х ;
Значит, функция возрастает на $$ ( -\infty ; 0 ) $$ и убывает на $$ ( 0 ; +\infty ) $$ ;
Уравнение $$ y’(x) = 0 $$ т. е. $$ y’(x) = -\frac{2}{x^3} $$ – не имеет решений, а значит, у функции нет экстремумов, т. е. конечных локальных минимумов или максимумов.
6. Найдём вторую производную функции y(x) :
$$ y’’(x) = (y’(x))’ = ( -\frac{2}{x^3} )’ = -2 ( x^{-3} )’ = -2*(-3)*x^{-4} $$ ;
$$ y’’(x) = \frac{6}{x^4} > 0 $$ при любых значениях аргумента ;
В силу общей положительности второй производной – график функции всегда «улыбается», т. е. он вогнут, или, говоря иначе: он закручивается против часовой стрелки на всём своём протяжении при проходе по числовой оси аргументов слева направо.
Поскольку выгнутость повсеместна, то и точек перегиба не может быть. И их нет, соответственно.
7.
При х = ± 1 : : : y(x) = 3 ;
При х = ± 2 : : : y(x) = 2.25 ;
При х = ± 1/2 : : : y(x) = 6 ;
Строим график:

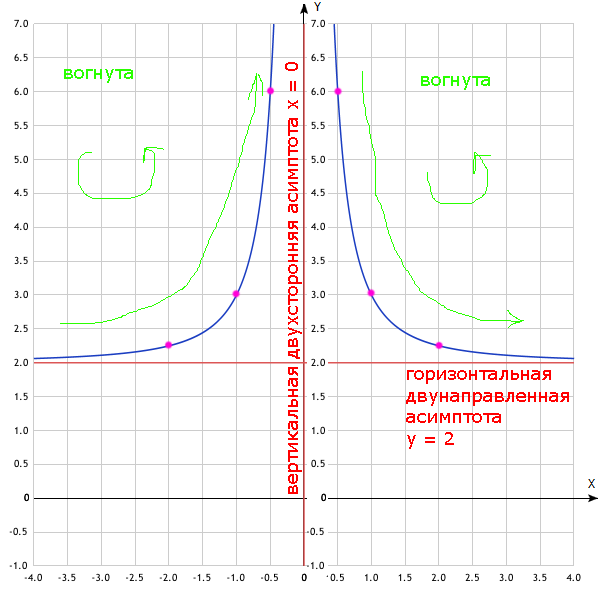
$Дано y frac x x Исследовать функцию и построить график.Решение Функция не определена при обращении в ноль знаменателя т. е. x .D f R - infty U infty В функции встречаются тол...$
Y=x^2+3/x^2+1 1) найти область определения 2) найти точки пересечения графика с осями координат( если это возможно) 3) определить чётность и нечётность функции 4) определить промежутки монотонности 5) экстремумы функции 6) найти интервалы выпуклости и точки перегиба 7) график

Решение: Y=(x²+3)/(x²+1)
D(y)∈(-∞;∞)
y(-x)=(x²+3)/(x²+1) четная
x=0 y=3
Точка пересечения с осями (0;3)
y’=[2x(x²+1)-2x(x²+3)]/(x²+1)²=2x(x²+1-x²-3)/(x²+1)²=-4x/(x²+1)²=0
x=0
+ _
-(0)-
возр max убыв
ymax=3
y``=[-4(x²+1)²+4x*2x*2(x²+1)]/(x²+1)^4=-4(x²+1)(x²+1-16x²)/(x²+1)^4=4(15x²-1)/(x²+1)³=0
15x²-1=0
15x²=1
x²=1/15
x=-1/√15≈-0,3
x=1/√15≈0,3
y(-1/√15)=y(1/√15)=(1/15+3):(1/15+1)=46/15*15/16=46/16=23/8≈3
(-1/√15;23/8) U (1/√15;23/8)-точки перегиба
+ _ +
-(-1/√15)-(1/√15)-
вог вниз выпук вверх вогн вниз
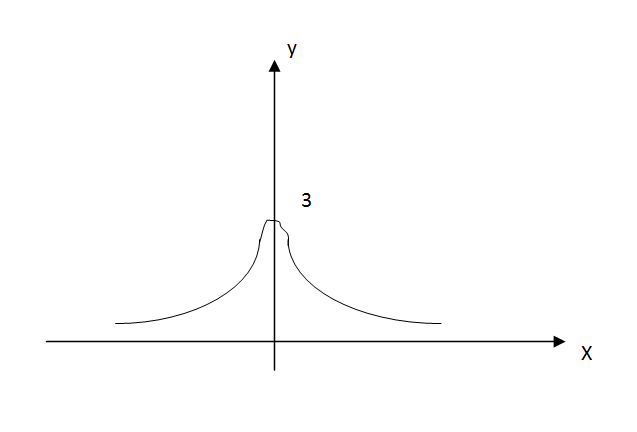
Y=x^3-9/2*x^2+6x-2 найти
1) область определения
2) выяснить не является ли функция четной, нечетной или периодичной,
3) найти точки пересечения графика с осями координат если они есть
4) найти асимптоты графика функции,
5) найти промежутки монотонности и ее экстремумы,
6) найти промежутки выпуклости и точки перегиба функции
7) построить график используя полученные результаты исследования

Решение: ДАНО
Y = x³ - 4.5*x²+6x-2.
ИССЛЕДОВАНИЕ ФУНКЦИИ.
1. Область определения - R - все действительные.
Или Х∈(-∞,+∞) - непрерывная. Разрывов нет.
2. Пересечение с осью абсцисс - ось Х -
х1 = 1/2 и х2 = 2
3. Пересечение с осью ординат - ось У - У(0) = 2.
4. Поведение в бесконечности.
Y(-∞) = -∞, Y(+∞) = +∞.
5. Исследование на четность.
Y(-x) ≠ Y(x) - функция ни четная ни нечетная.
6. Производная функции
Y’ = 3x²-9x+6 = 3*(x-1)(x-2). Корни - х1= 1 и х2 = 2.
7. Монотонность.
Возрастает - Х∈(-∞,1]
Максимум - Y(1) = 1/2 = 0.5
Убывает - Х∈[-1.2]
Минимум - Y(2) = 0
Возрастает - Х∈[2.+∞)
8. Вторая производная
Y" = 6x - 9
9. Точка перегиба - Y"=0 при X= 2/3.
10. Построение графика - .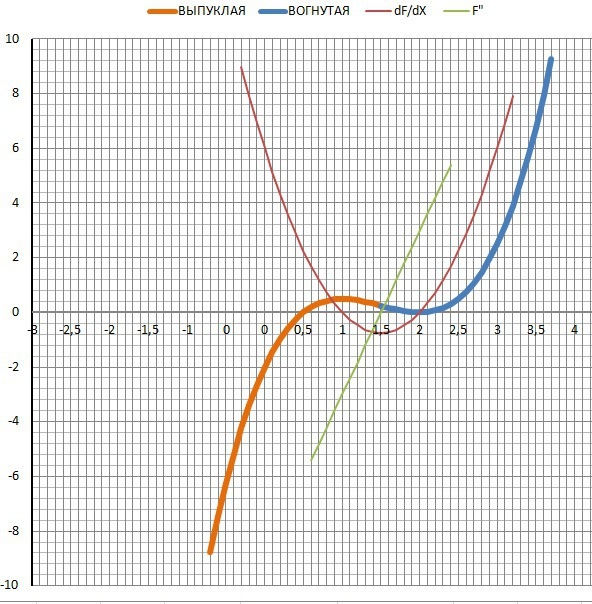
Исследовать функцию y=x^3+3x по плану 1. Найти область определения функции D(y)
2. Определить четность-нечетность функции
3. Нули функции(точки пересечения графика с осями координат)
4. Промежутки монотоности
5. Точки экстремума
6. Построение графика функции, дополнительные точки

Решение: 1.D(y)=(-∞;+∞)
2. y(x)=3x-x^3
y(-x)=x^3-3x =>> функция нечетная
3. ось абсцисс - 3x-x^3=0 |*(-1)
x^3-3x=0
x(x^2-3)=0
x=0 x=+-sqrt(3)
ось ординат - x=0 y=0
4. x=0 y=0
5.y=x^3-3x
y’=3x^2-3
3x^2-3=0
x^2=1
x=+-1
Возрастает от (-∞;-1)(1;+∞)
Убывает на промежутке (-1;1)
5. точка максимума- х=0
точка минимума- х=2/3
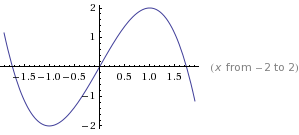
6.

<< < 13 1415 16 17 > >>