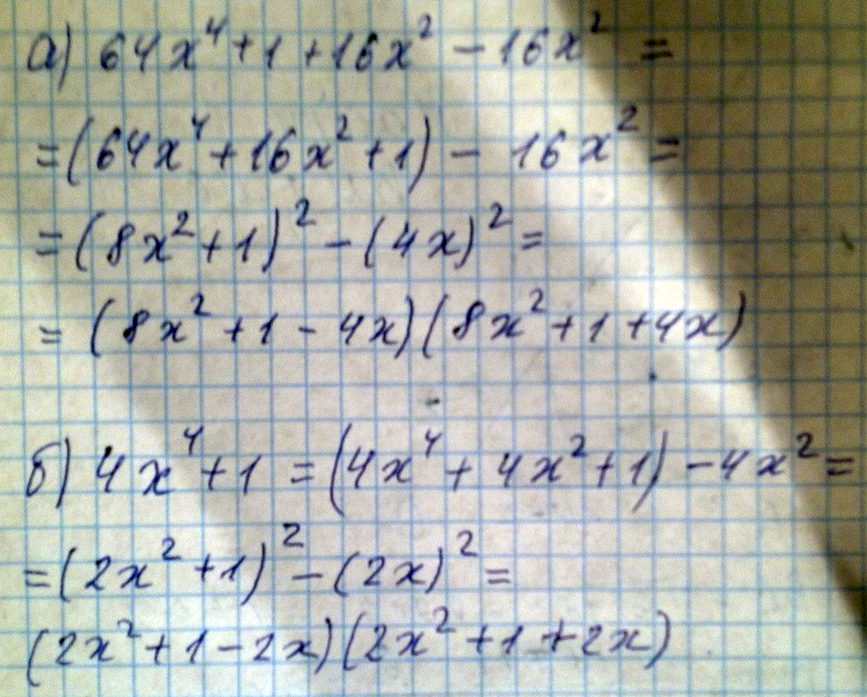разложить многочлен на множители - страница 13

Разложите на множители многочлен
1) xyz+4xz+3xy+12x=
2) 2a+a^2+2a^3+a^4=
3) m^3+m^2n-m^2a-mna=
4) b^4-b^3+b^2-b=

xy(z+3)+ 4x(z+3)=(xy+4x)(z+3)

2. также первый с третьим, 2 с 4.

2a+a^2+2a^3+a^4=2a(1+a^2)+a^2(1+a^2)=(2a+a^2)(1+a^2)

3.1 с 3, 2 с 4.

m^3+m^2n-m^2a-mna=m^2(m-a)+mn(m-a)=(m^2+mn) (m-a)

4.1 со 2, 3 с 4.

b^4-b^3+b^2-b=b^3(b-1)+b(b-1)=(b^3+b)(b-1)

1) xyz+4xz+3xy+12x=xz(y+4)+3x(y+4)=(y+4)^2*(xz+3x)
2) 2a+a^2+2a^3+a^4=a(2+a)*a^3(2+a)=(a+a^3)* (2+a) ^2
3) m^3+m^2n-m^2a-mna=m^2(m+n)-ma(m+n)=(m^2-ma)*(m+n)^2
4) b^4-b^3+b^2-b=b^3(b-1)*b(b-1)=(b^3+b)*(b-1)^2

Разложите на множители многочлен:
1/ 7x-7y+bx-by=
2/ pq-x-px+q=
3/ 2cx-cy-6x+3y=
4/ 56pq-1-7q+8p=

2) $$ pq-x-px+q=(pq+q)+(-px-x)=(pq+q)-(px+x)=\\=q(p+1)-x(p+1)=(p+1)(q-x) $$

3) $$ 2cx-cy-6x+3y=(2cx-cy)+(-6x+3y)=\\=(2cx-cy)-(6x-3y)=c(2x-y)-3(2x-y)=(2x-y)(c-3) $$

4) $$ 56pq-1-7q+8p=(56pq+8p)+(-7q-1)=\\=(56pq+8p)-(7q+1)=8p(7q+1)-1(7q+1)=(7q+1)(8p-1) $$

разложите на множители многочлен
x³+x²+x+1
y∧5-y³-y²+1
a∧4+2a³-a-2
b∧6-3b∧4-2b²+6
a²-ab-8a+8b
ab-3b+b²-3a
11x-xy+11y-x²
kn-mn-n²+mk
2) разложите на множители многочлен
ab-8a-bx+8x
ax-b+bx-a
ax-y+x-ay
ax-2bx+ay-2by
3) разложите на множители многочлен
mx+my+6x+6y
9x+ay+9y+ax
7a-7b+an-bn
ax+ay-x-y
1-bx-x+b
xy+2y-2x-4

-

Задание № 1

$$ x^{3}+x^{2}+x+1=(x^{3}+x^{2})+(x+1)=\\=x^{2}(x+1)+(x+1)=x^{2}(x+1)+1(x+1)=(x+1)(x^{2}+1) $$

$$ y^{5}-y^{3}-y^{2}+1=(y^{5}-y^{3})+(-y^{2}+1)=(y^{5}-y^{3})-(y^{2}-1)=\\=y^{3}(y^{2}-1)-(y^{2}-1)=y^{3}(y^{2}-1)-1(y^{2}-1)=(y^{2}-1)(y^{3}-1) $$

$$ a^{4}+2a^{3}-a-2=(a^{4}-a)+(2a^{3}-2)=\\=a(a^{3}-1)+2(a^{3}-1)=(a^{3}-1)(a+2) $$

$$ b^{6}-3b^{4}-2b^{2}+6=(b^{6}-2b^{2})+(-3b^{4}+6)=\\=(b^{6}-2b^{2})-(3b^{4}-6)=b^{2}(b^{4}-2)-3(b^{4}-2)=(b^{4}-2)(b^{2}-3) $$

$$ a^{2}-ab-8a+8b=(a^{2}-ab)+(-8a+8b)=\\=(a^{2}-ab)-(8a-8b)=a(a-b)-8(a-b)=(a-b)(a-8) $$

$$ ab-3b+b^{2}-3a=(ab+b^{2})+(-3b-3a)=\\=(ab+b^{2})-(3b+3a)=(ab+b^{2})-(3a+3b)= b(a+b)-3(a+b)=(a+b)(b-3) $$

$$ 11x-xy+11y-x^{2}=(11x+11y)+(-xy-x^{2})=\\=(11x+11y)-(xy+x^{2})=11(x+y)-x(y+x)=(x+y)(11-x) $$

$$ kn-mn-n^{2}+mk=(kn-n^{2})+(mk-mn)=\\=n(k-n)+m(k-n)=(k-n)(n+m) $$

Задание № 2

$$ ab-8a-bx+8x=(ab-bx)+(-8a+8x)=\\=(ab-bx)-(8a-8x)=b(a-x)-8(a-x)=(a-x)(b-8) $$

$$ ax-b+bx-a=(ax+bx)+(-b-a)=(ax+bx)-(b+a)=\\=(ax+bx)-(a+b)=x(a+b)-(a+b)=x(a+b)-1(a+b)=(a+b)(x-1) $$

$$ ax-y+x-ay=(ax-ay)+(-y+x)=(ax-ay)+(x-y)=\\=a(x-y)+(x-y)=a(x-y)+1(x-y)=(x-y)(a+1) $$

$$ ax-2bx+ay-2by=(ax+ay)+(-2bx-2by)=\\=(ax+ay)-(2bx+2by)=a(x+y)-2b(x+y)=(x+y)(a-2b) $$

Задание № 3

$$ mx+my+6x+6y=(mx+my)+(6x+6y)=m(x+y)+6(x+y)=\\=(x+y)(m+6) $$

$$ 9x+ay+9y+ax=(9x+9y)+(ay+ax)=\\=(9x+9y)+(ax+ay)=9(x+y)+a(x+y)=(x+y)(9+a) $$

$$ 7a-7b+an-bn=(7a-7b)+(an-bn)=\\=7(a-b)+n(a-b)=(a-b)(7+n) $$

$$ ax+ay-x-y=(ax+ay)+(-x-y)=(ax+ay)-(x+y)=\\=a(x+y)-(x+y)=a(x+y)-1(x+y)=(x+y)(a-1) $$

$$ 1-bx-x+b=(1+b)+(-bx-x)=\\=(1+b)+(-x-bx)=(1+b)-(x+bx)=(1+b)-x(1+b)=1(1+b)-x(1+b)=(1+b)(1-x) $$

$$ xy+2y-2x-4=(xy+2y)+(-2x-4)=\\=(xy+2y)-(2x+4)=y(x+2)-2(x+2)=(x+2)(y-2) $$

разложите на множители многочлен:
a) 64x^4+1+16x^2-16x^2
б)4x^4+1

$$ 64x^4+1+16x^2-16x^2=64x^2+16x^2+1-16x^2= \\ = (8x^2+1)-(4x)^2=(8x^2+1-4x^2)(8x^2+4x+1) $$

воспользовался формулами:

$$ 1) \ a+b=b+a \\ 2) \ a^2+2ab+b^2=(a+b)^2 \\ 1) a^2-b^2=(a-b)(a+b) $$

второе:

$$ 4x^4+1=4x^4+4x^2+1-4x^2=(2x^2+1)^2-(2x)^2= \\ = (2x^2-2x+1)(2x^2+2x+1) $$

воспользовался формулами:

$$ \rm \ ECLI \ \ a=b, TO \ \ a \pm c=b\pm c $$

и из предыдущего решения

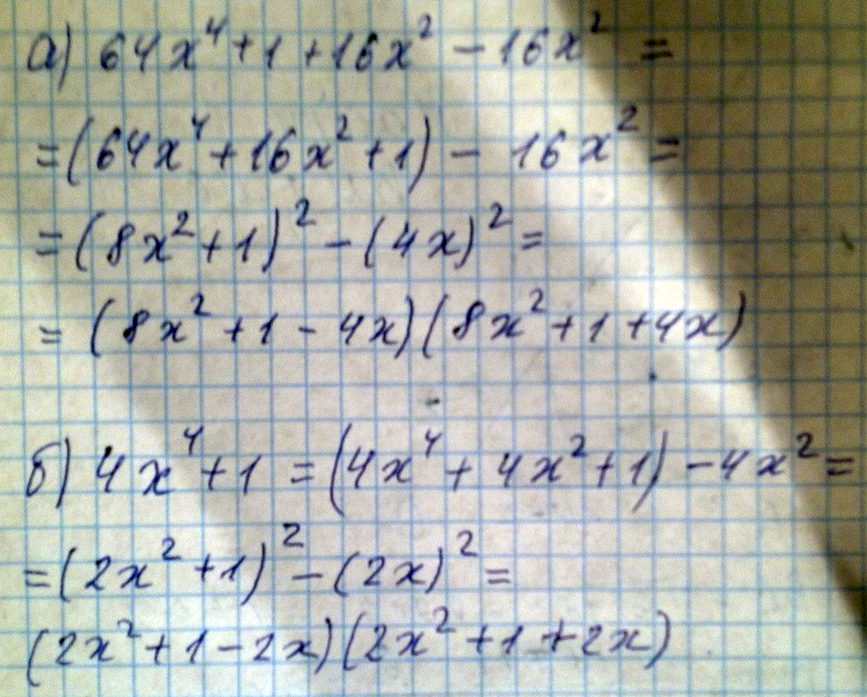
Разложите на множители многочлен^
а) 16a^2-225b^2
б) 121х^2+9y^2-66xy
в) 1/8x^3-125a^3
г) a^3-6a^2*x+12ax^2-8x^3
д) a^5-1/32b^5