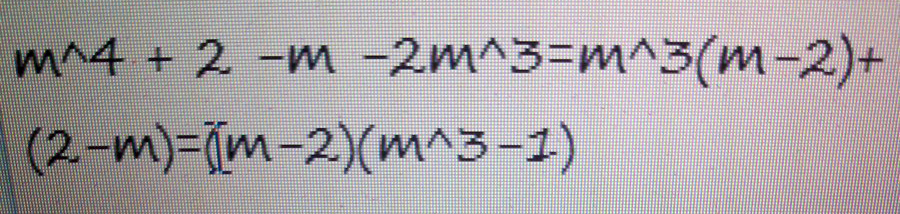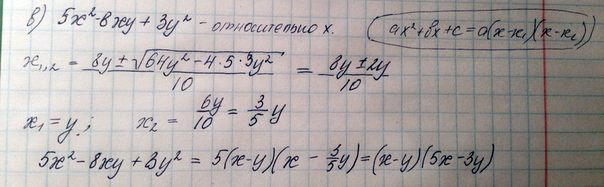многочлен »

разложить многочлен на множители - страница 11

  • Помогите разложить многочлен на множители \(x^4-10x^3+38x^2-65x+40=0\)


    Решение: $$ x^4-10x^3+38x^2-65x+40=0\\(ax^2+bx+c)(dx^2+ex+f)=\\=adx^4+(ae+bd)x^3+(af+be+cd)x^2+(bf+ce)x+cf\\\begin{cases}ad=1\\ae+bd=-10\\af+be+cd=38\\bf+ce=-65\\cf=40\end{cases}\Rightarrow\begin{cases}a=d=1\\e+b=-10\\8+be+5=38\\5b+8e=-65\\c=8\\f=5\end{cases}\Rightarrow\begin{cases}a=1\\b=-5\\c=8\\d=1\\e=-5\\f=5\end{cases}\\x^4-10x^3+38x^2-65x+40=(x^2-5x+8)(x^2-5x+5)\\x^2-5x+8=0\\D=25-4\cdot8=25-32=-7<0\;pew.\;HET\\x^2-5x+5=0\\D=25-4\cdot5=5\\x_1=\frac{5-\sqrt5}2,\;x_2=\frac{5+\sqrt5}2 \\ x^4-10x^3+38x^2-65x+40=(x^2-5x+8)\left(x-\frac{5+\sqrt5}2\right)\left(x-\frac{5-\sqrt5}2\right) $$

  • Как разложить многочлен на множители m^4+2-m-2m^3


    Решение: $$ m^{2}+2-m-2m^{3} \\ (m^{2}-m)+(2-2m^{3}) \\ m(m-1)+2(1-m^{3} ) $$

    Это и есть разложение на множители, там конечно же если тебе нужно продолжить просто вторую скобку раскрой как разность кубов

    m -m- m m -m - m m m- -m Это и есть разложение на множители там конечно же если тебе нужно продолжить просто вторую скобку раскрой как разность кубов...

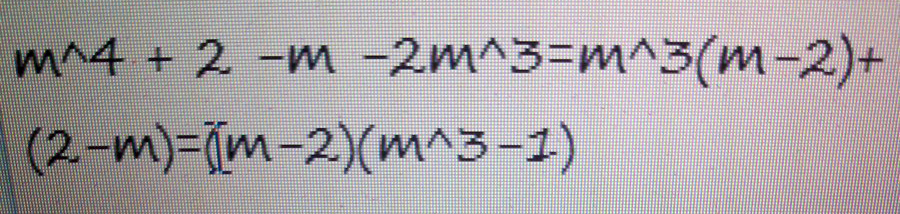
  • 1. Разложить многочлен на множители:
    а) а4 –18а2 + 81;
    б) а5 + а3 – а2 –1;
    в) а5 +3а4 – 4а3 – 12а2;
    г) а4 + 2а3 – 2а –1;
    д) а4 + а2 + 1.
    2. Решить уравнение разложением на множители:
    а) 9х3 – 18х2 = х – 2;
    б) у3 – у2 = у – 1;
    в) х3 – 3х2 – 3х + 1 = 0;
    г) х4 – 2х3 + 2х – 1 = 0;
    д) х5 + 5х3 – 6х2 = 0.


    Решение: №1
    а) а4 –18а2 + 81=(a2-9)^2=(a2-9)(a2-9);
    б) а5 + а3 – а2 –1=a2(a3-1)+a3-1=(a3-1)(a2+1);
    в) а5 +3а4 – 4а3 – 12а2=;a4(a+3)-3a2(a+3)=(a+3)(a4-3a2);
    г) а4 + 2а3 – 2а –1=(a2+1)(a2-1)+2a(a2-1)=(a2-1)(a2+1+2a;

    д) а4 + а2 + 1= а4 + 2а2 + 1-a2=(a2+1)2 -a2=(a2-a+1)(a2+a+1).

    № 2

    а) 9х3 – 18х2 = х – 2
    9x2(x-2)-(x-2)=0
    (x-2)(9x2-1)=0
    (x-2)(3x-1)(3x+1)=0
    x-2=0 ; 3x-1=0 ; 3x+1=0
    x=2 ; x=1/3 ; x=-1/3
    б) у3 – у2 = у – 1;
    y2(y-1)-(y-1)=0
    (y-1)(y2-1)=0
    (y-1)(y-1)(y+1)=0
    y-1=0 y+1=0
    y=1 y=-1
    в) х3 – 3х2 – 3х + 1 = 0;
    х3+1 – 3х(x +1) = 0;
    (x+1)(x2-x+1)-3x(x+1)=0
    (x+1)(x2-x+1-3x)=0
    (x+1)(x2-4x+1)=0
    x+1=0 x2-4x+1=0
    x=-1 D=16-4*1=12
    x=-1 x=2±√3

    г) х4 – 2х3 + 2х – 1 = 0
    x4-1 -2x(x2-1)=0
    (x2-1)(x2+1)-2x(x2-1)=0
    (x2-1)(x2+1-2x)=0
    x2-1=0 x2-2x+1=0
    (x-1)(x+1)=0 D=4-4*1=0
    x=±1 x=-b/2a=1
    д) х5 + 5х3 – 6х2 = 0
    x2(x3+5x-6)=0
    x2=0 | x3+5x-6=0
    x=0 | x3-1+5x-5=0
    x=0 | (x-1)(x2+x+1)+5(x-1)=0
    x=0 | (x-1)(x2+x+6)=0
    x=0 | x-1=0 | x2+x+6=0
    x=0 | x=1 | D=1-4*6=-23 - Нет корней.

  • разложить многочлен на множители:
    а)7x^2+5xy-12y^2
    б)5x^2-8xy+3y^2


    Решение: $$ А)  a=7, b=5y, c= -12y^{2} \\ D= 25y^2+ 4\cdot7\cdot 12y^{2} = 361y ^{2};\\ x_1= \frac{-5y- \sqrt{ 361y^{2} } }{14} =  \frac{-5y-19y}{14} =\\ =  \frac{24y}{14} = -\frac{12y}{7} \\ ;x2  = \frac{-5y+19y}{14} = y \\ 7 x^{2} + 5xy - 12 \\ y^{2} = (x-y)(7x+12y)$$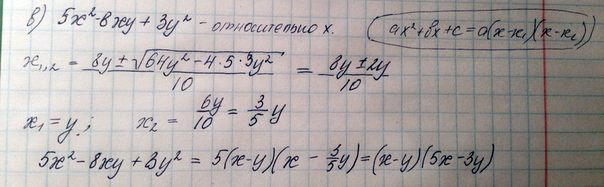А   a b y c - y D y cdot cdot y y x   frac - y- sqrt y   frac - y- y   frac y - frac y x   frac - y y y x xy - y x-y x y...

  • x^2+6x+8 - разложить многочлен на множители выделением полного квадрата двучлена и использованием формулы разности квадратов.


    Решение: X^2+6x+8 это не разложение квадрата суммы. так как вместо 8 должно стоять 9. чтобы добавить до полного квадрата двучлена надо прибавит 1. а чтобы наши действия были законными сразу же вычтем 1. (x^2+6x+8+1)-1=(x^2+6x+9)-1=
    (x+3)^2-1 это мы выделили полный квадрат двучлена, теперь применим формулу разности квадратов (x+3)-первое число, 1-второе число, единица в любой степени всегда=1. Получаем (x+3)^2-1^2=((x+3)-1)*((x+3)+1)=(x+3-1)*(x+3+1)=(x+2)*(x+4). Вот и все! Если хочете можно проверить-перемножить скобки-получится исходный квадратный трехчлен

<< < 91011 12 13 > >>