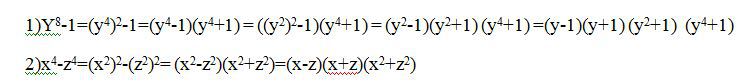многочлен »

разложить многочлен на множители - страница 10

  • Разложить многочлен на множители: а) х^4 – 6х^ 3 + 13х ^2 - 12х + 4
    б) х (y + z)^ 2 + y (z + x) ^2 +z (x+y)^ 2 - 4 x y z


    Решение: Разложить многочлены на множители:
     а) х^4 – 6х^ 3 + 13х ^2 - 12х + 4
    х=1 1^4 – 6(1^ 3 )+ 13(1 ^2) - 12(1) + 4 =1-6+13-12+4=0 ⇒
     х^4 – 6х^ 3 + 13х ^2 - 12х + 4=(х-1)(х^ 3 - 5х ^2 + 8х - 4)
    х=1 1^ 3 - 5(1 ^2) + 8(1) - 4=1-5+8-4=0 ⇒
    х^4–6х^3+13х^2-12х+4=(х-1)(х^3-5х^2+8х-4)=(х-1)(х-1)(х^2-4х+4)=(х-1)²(х-2)² ⇔
    х^4–6х^3+13х^2-12х+4=(х-1)²(х-2)²
    б) х (y + z)^ 2 + y (z + x) ^2 +z (x+y)^ 2 - 4 x y z

  • Разложить многочлен на множители в) у8-1 г) х4-z4


    Решение: Разность квадратов

    1)Y8-1=(y4)2-1=(y4-1)(y4+1) = ((y2)2-1)(y4+1) = (y2-1)(y2+1) (y4+1) =(y-1)(y+1) (y2+1) (y4+1)

    2)x4-z4=(x2)2-(z2)2= (x2-z2)(x2+z2)=(x-z)(x+z)(x2+z2)

    на скриншоте лучше показано

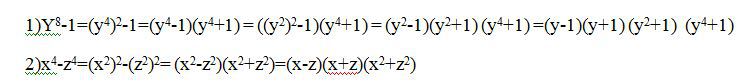
    Разность квадратов Y - y - y - y y - y y - y y y- y y y x -z x - z x -z x z x-z x z x z на скриншоте лучше показано...

  • Разложить множители на многочлен 3х4 + 6х3у + 3х2у2


    Решение: Вынесем 3*х*х=3x^2, получим:

    3x^2*(x^2+2ху+у^2)=(3x^2)*(х-у)*(х-у)=3*х*х*(х-у)*(х-у)

    x^2+2ху+у^2 - квадратное уравнение. можно решать через дискриминант, а можно по теореме Виетта: корни равны - х1=х2=у,

    поэтому данное уравнение можно разложить как (х-у)(х-у)

    ответ:3*х*х*(х-у)*(х-у)

    Разложить множители на многочлен 3х4 + 6х3у + 3х2у2

    3х4 + 6х3у + 3х2у2=3x^2(x^2+2xy+y^2)=3x^2(x+y)^2

    ^ это степень

  • Разложить многочлен на множители и решить уравнение У³-6+11у-6у²=0


    Решение: У³-6+11у-6у²=0
      у³-6у²+11у-6=0
      у³-6у²+11у+у-у-6=0
      у³-6у²+12у-у-6=0
      у³-у-(6у²-12у+6)=0
      у(у²-1)-6(у²-2у+1)=0
    решим уравнение у²-2у+1=0 у первое второе =1+/-√1-1 упервое=у второе=1 тогда получим такую запись 
      у(у²-1)-6(у-1)(у-1)=0 или у(у-1)(у+1)-6(у-1)(у-1)=0
      (у-1)< у(у+1)-6(у-1)>=0 (у-1)(у²+у-6у+6)=0 (у-1)(у²-5у+6)=0
      у-1=0 у=1 у²-5у+6=0 решим уравнение у первое второе =5/2+/-√25/4-6=5/2+/-1/2 упервое =3 у второе =2 можем записать (у-1)(у-3)(у-2)

  • Разложить многочлен на множители (X^7+x)-(x^7+y)
    x^4+4y^4


    Решение: Разложить многочлен на множители (X^7+x)-(x^7+y) и x^4+4y^4
    ========================
    (X^7+x)-(x^7+y) думаю неправильно
    (x⁷ +x) -(y⁷+y) =(x⁷-y⁷) +(x-y) =(x-y)(x⁶+x⁵y+x⁴y²+x³y³+x² y⁴+xy⁵+y⁶) +(x-y) =
    (x-y)(x⁶+x⁵y+x⁴y²+x³y³+x² y⁴+xy⁵+y⁶ +1).
    -
    x^4+4y^4 * * * x⁴+4y⁴ * * *
    x⁴+4y⁴ =(x²)² +(2y²)² =(x²)² +2*(x²)*(2y²) +(2y²)²  -2*(x²)*(2y²) =
    (x² +2y²)² -(2xy)² =(x² +2y² -2xy)(x² +2y² +2xy).

<< < 8910 11 12 > >>