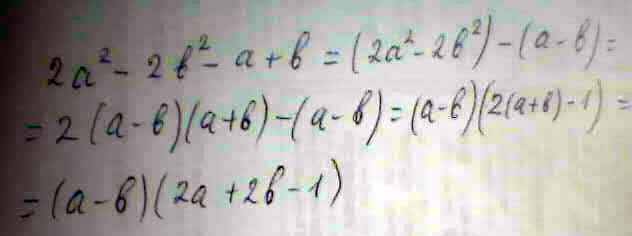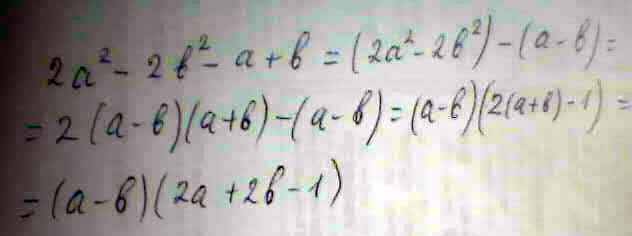разложить многочлен на множители - страница 9

1. разложите на множители
1) с в 3степени минус 36с
2)3а во в торой степени минус 18аб плюс 27 б во торой степени
номер 2
упростите
(3z-2)(2z+4)-(2z-1) во второй степени -9z
номер 3
преобразует в многочлен
1). (p-3)(p+4)-4p(2-p)
2). (y-6) во второй степени - 4 y(y+2)
3). 4(p-3) во второй степени
-4х во второй степени

1) с^3 - 36 c = c(c^2 - 36) = c(c-6)(c+6);
2) 3a^2 - 18 ab + 27 b^2= 3(a^2 - 6ab + 9 b^2) = 3(a - 3b)^2;
(3z -2)(2z+4) - (2z - 1)^2 - 9z= 6z^2 - 4z +12z -8 - (4z^2- 4z +1) - 9z =
= 6z^2 + 8z -8 - 4z^2+4z -1 - 9z= 2z^2 +12z -9.
3.1)(p-3)(p+4)-4p(2-p)= p^2 - 3p +4p - 12- 8p + 4 p^2=
=5p^2 -7p - 12.
2) (y-6)^2 - 4y(y+2)=y^2 - 12y + 36 - 4y^2 - 8y = - 3y^2 - 20y +36.
3) 4(p-3)^2 - 4p^2=4(p^2 - 12p + 9) - 4p^2= 4 p^2 - 48 p + 36 - 4p^2=
=- 48 p + 36.

Разложить многочлен на множители
5x^2-3x-2

5x^2-3x-2
a=5 b=-3 c=-2
D=b^2-4*ac=9-4*(-2)5=49=7^2
x1 = -b + корень из D/2a = 3+7/10 = 1
x2 = -b - корень из D/2a = 3-7/10 = - 0,4

Разложить многочлен на множители 2a^4 - a^2 - 1

-

2а⁴-a²-1=2а⁴+(2а³-2а³)+(-2а²+а²)+(а-а)-1=(2а⁴-2а³)+(2а³-2а²)+(а²-а)+(а-1)=

2а³(а-1)+2а²(а-1)+а(а-1)+(а-1)=(а-1)(2а³+2а²+а+1)

разложить многочлен на множители х^3 - 7х + 6

-

х³-7х+6=х³+(-х²+x²)+(-6х-х)+6=х³-х²+x²-6х-х+6=(х³-х²)+(x²-х)+(-6х+6)=(х³-х²)+(x²-х)-(6х-6)=х²(х-1)+х(х-1)-6(х-1)=(х-1)(х²+х-6)

разложить многочлен на множители
2a^2-2b^2-a+b
^ степень

2a^2-2b^2-a+b= 2(a^2-b^2)-a+b=(формула разности квадратов)=2(a-b)(a+b)-a+b=
=2(a-b)(a+b)-(a-b)=(a-b)(2(a+b)-1)=2(a-b)(a+b-1/2)