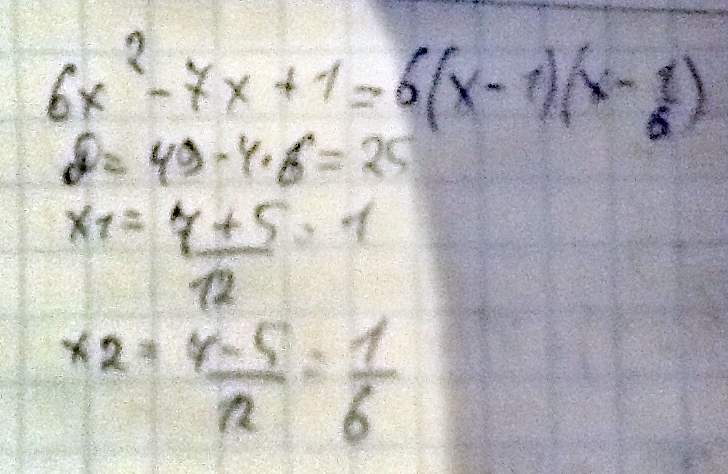многочлен »
разложить многочлен на множители - страница 14
Разложите на множители многочлен 6x^2-7x+1
Решение: 6x^2-7x+1=0
7+-√49-24
х=-12
7+-5
х=-12
х=1
х=1/6
6x^2-7x+1=6 (х-1/6) (х-1)= (6х-1) (х-1)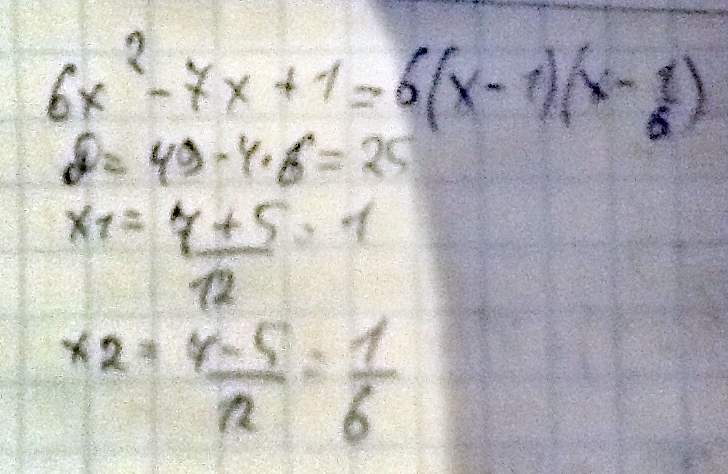
Разложите на множители многочлен м^2 - у^2+10у-25
Решение: $$ m^2 - y^2+10y-25=m^2-(y-5)^2=(m-y+5)(m+y-5) $$Разложите на множители многочлен, если возможно. 6х в квадрате+9х-10
Решение: Для того чтобы разложить данный многочлен на множители, приравняем его к нулю. В результате получится квадратное уравнение.
6x²+9x-10=0
Находим дискрименант:
D=b²-4ac=9²-4*6*(-10)=81+240=321
Т. к. число 321 не является квадратом целого числа, то разложить данный многочлен на множители нельзя.
Разложите множители на многочлен
1.
1) 9a^2-9
2) 2m-2m^3
3) x^2-x^4
4) y^3-y^5
5) mx^2-my^2
2.
1) -4x+4+x^2
2) 2m^2-4m+2
3) 6x^2+24y^2+24xy
4) 36+24x+4x^2
3.
1) x^6 - 1
2) 2x^3 - 16
4.
1) 60+6ab-3ab-12a
2) ac^4-c+ac^3-c^3
3) -5xy-40y-15x-120
4) x^3-x^2 y+x^2-xy
5.
1) a^2-b^2-a+b
2) 4m^2-2n+4m-n^2
3) x^2-y^2-x-y
4) m-d+m^2-d
5) c^2+d-d^2+c
Решение: N4 1)=c³(ac+a-1) 3)=-((5xy+15x)-(40y+120)= -5x(y+3)-40(y+3)= (y+3)(-5x-40)=-5(y+3)(x+8) 4)= (x³-x²y)+(x²-xy)= x²(x-y)+x(x-y)= (x-y)(x²+x)= x(x-y)(x+1)
N51)= (a²-b²)-(a-b)= (a-b)(a+b)-(a-b)= (a-b)(a+b-1) 2)=(4m²-n²)+(4m-2n)=
=(2m-n)(2m+n)+2(2m-n)=(2m-n)(2m+n+2)
3)=(x²-y²)-(x+y)=(x-y)(x+y)-(x-y)= (x-y)(x+y-1)
5)=(с²-d²)+(c+d)=(c+d)(c-d)+(c+d)=(c+d)(c-d+1)
N1) 1)=9(a²-1)=9(a-1)(a+1) 2)=2m(1-m²)=2m(1-m)(1+m) 3)=x²(1-x²)=x²(1-x)(1+x)
4)= y³(1-y²)=y³(1-y)(1+y) 5)m(x²-y²)=m(x+y)(x-y)
N2) 1)=(x²-1)(x^4+x²+1)=(x-1)(x+1)(x^4+x²+1) 2)=2(x³-8)=2(x-2)(x²+2x+4)Разложите на множители многочлен 9a²b-3a²+3b²-b
Решение: Здесь легче разложить с помощью метода групп:
Мы найдем общее между $$ 9a^2b-3a^2 $$ и $$ +3b^2-b $$
Первая группа делится и на \(a^2 \) и на 3, получаем:
$$ 3a^2(3b-1) $$
Вторая делится на b:
$$ b(3b-1) $$
Как можно заметить, мы получили следующее:
$$ 3a^2(3b-1)+b(3b-1) $$ - выражение 3b-1 у обоих групп, поэтому можно разложить еще:
$$ (3a^2+b)(3b-1) $$ И это будет окончательный ответ.