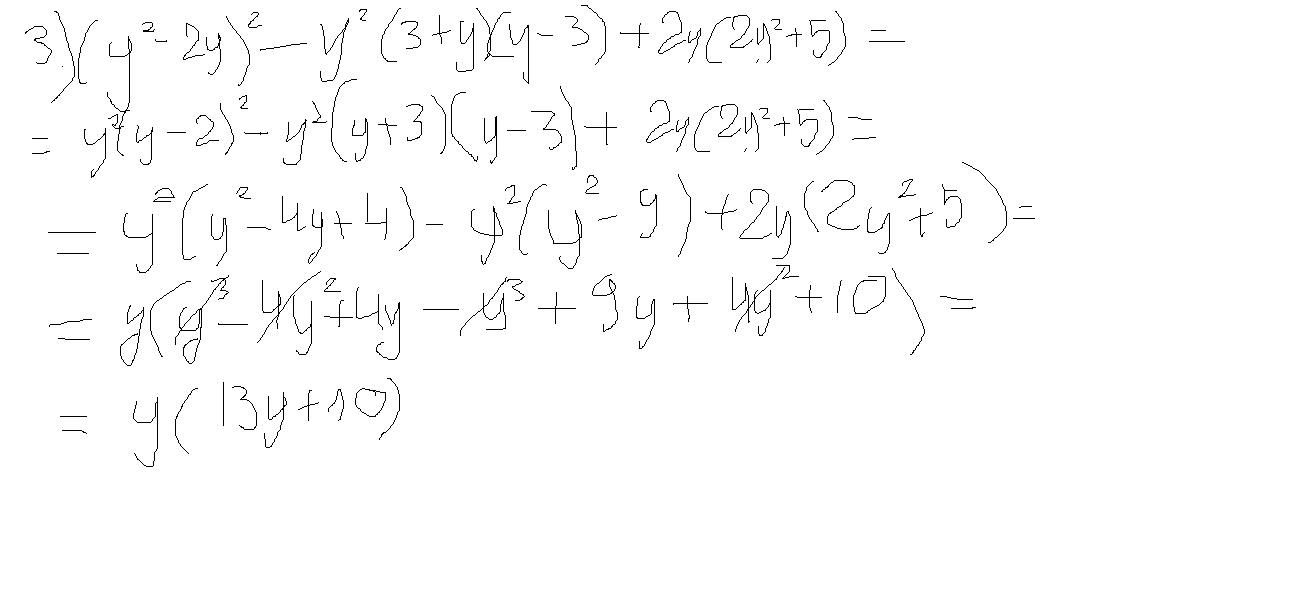многочлен »

разложите многочлен на множители - страница 3

  • Разложите многочлен на множители: 3y2-12y ab-2a+b2-2b 4x2-9 x3-8x2+16x 6n3+6m3 16m4-81n4 (3y2 - 3y во 2 степени, b2 - b во 2 степени и тд) Решите уравнение (x-4)2-25=0 ((x-4)2 это (x-4) во второй степени)


    Решение:

    3y^2-12y=3y(y-4)

    ab-2a+b^2-2b=a(b-2)+b(b-2)=(b-2)(a+b)

    4x^2-9=(2x-3)(2x+3)

    x^3-8x^2+16x=x(x^2-8x+16)=x(x-4)^2

    6n^3+6m^3=6(n^3+m^3)=6(n+m)(n^2+mn+m^2)

    16m^4-81n^4=(4m^2-9n^2)(4m^2+9n^2)=(2m-3n)(2m+3n)(4m^2+9n^2)

    (x-4)^2-25=0

    (x-4-5)(x-4+5)=0

    (x-9)(x+1)=0

    x=9

    x=-1

    $$ 3y^2-12y=3y(y-4)\ \\ ab-2a+b^2-2b=(ab-2a)+(b^2-2b)=a(b-2)+b(b-2)=\\ =(b-2)(a+b) \\ 4x^2-9=(2x-3)(2x+3) \\ x^3-8x^2+16x=x(x^2-8x+16)=x(x-4)^2 \\ 6n^3+6m^3=6(n^3+m^3)=6(n+m)(n^2-mn+m^2) \\ 16m^4-81n^4=4^2(m^2)^2-9^2(n^2)^2=(4m^2-9n^2)(4m^2+9n^2)=\\ =(2m+3n)(2m-3n)(4m^2+9n^2) \\ (x-4)^2-25=0\\ x^2-8x+16-25=0\\ x^2-8x-9=0\\ D=(-8)^2-4*1*(-9)=64+36=100\\ x_1=\frac{8+10}{2}=9\\ x_2=\frac{8-10}{2}=-1 $$

    Ответ: 9 и -1

  • разложите многочлен на множители комбинируя различные способы: 16-m в 2 степени+2mn-n в 2 степени а в 3 степени + аb в 2 степени + а в 2степени b + b в 3 степени m в 3 степени + 10 m +5 m в 2 степени + 8


    Решение: Если это три разных многочлена, то :

    1) 16m^2+2mn - n^2=(16m^2 - n^2)+2mn=(4m - n)(4m+n)+2mn

    2) а^3+ab^2+a^2b b^3 = ( а^3 + b^3 )+(ab^2+a^2b ) = (a+b)(a^2 - ab+b^2)+ab(b+a) =
    =(a+b)(a^2 - ab+b^2+ab)=(a+b)( a^2+b^2)

    3) m^3+10m+5m^2+8= (m^3 +8) +(10m+5m^2)=(m+2)(m^2 - 2m+4)+5m(2+m)=
    =(m+2)(m^2 - 2m+4+5m)=(m+2)(m^2 +3m+4) 

    $$ 1)\ 16-m^2+2mn-n^2=16-(m^2-2mn+n^2)= \\ \ =4^2-(m-n)^2=(4+m-n)(4-m+n) \\ \ 2)\ a^3+ab^2+a^2b+b^3=a^3+a^2b+ab^2+b^3= \\ =a^2(a+b)+b^2(a+b)=(a+b)(a^2+b^2) \\ \ 3)\ m^3+10m+5m^2+8=(m+2)(m^2-2m+4)+5m(2+m)= \\ =(m+2)(m^2-2m+4+5m)= (m+2)(m^2+3m+4) $$

  • Представьте данный многочлен в виде квадрата двучлена: m в 2 степени + 2mn + n в 2 степени= 4а в 2 степени-4аb в 2 степени + b в 2степени= 100р в 2 степени - 60р + 9= 49х в 2 степени у в 2 степени - 14ху + 1= t в 4 степени - 26t в 2 степени + 169= разложите многочлен на множители используя соответствующую формулу сокращения уножения, / - вот этот знак значит дробй : 9х в 2 степени - у в 2 степени= 16 с в 2 степени d в 2 степени - 25t в 2 степени= х в 4 степени/81 - 49у в 2 степени/36 = 8t в 3 степени + 27р в 12 степени= х в 3 степени - 1000= у в 6 степени/125 + 0,064=


    Решение: 1. (m+n)(m+n)

    2. наверное ошибка, 4 ав должно быть просто, без степени. сделала без степени (2а-в)(2а-в)

    3. (10р-3)(10р-3)

    4. (7ху-1)(7ху-1)

    5. (t^2-13)(t^2-13)

    6. (3x-y)(3x+y)

    7. (4cd-5t)(4cd+5t)
    8. (x^2/9- 7y/6)(x^2/9+ 7y/6)

    9. (2t+3p^4)(9p^8-6p^4*t+4t^2)

    10. (x-10)(x^2+10x+100)

    11 не знаю

    $$ 1) m^{2}+2mn+n^{2}=(m+n)^{2} $$

    $$ 2) 4a^{2}-4ab+b^{2}=(2a-b)^{2} $$

    $$ 3) 100p^{2}-60p+9=(10p-3)^{2} $$

    $$ 4)49x^{2}y^{2}-14xy+1=(17xy+1)^{2} $$

    $$ 5)t^{4}-26t^{2}+169=(t^{2}-13)^{2} $$

    $$ 6)9x^{2}-y^{2}=(3x-y)(3x+y) $$

    $$ 7)16c^{2}d^{2}-25t^{2}=(4cd-5t)(4cd+5t) $$

    $$ 8)\frac{x^{4}}{81}-\frac{49y^{2}}{36}=(\frac{x^{2}}{9}-\frac{7y^{2}}{6})(\frac{x^{2}}{9}+\frac{7y^{2}}{6}) $$

  • 1. Представьте выражение в виде многочлена: а)(4x+3)(4x-3)
    б)(3x-2)^2
    в)(x+5)(x^2-5x+25)
    2.Разложите многочлен на множители:
    а)x^3-9x
    б)-5a^2-10ab-5b^2
    в)25x^2-y^2
    3.Упростите выражение:
    (y^2-2y)^2-y^2(3+y)(y-3)+2y(2y^2+5)
    4.Докажите, что выражение x^2-4x+9 может принимать лишь положительные значения.
    с полными ответами, ^2 и ^3 значит во второй степени и в третьей.


    Решение: Формулы сокращенного умножения, здесь даже объяснять нечего

    1) 16х2-9

    2) 9х2-2*3х*2+4=9х2-12х+4

    3)х3+125

    2.1

    выносим х за скобки: х(х2-9)<---формула= х(х2-6х+9)

     2.2

    выносим -5 за скобки: -5(а2+2аб+б2)<----формула= -5(а+б)^2

    2.3

    формула тут

    (5х-у)(5х+у)

    Формулы сокращенного умножения здесь даже объяснять нечего х - х - х х - х х . выносим х за скобки х х -...

  • Разложите на множители: 64m^3-1 Разложите многочлен на множители: k^6-(pq)^6 Решите уравнение: (x-3)(x^2+3x+9)-x(x^2-16)=21 Упростите выражение: (a+3)^3-(a-1)^3-12a^3 Решите уравнение: (x+2)^3-x(3x+1)^2+(2x+1)(4x^2-2x+1)=42 Выполните действие: (x^n+x^n-1)^3 Докажите справедливость равенства(Тождества): (a-1)^3+3(a-1)^2+3(a-1)+1+a^3


    Решение: 1)       64m^3 -1 = (4m)^3 - 1^3  =  (4m - 1)*(16m^2 + 4m + 1)

    2)       (x-3)*(x^2 +3x +9) - x(x^2 -16) = 21

               x^3  -  3^3  -  x^3  +  16x^2  =  21

               16x^2   =  21  +  27

                16x^2  =  48

                 x^2   =   3

                  x_1    =   -V3,           x_2    =    V3

    3)     (a+3)^3 - (a-1)^3 - 12a^3  =  a^3  +  3a^2*3  +  3a*9  +  27  -  a^3  + 3a^2 * 1  -  3a*1  +  1  -

                   -12a^3  =  -12a^3  +  12a^2  + 24a  +  28  =  -4(a^3  -  3a^2  -  6a  -  7)

    4)           (x+2)^3  -  x(3x+1)^2  +   (2x+1)(4x^2 -2x+1)   =  42

                    x^3  +  3x^2 *2  +  3x*2^2  +  2^3  -  9x^3  -  6x^2  -  x  +  (2x)^3  +  1^3  -42  =  0

                    11x  =  33

                      x   =  3

    5)           (x^n  +  x^(n-1))^3  =  x^3n  +  3x^2n *x^(n-1)  +  3x^n *(x^(n-1))^2  +  (x^(n-1))^3  =

                   =    x^3n  +  3x^(3n-1)  +  3x^(3n -2)  +  x^(3n-3)  =  x^3n(1  +  3x^(-1)  +  3x^(-2)  + x^(-3))

    6)         (a-1)^3  +  3(a-1)^2  +  3(a-1)  +  1  +  a^3  =  a^3  -  3(a-1)^2  +  3(a-1)  -  1  +3(a-1)^2  +

                 +3(a-1)  +  1+  a^3  =  2a^3  +  6(a-1)  +  1  =  2a^3  +  6a  -  5

<< < 123 4 5 > >>