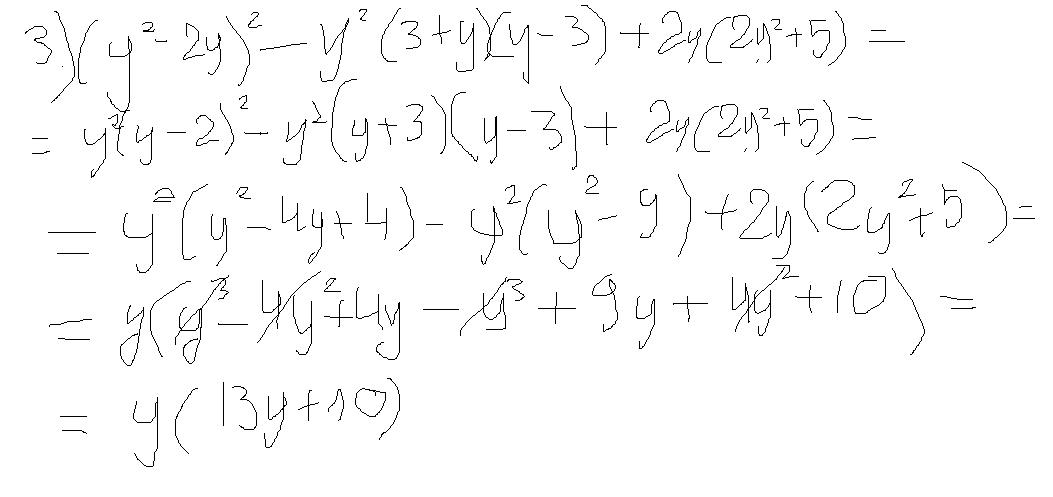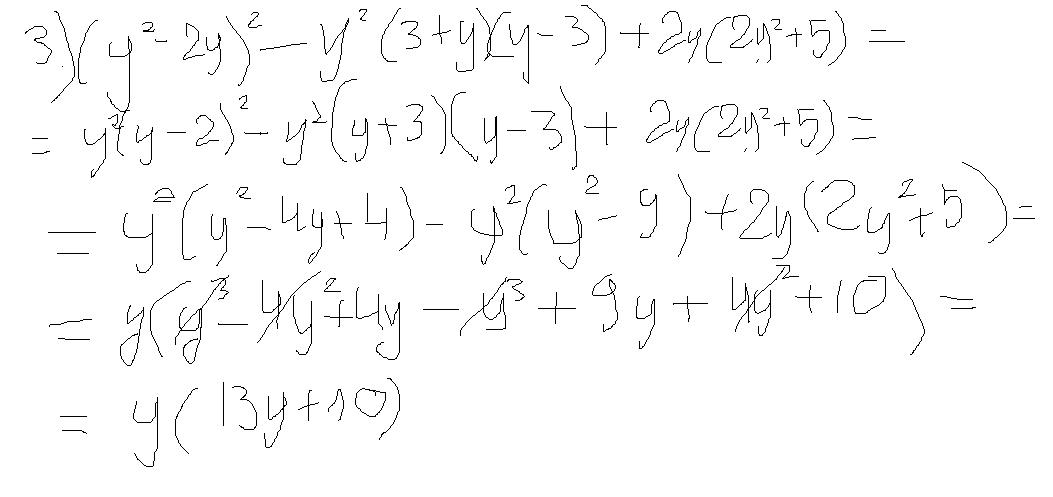разложите многочлен на множители - страница 4
Разложите многочлен на множители представив один из его членов в виде суммы подобных слагаемых:
а^2 - 7а +6
Решение: Такой метод ещё называется группировкой.
Особо его не объясните, нужно просто решать самой(му) подобные примеры, и ты научитеся это видеть. Смотри, как это работает на примере.
$$ a^2-7a+6 = a^2 - a - 6a+6 = (a^2 - a) + (- 6a+6) = \\ = a(a-1) -6 (a-1) = (a-1)(a-6). $$
Замечу, что можно было найти корни этого уравнения, они равны 1 и 6, и записать точно такое же разложение. Способов много, ответ один.1. разложите многочлен на множители.
а. 3х(в квадр.)-12х
б. ав-2а+в(в квадр.)-2в
в. 4х(в квадр.)-9
г. х(в кубе)-8х(в квадр )+16х
2. вычислите наиболее рациональным способом
а. 87*43+(87 (в кубе )-43(в кубе) : 44 )
б.(169(в кубе)+59(в кубе) : 228)-169 *59
3. решите уравнение
х(в кубе )-64х=0
Решение: $$ 1) a) 3x^2 - 12x = 3x(x-4)\\\\ b) ab - 2a + b^2 - 2b = a(b-2) + b(b-2) = (a+b)(b-2)\\\\ c) 4x^2-9 = (2x -3)(2x+3)\\\\ d) x^3-8x^2+16x = x(x^2-8x+16) = x(x-4)^2\\\\ 2. a) 87*43+((87^3-43^3)/44) =\\ 87*43+ (87-43)(87^2+43*87 +43^2)/44 =\\ 87*43 + 87^2+43*87 +43^2 = \ \\ 87^2+2*43*87 +43^2 =\\ (87+43)^2 = 130^2 = 16900\\\\ b) ((169^3+59^3) : 228)-169 *59 =\\ (169+59)(169^2-169*59+59^2):228 - 169*59 =\\169^2-2*169*59+59^2 =\\ (169-59)^2 = 110^2 = 12100\\\\ 3. x^3 - 64x = 0\\\\ x(x^2-64) = 0\\\\ x^2-64 = 0, x_1 = 8, x_2 = -8\\ x = 0, x_3 = 0 $$1) а) 3х^2-12x=3x(x-4)=0 следовательно 3x=0; x=0. x-4=0; x=4
б) (ab-2a)+(b^2-2b); a(b-2)+b(2-b) ; (b-2)(a-b)
в) (2x-3)(2x+3)=0; x=3/2; x=-3/2
3) x^3-64x=0; x(x^2-64)=0; x(x-8)(x+8)=0; x1=0; x2=8; x3=-8
Решите уравнение: 36a^2 - 25 = 0
Разложите многочлен на множители: 512b^3 - 125; 216x^3 - y^3;
Представьте выражение в виде квадрата двучлена: 1 - 2b + b^2; x^2 - 14xy + 49y^2; 4m^2 - 28mn + 49n^2;
Разложите многочлен на множители: 625 - (n + 12)^2; (m + 10)^2 - (n - 12)^2
Решение: $$ 30.9 \ 36a^2 - 25 = 0\\\\ (6a)^2 - 5^2 = (6a - 5)(6a + 5) = 0\\\\ 6a \mp 5 = 0, \ 6a = \pm 5, \ \boxed{a = \pm\frac{5}{6}}\\\\ 30.12 \ 512b^3 - 125 = (8b)^3 - 5^3 = \boxed{(8b - 5)(64b^2 + 40b + 25)}\\\\ 30.14 \ 216x^3 - y^3 = (6x)^3 - y^3 = \boxed{(6x - y)(36x^2 + 6xy + y^2)}\\\\ \\ 30.16 \ 1 - 2b + b^2 = 1 - b - b + b^2 =\\\\ = (1- b) - b(1 - b) = (1-b)(1-b) = \boxed{(1 - b)^2}\\\\ 30.18 \ x^2 - 14xy + 49y^2 = x^2 - 7xy - 7xy + 49y^2 = \\\\ = x(x - 7y) - 7y(x - 7y) = (x - 7y)(x- 7y) = \boxed{(x - 7y)^2}\\\\ 30.19 \ 4m^2 - 28mn + 49n^2 = 4m^2 - 14mn - 14mn + 49n^2 = \\\\ = 2m(2m - 7n) - 7n(2m - 7n) = (2m - 7n)(2m - 7n) = \boxed{(2m - 7n)^2}\\\\ \\ 30.21 \ 625 - (n + 12)^2 = 25^2 - (n + 12)^2 = \\\\ = (25 - n - 12)(25 + n + 12) = \boxed{(13 - n)(37 + n)}\\\\ 30.23 \ (m + 10)^2 - (n - 12)^2 = (m + 10 - n + 12)(m + 10 + n - 12) = \\\\ = \boxed{(m - n + 22)(m + n - 2)} $$
16.3 вычислите наиболее рациональным способом:
1. 22 в 2 степени +2*22*38+38 в 2 степени
2. 103 в 2 степени - 2*103*3 + 3 в 2 степени
3. з9 в 2 степени-19 в 2 степени
4. 63,5 в 2 степени -13,5 в 2 степени
16.4 Решите уравнения:
х в 2 степени - 144=0
х в 2 степени+2ох+100=0
х в 2 степени -30 х+225=0
хв 5 степени - 81х=0
15.3 Разложите многочлен на множители способом группировки:
ав+3а+2в+6=
24м в 2 степени+6мр-4мn-np=
15.6 разложите многочлен на множители:
5а-ав в 2 степени -а в 2 степени в -5 в=
Решение: 1. 22² +2*22*38+38²=(22+38)²=60²=36002. 103² - 2*103*3 + 3²=(103-3)²=100²=10000
3. 39²-19²=(39-19)(39+19)=20*58=1160
4. 63,5² -13,5²=(63,5-13,5)(63,5+13,5)=50*77=3850
16.4Решите уровнения:
х² - 144=0
(х-12)(х+12)=0
х-12=0 или х+12=0
х=12 х=-12
х²+20х+100=0
(х+10)²=0
х+10=0
х=-10
х² -30 х+225=0
(х-15)²=0
х-15=0
х=15
х⁵ - 81х=0
х(х⁴-81)=0
х(х²-9)(х²+9)=0
х(х-3)(х+3)(х²+9)=0
х=0 или х-3=0 или х+3=0
х=3 х=-3
Ответ: 0; 3; -3
15.3 Разложите многочлен на множители способом группировки:
ав+3а+2в+6=а(в+3)+2(в+3)=(в+3)(а+2)
24м²+6мр-4мn-np=6м(4м+р)-n(4м+р)=(4м+р)(6м-n)
15.6 разложите многочлен на множители:
5а-ав² -а²в +5 в=5(a+b)-ab(a+b)=(a+b)(5-ab)
1. Представьте выражение в виде многочлена:
а)(4x+3)(4x-3)
б)(3x-2)^2
в)(x+5)(x^2-5x+25)
2. Разложите многочлен на множители:
а)x^3-9x
б)-5a^2-10ab-5b^2
в)25x^2-y^2
3. Упростите выражение:
(y^2-2y)^2-y^2(3+y)(y-3)+2y(2y^2+5)
4. Докажите, что выражение x^2-4x+9 может принимать лишь положительные значения.
Решение: Формулы сокращенного умножения, объяснять нечего1) 16х2-9
2) 9х2-2*3х*2+4=9х2-12х+4
3) х3+125
2.1
выносим х за скобки: х(х2-9)<-формула= х(х2-6х+9)
2.2
выносим -5 за скобки: -5(а2+2аб+б2)<-формула= -5(а+б)^2
2.3
формула тут
(5х-у)(5х+у)