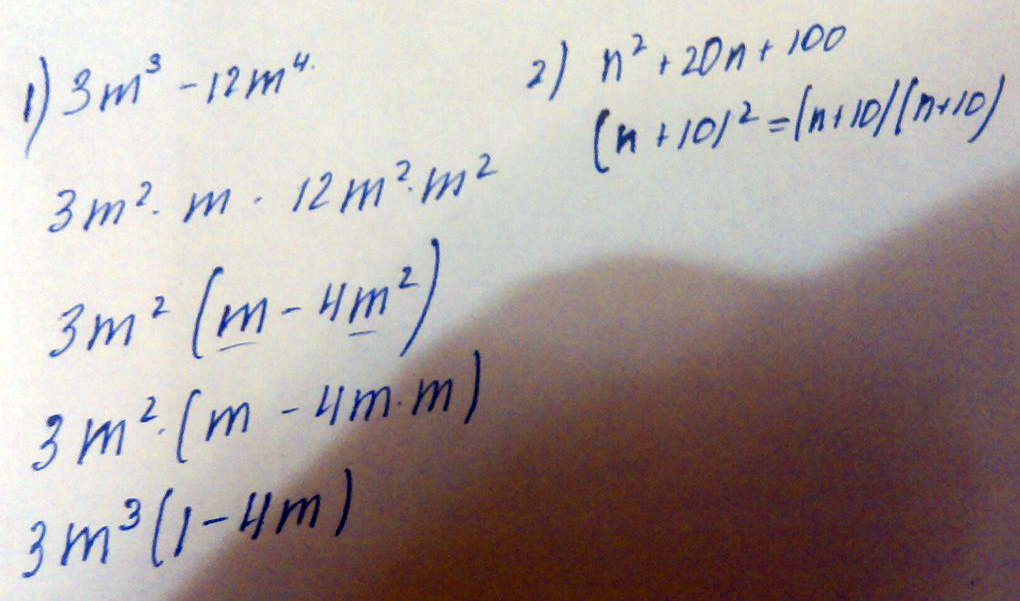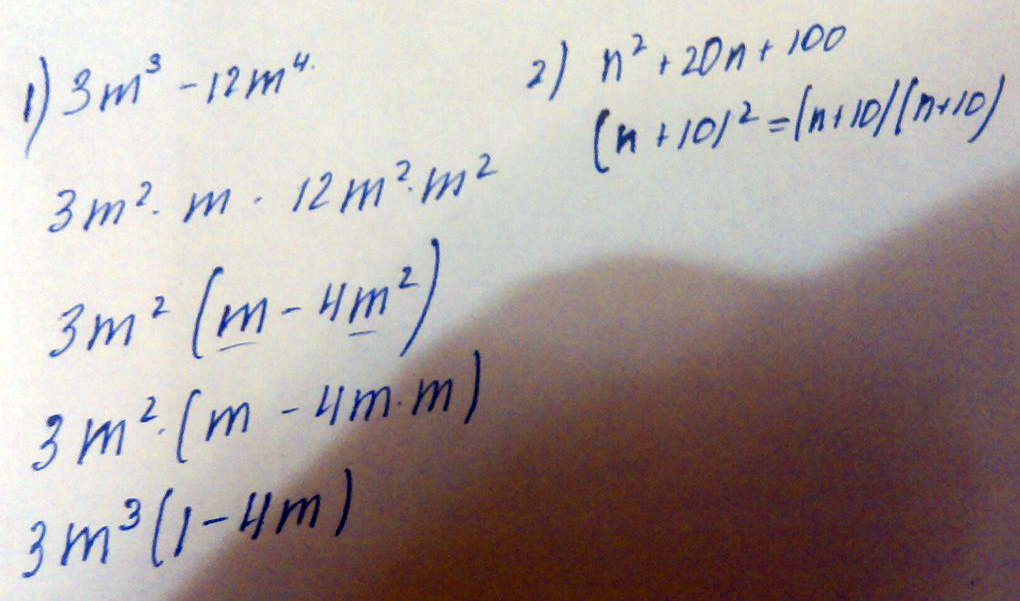разложите многочлен на множители - страница 6
Разложите многочлен на множители:
3y2-12y
ab-2a+b2-2b
4x2-9
x3-8x2+16x
6n3+6m3
16m4-81n4
(3y2 - 3y во 2 степени, b2 - b во 2 степени и тд)
Решите уравнение
(x-4)2-25=0
((x-4)2 это (x-4) во второй степени)
Решение: 3y^2-12y=3y(y-4)ab-2a+b^2-2b=a(b-2)+b(b-2)=(b-2)(a+b)
4x^2-9=(2x-3)(2x+3)
x^3-8x^2+16x=x(x^2-8x+16)=x(x-4)^2
6n^3+6m^3=6(n^3+m^3)=6(n+m)(n^2+mn+m^2)
16m^4-81n^4=(4m^2-9n^2)(4m^2+9n^2)=(2m-3n)(2m+3n)(4m^2+9n^2)
(x-4)^2-25=0
(x-4-5)(x-4+5)=0
(x-9)(x+1)=0
x=9
x=-1
$$ 3y^2-12y=3y(y-4)\\ \\ ab-2a+b^2-2b=(ab-2a)+(b^2-2b)=a(b-2)+b(b-2)=\\ =(b-2)(a+b)\\ \\ 4x^2-9=(2x-3)(2x+3)\\ \\ x^3-8x^2+16x=x(x^2-8x+16)=x(x-4)^2\\ \\ 6n^3+6m^3=6(n^3+m^3)=6(n+m)(n^2-mn+m^2)\\ \\ 16m^4-81n^4=4^2(m^2)^2-9^2(n^2)^2=(4m^2-9n^2)(4m^2+9n^2)=\\ =(2m+3n)(2m-3n)(4m^2+9n^2) \\ \\ \\ (x-4)^2-25=0\\ x^2-8x+16-25=0\\ x^2-8x-9=0\\ D=(-8)^2-4*1*(-9)=64+36=100\\ x_1=\frac{8+10}{2}=9\\ x_2=\frac{8-10}{2}=-1 $$
Ответ: 9 и -1
РАЗЛОЖИТЬ НА МНОЖИТЕЛИ МНОГОЧЛЕН 6x^3-25x^2+3x+4
Решение: разложим по схеме горнера:6x^3-25x^2+3x+4 нужно перебрать все числа, на которые делится число 4, это 1,1,2,2,4,4
нужно подставлять их вместо х и выбрать то число, при котором выражение равно 0!
в данном случае это число 4 (k=4)
6*64-25*16+12+4=384-400+12+4=0
теперь составляем таблицу:
6 -25 3 4 (- это коэф. 6x^3-25x^2+3x+4)
k=4(x-4) 6 4*6+(-25)=-1 -1*4+3=-1 -1*4+4=0
получим:(x-4)(6x^2-1x-1)
теперь осталось разложить 6x^2-1x-1 с помощью дискриминанта:
D=1+24=25;
x1=1+5/12=1/2; x2=1-5/12=-1/3
(x-4)(x-1/2)(x+1/3)
Разложить на множители многочлен:
1) 4x^4+4x^3-25x^2-x+6
2) x^4-2x^3-14x^2-6x+5
Решение: Решено методом подбора. При разложении полинома используем его свойство иметь целочисленные корни, являющиеся делителями свободного члена.

Разложить на множители многочлен \( 6x^3 - 25x^2 +3x +4 \).
Решение: 6х³ - 25х² + 3х + 4 = 6 (х - 4)(х - ½)(х + ⅓) = (х - 4) * 2(х - ½) * 3(х + ⅓) = (х - 4)(2х - 1)(3х + 1)Разложить на множители многочлен
1)3m^3-12m^4
2)n^2+20n+100
Решение: $$ 3 m^{3} - 12 m^{4}=3 m^{3}(1-4m) \\ n^{2}+20n+100=(n+10)(n+10)=(n+10)^2 $$Должно быть так, во втором можно в квадрате оставить, а можно разложить)