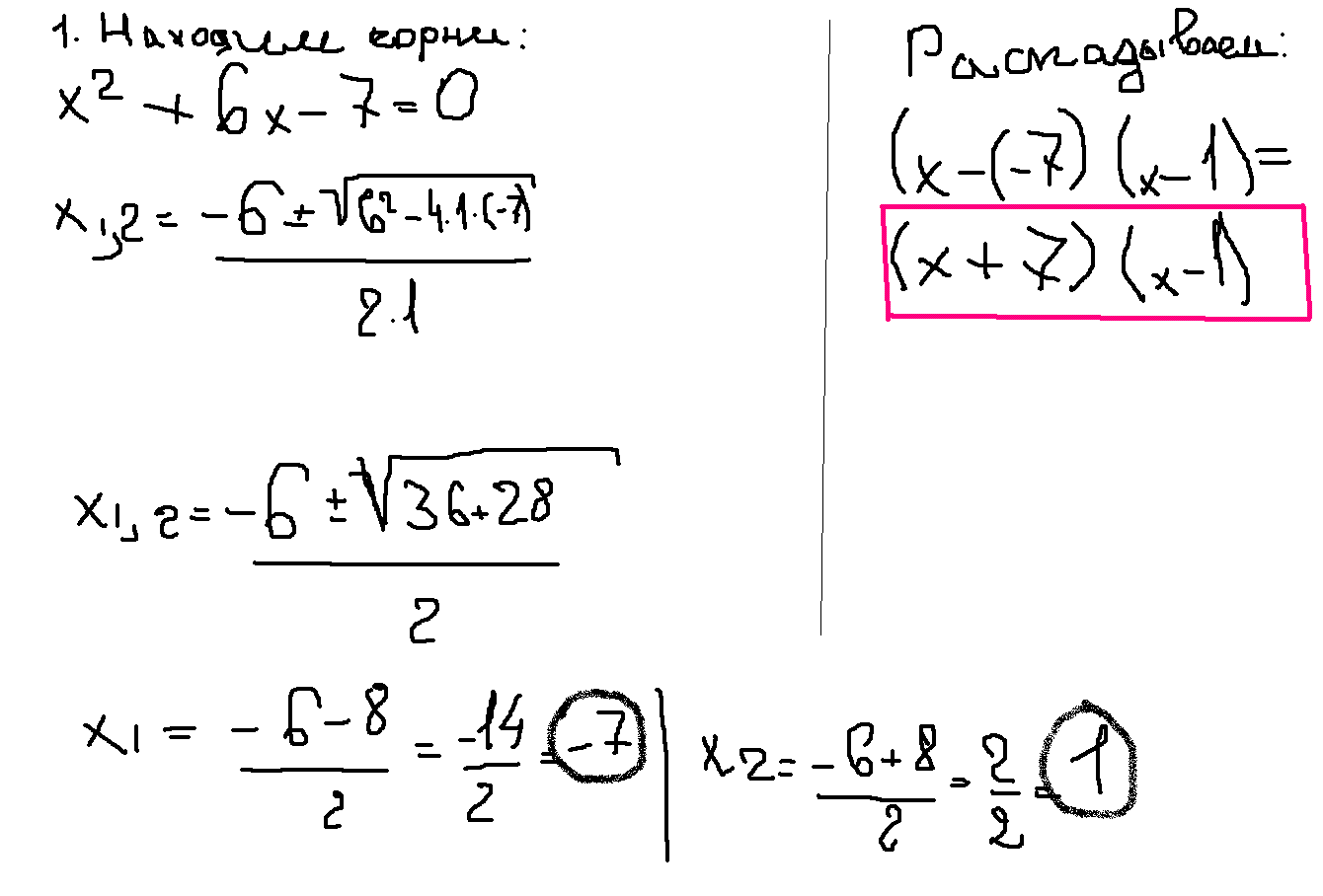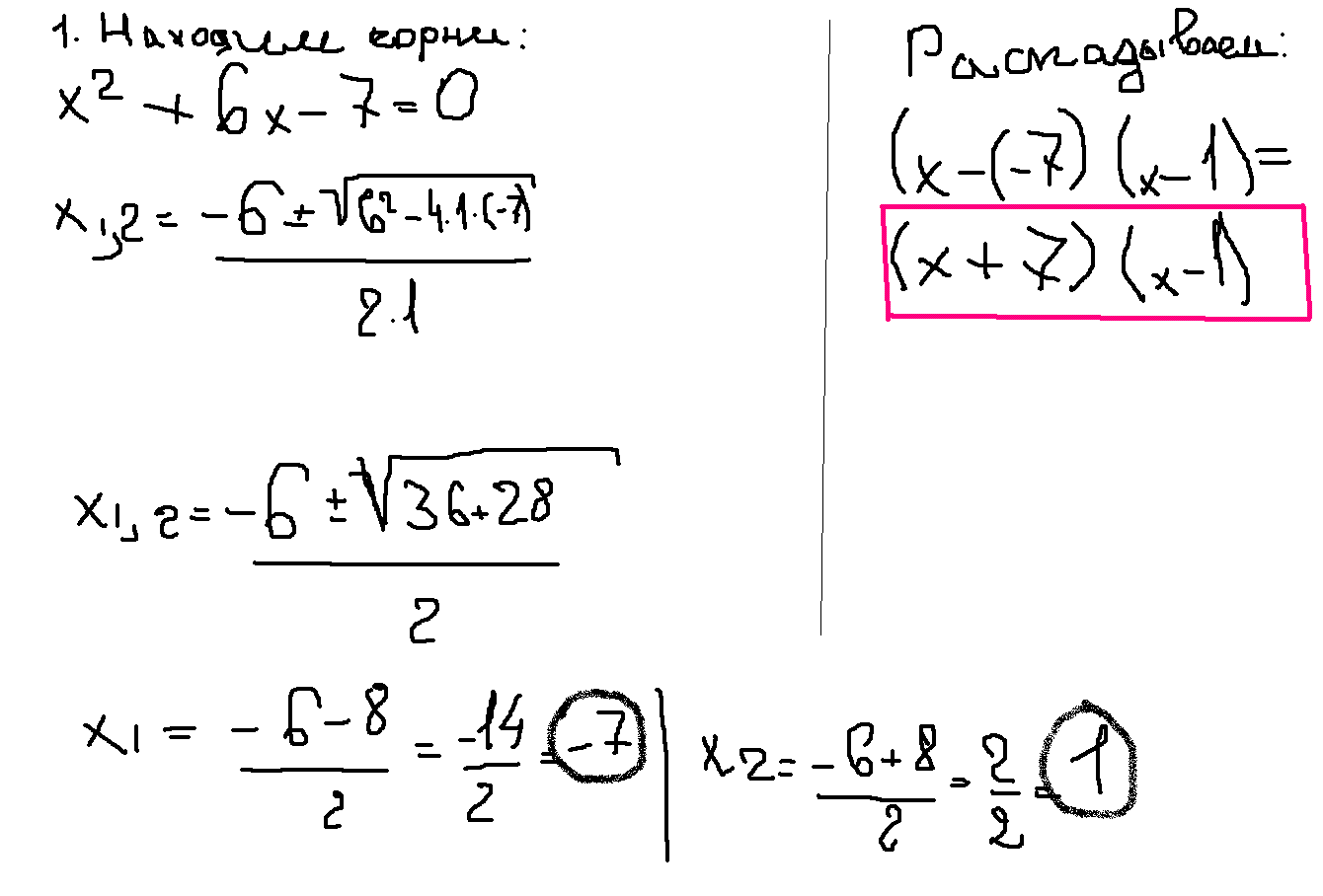многочлен »
разложите многочлен на множители - страница 7
Как разложить на множители многочлен 6x^ + 7x − 5.
Решение: Нужно найти дискриминант по формуле D=b²-4ac и найти корни по формуле x₁₂=(-b+(-)√D)/(2a). Дальше представить трехчлен в виде a(x-x₁)(x-x₂)
6x² + 7x − 5
D=49+4*5*6=169
x₁=(-7+13)/12=0,5
x₂=(-7-13)/12=-5/3
6x² + 7x − 5 = 6 (x - 0,5) (x + 5/3)= (2x-1) (3x+5)
6x²+7x-5= 6(x-1/2)(x+5/3) = (2x-1)(3x+5)
6x²+7x-=0
D= 49+4*6*5= 169
x₁= (-7+13)/12 = 6/12= 1/2,
x₂= (-7-13)/12 = -20/12 = -5/31. Разложить на множители многочлен:
а) 5x – 10xy; б) 3m3 – 12m4
; в) 0,25a
2 – b
6 г) n
2 + 20n + 100
2. Найти числовое значение выражения при заданном значении переменной, предварительно
упростив его:
14b + (b + 7)(b – 7) + (b – 7)
2
, при b =
3. Разложить на множители выражение и выяснить может ли его значение равняться нулю:
(a
2 + 2)(a – 1) – a·(a
2 + 2)
4. Разложить на множители:
а)
б) 3a(b – 4) – 2b + 8
в) x
3 + 3x
2 – x – 3
6. Вычислить:
а) 123
2 – 77
2
; б) ; в) ; г) (99
2 + 97
2 + 95
2 + 93
2
) – (98
2 + 96
2 + 94
2 + 92
2)
Решение: 1)
а)=5х(1-2у)
б)=3м^3(1-4м)
в)=(0.5а-б^3)(0.5а+б^3)
г)=(н+10)^2
2)
=14б+б^2-49+б^2-14б+49=
=б^2
подставите вместо "б" число
3)
=(а^2+2)(а-1-а)=-а^2-2
-а^2-2=0
-а^2=2
а^2=-2
не может
4)
б)=3а(б-4)-2(б-4)=(б-4)(3а-2)
в)=х^2(х+3)-(х+3)=(х+3)(х^2-1)=
=(х+3)(х-1)(х+1)
5)
б)
а^2-3а=2а-6
а^2-5а+6=0
д=25-4×6=1
а1=(5-1)/2=2
а2=(5+1)/2=3Решить разложить на множители многочлен \( 1) 2x^2 + x - 3x^3;\\ 2) y^3-3y^2+y;\\ 3) 3xy^2-x^2y+x^2y^2; \\4) m^3n^2+2m^2n^3-m^2n^2;\\ 5) 10a^4b + 15a^3b^2 -5ab^3;\\ 6) 6c^3d - 12c^2d^3 + 18c^3d^2\)
Решение: Вот и твоя задачка решена tj04$$ 2x^2+x-3x^3=x(2x+1-3x^2)=-x(3x^2-2x-1)=\\=-3x(x-1)(x+ \frac{1}{3} )\\\\y^3-2y^2+y=y(y^2-2y+1)=y(y-1)^2\\\\3xy^2-x^2y+x^2y^2=xy(3y-x+xy)\\\\m^3n^2+2m^2n^3-m^2n^2=m^2n^2(m+2n-1)\\\\10a^4b+15a^3b^2-5ab^3=5ab(2a^3+3a^2b-b^2)\\\\6c^3d-12c^2d^3+18c^3d^2=6c^2d(c-2d^2+3cd) $$

Разложить на множители многочлен:
81-18p-p²=
\( \frac{1}{9} m²-m{4} \)
Решение: -р²-18р+81=-(р²+18р-81)
квадратный трехчлен
р²+18р-81
имеет дискриминант
D=18²-4·(-81)=324+324=(18√2)²
корни
(-18-18√2)/2=-9-9√2 или (-18+18√2)/2=-9+9√2
и раскладывается на множители
81-18р-р²= - (р+9+9√2)(р+9-9√2)
Скорее всего условие написано с опечаткой.
Должно быть
+р²
81-18p + p²=(9)²-2·9·p+p²=(9-p)² - формула квадрата разности
(1/9)m²-m⁴=m²·((1/9)-m²)=m²·((1/3)-m)·((1/3)+m).
Найти целые корни и разложить на множители многочлен: х^2 + 6х - 7
Решение: По дискриминанту:D=b²-4ac=36+28=64
x₁,₂=-b±√D/2a=-6±8/2
x₁=1
x₂=-7
ответ:1;-7
Если перемножить скобки, которые получились, то: x^2-x+7x-7= x^2+6x-7, значит решено верно!