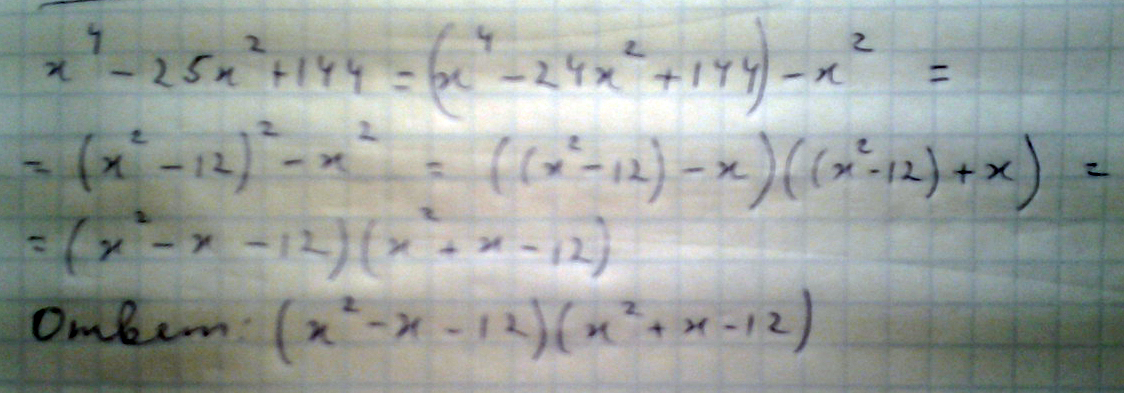разложите многочлен на множители - страница 8
x⁴-25x²+144 - разложить на множители многочлен. Без дискриминантов
Решение: Выделим полный квадрат
x⁴-25x²+144=(x²)²-2*12,5x²+12,5²-12,5²+144=(x²-12,5)²-156,25+144=(x²-12,5)²-12,25=(x²-12,5)²-3,5²=(x²-12,5-3.5)*(x²-12,5+3,5)=(x²-16)*(x²-9)=(x²-4²)*(x²-3²)=(x-4)*(x+4)*(x-3)*(x+3)
x⁴-25x²+144=(x-4)*(x+4)*(x-3)*(x+3)
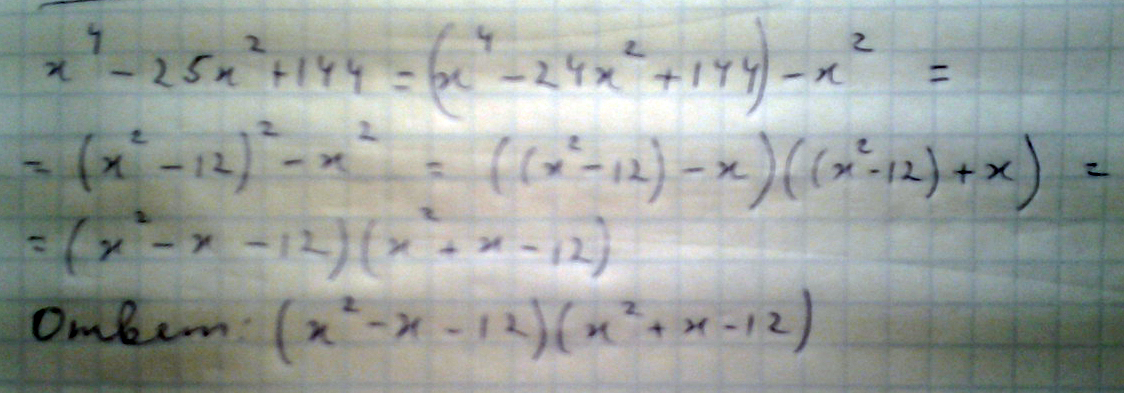
Разложить на множители многочлен: х^4-2х^2-8
Решение: х^4-2х^2-8=x^4-4x^2+2x^2-8=гурппируем(x^4-4x^2)+(2x^2-8)=x^2(x^2-4)+2(x^2-4)==выделяем общий множитель=(x^2+2)(x^2-4)=используем формулу разности квадратов =(x^2+2)(x-2)(x+2)
замена переменных: х в квадрате=t
t в квадрате -2t-8
квадратное ур-е;
t в квадрате-2t-8=0
D=b в квадрате-4ac
D=4+4*8=36
t1=-2
t2=4, значит
(t+2)(t-4) из замены переменных:(x в квадрате+2)(х в квадрате-4)=
=(х в квадрате+2)(х+2)(х-2)
Разложить на множители многочлен: а)xyz+4xz+3xy+12x
б)2а+а^2+2a^3+a^4
в)m^3+m^2n-m^2a-mna
г) b^4-b^3+b^2-b
Решение: а) xyz + 4xz +3xy +12x = xz( y + 4) + 3x( y+4) = (xz+3x)(y+4) = x(z+3)(y+4)б) 2а+а^2+2a^3+a^4 = 2a(1+a^2)+ a^2(1+a^2) = a(2+a)(1+a^2)
в) m^3+m^2n-m^2a-mna = m^2(m+n) - am(m+n) = m(m-a)(m+n)
г) b^4-b^3+b^2-b = b^3(b-1)+ b(b-1) = b(b^2+1)(b-1)
а)xy(z+3)+4x(z+3) = (xy+4x)(z+3) = x(y+4)(z+3)
б)2а(1+а^2)+a^2(1+a^2) = (2a+a^2)(1+а^2) = a(2+a)(1+а^2)
в)m^2(m-a)+mn(m-a) = (m^2+mn)(m-a) = m(m+n)(m-a)
г)b^3(b-1)+b(b-1) = (b^3+b)(b-1) = b(b^2+1)(b-1)
1. Вынести общий множитель за скобки : а) 3х+3у ; б) -7х+ах ; в) 14ab+21a ; г) 25ху²-10х²у
2. Разложить на множители многочлен : а) х³-5х²+3х ; б) 2х³+4х³+6х²
3. Разложить на множители : а) 3(х-2)-5х(х-2) ; б) (5+m)(n-1)-(2m+3)(1-n)
Решение: 1. 3x+3y=3(x+y)
во-первых, у 1 и у 2 есть 3 общая, её можно вынести за скобку получится: 3(x+y)
если мы умножим снова, то получим то же самое, что и было
-7x+ax=x(-7+a)=x(a-7)
есть у обоих слагаемых x, по распределительному закону выносим за скобки
14ab+21a=7*2ab+7*3a=7a(2b+3)
у обоих слагаемых есть 7 и a, выносим за скобку, и остаток просто выписываем
2. х³-5х²+3х=x(x^2-5x+3)
при таком разложении, мы выносим штуку, которая с самой меньшей степенью
2х³+4х³+6х²=2x^3+2*2x^2+3*2x^2=2x^2(x+2x+6)
самая меньшая степень - x^2 и везде есть общая 2
3. а) 3(х-2)-5х(х-2)=(x-2)(3-5x)
здесь уже готовая группировка, здесь по такому же правилу как и там, выносим x-2 за скобки и получаем
б) (5+m)(n-1)-(2m+3)(1-n)=(5+m)(n-1)-(1-n)(2m+3)=(5+m)(n-1)-(n-1)(2m+3)=(5+m)(2m+3)(n-1)
от перемены мест слагаемых сумма не меняется, поэтому переставим1. А)3(х+у)
Б) х(-7+а)
В)7а(2+3)
Г)5ху(5у+2х)
3. А)3х-6-5х(в квадрате)+10х=13x-6-5x(в квадрате)
Б)5n-5+mn-m-2m-2mn-3-3n=2n-8-mn-m
Разложить на множители, используя формулу разности квадратов:
a2 -b2 = (a - b)(a + b)
а) 4x^2 – 1
б) 25x^2 – 9y^2
Используя образец разложить на множители многочлен:
4m2 – 8m = 4m(m – 2)
а) 3x^2 – 6x
б) 5by – y
Разложить на множители данные многочлены. Продумать алгоритм решения.
а) bx^2 - bу^2
б) 5х+5у
в) bc - bd
г) ах^2 + 2аху + ау^2
д) ав^2 - 3в^2 + аву - 3ву
е) ab-a^2b
и) 8m(a-3)+n(a-3)
ж) (p^2-25)-q(p^2-25)
Разложить на множители
а) 3а^2-3в^2
б) 12а^2-4
в) 9x^2 + 18ху + 9у^2
г) -7p^2 + 28pq - 28q^2
д) 8x^3 - 8y^3
Решение: 4x^2 – 1=(2х-1)(2х+1)
25x^2 – 9y^2=(5х-3у)(5х+3у)
3x^2 – 6x=3х(х-2)
5by – y =у(5b-1)
bx^2 - bу^2=b(x-y)(x+y)
5х+5у=5(x+y)
bc - bd=b(c-d)
ах^2 + 2аху + ау^2=a(x+y)²
ав^2 - 3в^2 + аву - 3ву=b(b+y)(a-3)
ab-a^2b=ab(1-a)
8m(a-3)+n(a-3)=(a-3)(8m+n)
(p^2-25)-q(p^2-25)=(p²-25)(1-q)=(p-5)(p+5)(1-q)
3а^2-3в^2=3(a-b)(a+b)
12а^2-4=4(3a²-1)
9x^2 + 18ху + 9у^2=9(x+y)²
-7p^2 + 28pq - 28q^2= -7(p²-4pq+4q²)= -7(p-2q)²
8x^3 - 8y^3= 8(x³-y³)=9(x-y)(x²-xy+b²)