задачи с многочленами - страница 7
Многочлен P(x) дает остаток 2 при делении на x – 1, и остаток 1 при делении на x – 2.
Какой остаток дает P(x) при делении на многочлен (x – 1)(x – 2)?
Решение: Найдем этот многочлен, положим что
$$ P(x)=A(x)(x-1)+2 $$
$$ P(x)=B(x)(x-2)+1 $$
$$ P(x)=C(x)(x-1)(x-2)+d $$
надо найти $$ d $$, положим что $$ A(x)=x-a $$ ; $$ B(x)=x-b $$; $$ P(x)=(x-a)(x-1)+2 $$
$$ P(x)=(x-b)(x-2)+1 $$
$$ (x-a)(x-1)+2=(x-b)(x-2)+1 $$
$$ (b-a+1)x-2b+a=-1 $$
$$ a-b=1 $$ $$ -2b+a=-1 $$
$$ a=1+b $$ $$ -b+1=-1 $$
$$ b=2 $$; $$ a=3 $$
$$ P(x)=(x-3)(x-1)+2 $$
$$ (x-3)(x-1)+2-(x-1)(x-2)=3-x $$
это и есть остаток $$ 3-x $$Дан многочлен P(X)=2x квадрат -4x+9. Докажите, что Р(Х) больше либо равно 0 для любых значений переменной х.
Решение: P(X)=2x^2-4x+9 = 2(x-1)^2+7 >=7, т. к квадрат неотрицательныйI СПОСОБ
P(X) = 2x² - 4x + 9 ≥ 0
Исследуем ф-цию P(X), сначала найдем нули ф-ции:
2x² - 4x + 9 = 0
D = (-4)² - 4*2*9 = 16 - 72 = - 56 < 0 ⇒ ф-ция P(X) ≠ 0 ∀ Х ∈ R.
Значит график нигде не пересекает ось ОХ.
Коэффициент при старшем члене равен 2, т. е. он > 0 ⇒ ветви параболы направлены вверх. Итак, график ф-ции выглядит так как показано на картинке ⇒ P(X) > 0 ∀ Х ∈ R
II СПОСОБ
P(X) = 2x² - 4x + 9 = 2x² - 4x + 2 + 7 = 2(x² - 2х + 1) + 7 = 2(x - 1)² + 7
в данном выражении (x - 1)² ≥ 0 ⇒ 2(x - 1)²≥ 0 и 7 > 0 ⇒
2(x - 1)² + 7 ≥ 0 ∀ Х ∈ R
Ділення многочленів 12х2-5х-7х3+3+3х4/3+х2-2х /-ділення
Решение: Выполнить деление многочленов$$ A=12x^{2}-5x-7x^{3}+3+3x^{4}:3+x^{2}-2x $$
1) Расположим слагаемые в многочленах в порядке убывания степеней переменной х:
делимое $$ 12x^{2}-5x-7x^{3}+3+3x^{4}=3x^{4}-7x^{3}+12x^{2}-5x+3 $$
делитель $$ 3+x^{2}-2x=x^{2}-2x+3 $$
2) Разделим первый член делимого $$ 3x^{4} $$ на первый член делителя $$ x^{2} $$. В результате находим первый член частного $$ 3x^{2} $$
3) Умножим $$ 3x^{2} $$ на делитель и полученный результат $$ 3x^{4}-6x^{3}+9x^{2} $$ вычтем из делимого. Имеем
$$ -x^{3}+3x^{2}-5x+3 $$.
4) Разделим первый член результата $$ -x^{3} $$ на первый член делителя $$ x^{2} $$, находим $$ -x $$ - второй член частного.
5) Умножим второй член частного на делитель и полученное произведение $$ -x^{3}+2x^{2}-3x $$ - вычтем из результата третьего пункта. Имеем
$$ x^{2}-2x+3 $$.
6) Разделим результат $$ x^{2}-2x+3 $$ на делитель $$ x^{2}-2x+3 $$. Получим 1 - третий член частного. Остаток от деления равен 0.
На письме деление выглядит так:
3х⁴-7х³+12х²-5х+3Iх²-2х+3
- 3х⁴-6х³+9х² I3х²-х+1
-х³+3х²-5х+3
- -х³+2х²-3х
х²-2х+3
- х²-2х+3
0
В многочлене 3а^3-1/2a^2+1/3a -1/6 вынесите за скобки указанный множитель
а)1/6 b)1/3 в)-1/2 г)-2
Решение: В многочлене 3а^3-1/2a^2+1/3a -1/6 вынесите за скобки указанный множитель
а)1/6
1/6(18a^3-3a^2+2a-1)
b)1/3
1/3(9a^3-3/2a^2+a-1/2)
в)-1/2
-1.2(-6a^3+a^2-2/3a+1/3)
г)-2
-2(-3/2a^3+1/4a^2-1/6a+1/12)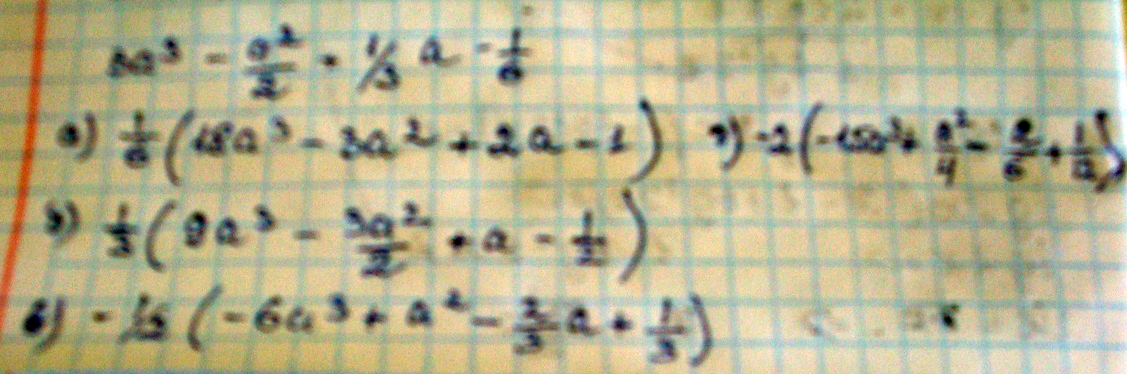
Составьте многочлен p(x) = p1(x) + p2(x) – 4p3(x) и запишите его в стандартном виде, если: p1(x) = - 2x^2 + 3x; p2(x) = 4x^2 – 3; p3(x) = 2x – 4.
Решение: p(x) = p1(x) + p2(x) – 4p3(x)p1(x) = - 2x^2 + 3x; p2(x) = 4x^2 – 3; p3(x) = 2x – 4.
р(х) = (- 2x^2 + 3x) + (4x^2 – 3) - 4(2x – 4)
р(х) = - 2x^2 + 3x + 4x^2 – 3 - 8х +16
р(х) = 2х^2 - 5х - 13
2х^2 - 5х - 13 = 0
p(x) = p1(x) + p2(x) – 4p3(x), если p1(x) = - 2x^2 + 3x; p2(x) = 4x^2 – 3; p3(x)=2x–4, то
p1(x) = 3x + -2x^2
p2 (x) = 4x^2-3
p3 (x) = 2x-4
p(x) = (4x^2-3) + (- 2x^2 + 3x) - 4(2x – 4)
p(x) = 2х^2 - 5х - 13
Ответ: 2x^2-5x -13 =0