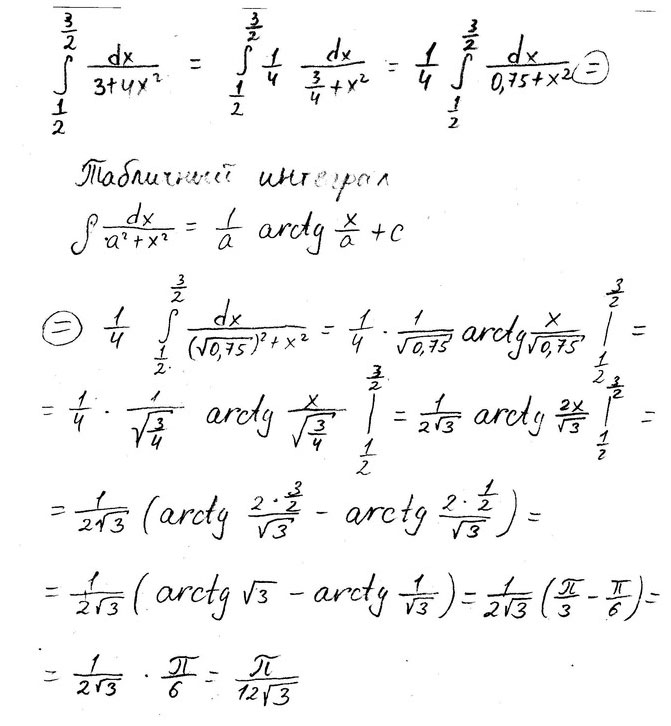интеграл »

определенный интеграл - страница 5

  • Определенный интеграл, с решением, принципа \( \int\limits_{\frac{1}{2}}^1 x^3 exp x^4 dx \)


    Решение: 1. Находим неопределенный интеграл,
    данный интеграл без проблем берется "подведением под знак дифференциала" 
    $$ x^3dx = \frac{1}{4} dx^4, \\ \int\limits {x^3 exp(x^4) } \, dx = \frac{1}{4} \int\limits {exp(x^4) } \, dx^4, \\ u = x^4 \\ \frac{1}{4} \int\limits {exp(u) } \, du = \frac{1}{4} exp(u) = \frac{1}{4} exp(x^4) + const $$
    2. Находим определенный интеграл, используя формулу Ньютона-Лейбница:
    $$ = \frac{1}{4} (exp(1) - exp( \frac{1^4}{2^4} ) ) = 1/4 (e - e^ \frac{1}{16} ) $$

  • Определенный интеграл \( \int\limits^{3/2}_{1/2} { \frac{dx}{3+4x^2} } \)


    Решение: $$ \int\limits^{3/2}_{1/2} { \frac{dx}{3+4x^2} } = \frac{1}{4} \int\limits^{3/2}_{1/2} { \frac{dx}{3/4+x^2} } = \frac{1}{4} \int\limits^{3/2}_{1/2} { \frac{dx}{ (\sqrt{3} /2)^2+x^2} } = \\ \frac{1}{4} \frac{1}{ \sqrt{3}/2 }arctg \frac{x}{ \sqrt{3}/2}|\int\limits^{3/2}_{1/2}= \frac{ \sqrt{3}}{6}(arctg \frac{3/2}{ \sqrt{3}/2 } -arctg \frac{1/2}{ \sqrt{3}/2 })= \\ \frac{ \sqrt{3}}{6}(arctg \sqrt{3} -arctg \frac{ \sqrt{3} }{ 3})=\frac{ \sqrt{3}}{6}( \pi /3- \pi /6)=\frac{ \sqrt{3}}{6}* \pi /6= \frac{ \sqrt{3} \pi }{36} $$

    Решение в приложении

    int limits frac dx x frac int limits frac dx x frac int limits frac dx sqrt x frac frac sqrt arctg frac x sqrt int limits frac sqrt arctg frac sqrt -arctg frac sqrt frac sqrt...

  • Найти определенный интеграл \( 1)\; \int_0^1\frac{8arctgx-x}{1+x^2}dx\\ 2)\; \int _1^{e}\frac{x^8+lnx^9+1}{x}dx= \)


    Решение: $$ 1)\; \int_0^1\frac{8arctgx-x}{1+x^2}dx=8\int _0^1arctgx\cdot \frac{dx}{1+x^2}-\frac{1}{2}\int _0^1\frac{2xdx}{1+x^2}=\\\\=[t=arctgx,\; u=1+x^2=8\cdot \int _0^{\frac{\pi}{4}}t\cdot dt-\frac{1}{2}\int _1^2\frac{du}{u}=8\frac{t^2}{2}|_0^{\frac{\pi}{4}}-\frac{1}{2}ln|u||_1^2\\\\=4\cdot \frac{\pi ^2}{16}-\frac{1}{2}(ln2-ln1)=\frac{\pi ^2}{4}-\frac{1}{2}ln2\\\\\\2)\; \int _1^{e}\frac{x^8+lnx^9+1}{x}dx=\int _1^{e}(x^7+\frac{9lnx}{x}+\frac{1}{x})dx=(\frac{x^8}{8}+9\frac{ln^2x}{2}+ln|x|)|_1^{e}= \\ =\frac{e^8}{8}+\frac{9}{2}+1-\frac{1}{8} $$

  • Решите определенный интеграл \( \int\limits^4_2 {(x^2-5x+6)} \, dx \)


    Решение: $$ \int\limits^4_2 {(x^2-5x+6)} \, dx = \frac{x^3}{3} -5* \frac{x^2}{2} +6x|^4_2= \\ \\ =( \frac{4^3}{3} -5* \frac{4^2}{2} +6*4)-( \frac{2^3}{3} -5* \frac{2^2}{2} +6*2)= \\ \\ =( \frac{64}{3} -5* \frac{16}{2} +24)-( \frac{8}{3} -5* \frac{4}{2} +12)= \\ \\ =( \frac{64}{3} -5*8 +24)-( \frac{8}{3} -5* 2 +12)= \\ \\ =( \frac{64}{3} -40 +24)-( \frac{8}{3} -10 +12)= \\ \\ =( \frac{64-40*3+24*3}{3})-( \frac{8-10*3+12*3}{3})= \\ \\ \\ =( \frac{64-120+72}{3})-( \frac{8-30+36}{3})= \\ \\ = \frac{16}{3}- \frac{14}{3}= \\ \\ =\frac{2}{3} $$

  • Решить определенный интеграл \( 1)\; \; \int _0^2(3x+3\sqrt{x}-\sqrt{x^3})dx\\ 2)\quad \int _1^2(1-x)^3dx \)


    Решение: $$ 1)\; \; \int _0^2(3x+3\sqrt{x}-\sqrt{x^3})dx=(3\cdot \frac{x^2}{2}+3\cdot \frac{x^{\frac{3}{2}}}{\frac{3}{2}}-\frac{x^{\frac{5}{2}}}{\frac{5}{2}})|_0^2=\\\\=(\frac{3}{2}x^2+2\sqrt{x^3}-\frac{2}{5}\sqrt{x^5})_0^2=\frac{3}{2}\cdot 4+2\sqrt{2^3}-\frac{2}{5}\sqrt{2^5}=\\\\=6+4\sqrt2-\frac{8}{5}\sqrt2=6+\frac{12}{5}\sqrt2 \\ 2)\quad \int _1^2(1-x)^3dx=[\, t=1-x\;,\; dt=-dx\;,\\\\ t_1=1-1=0,\; \; t_2=1-2=-1\, ]=\\\\=-\int _0^{-1}t^3\, dt=-\frac{t^4}{4}|_0^{-1}=-\frac{1}{4}((-1)^4-0^4)=-\frac{1}{4} $$

<< < 345 6 7 > >>