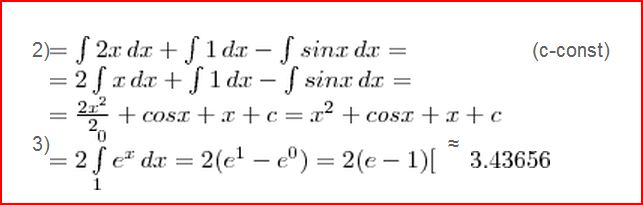интеграл »

неопределенный интеграл - страница 10

  • Вычислить неопределенный интеграл, желательно без всяких логарифмов \( \int\limits \frac{cos(x)dx}{2sin(x) +1} \)


    Решение: Здесь никак нельзя без логарифма

    Допустим, u=2sin(x)+1
    u=2sin⁡(x)+1
    du=2cosxdxdu=2cos⁡xdx и подставим $$ \frac{du}{2} \\ \int\ { \frac{1}{u} } \, du \\ \int\ { \frac{1}{u} } \, du = \frac{1}{2} \\ \int\ { \frac{1}{u} } \, du $$

    Интеграл $$ \frac{1}{u} = logu =>  \frac{1}{2}logu $$

    Дальше? Или не устраивает с логарифмом?)

    ∫(cos(x)/(2sin(x)+1))dx = ∫d(sin(x))/(2sin(x)+1) = 1/2*∫d(2sin(x)+1)/(2sin(x)+1)=1/2*ln|2sin(x)+1| + C

  • Вычислить неопределенный интеграл \( \int \frac{x^4\, dx}{x^5+7} \) и определенный \( \int _{\frac{\sqrt3}{3}}^{\frac{2\sqrt3}{3}}\,\frac{9dx}{\sqrt{4-3x^2}} \)


    Решение: $$ \int \frac{x^4\, dx}{x^5+7}=[t=x^5+7,\; dt=5x^4dx]=\frac{1}{5}\int \frac{dt}{t}=\frac{1}{5}ln|t|+C=\\\\=\frac{1}{5}ln|x^5+7|+C\\\\\\\int _{\frac{\sqrt3}{3}}^{\frac{2\sqrt3}{3}}\,\frac{9dx}{\sqrt{4-3x^2}}=\int _{.}^{.}\frac{9dx}{\sqrt{2^2-(\sqrt3x)^2}}=\\\\=[t=\sqrt3x,dt=\sqrt3dx,\\\\\int \frac{9\cdot \frac{dt}{\sqrt3}}{\sqrt{2^2-t^2}}=3\sqrt3\int \frac{dt}{\sqrt{2^2-t^2}}=3\sqrt3\cdot arcsin\frac{t}{2}+C]=\\\\=3\sqrt3\cdot arcsin\frac{\sqrt3x}{2}\, |_{\frac{\sqrt3}{3}}^{\frac{2\sqrt3}{3}}= \\ =3\sqrt3(arcsin1-arcsin\frac{1}{2})=3\sqrt3(\frac{\pi}{2}-\frac{\pi}{6})=3\sqrt3\cdot \frac{\pi}{3}=\pi \sqrt3 $$

  • 1 - найти неопределенный интеграл \(\int(2x-sinx+1)dx \)
    2 - вычислите определенный интеграл \( \int\limits_0^1 e^x dx \)


    Решение: 2)$$ = \int\limits {2x} \, dx + \int\limits {1} \, dx - \int\limits {sin x} \, dx= \\ =2\int\limits {x} \, dx + \int\limits {1} \, dx - \int\limits {sin x} \, dx= \\ = \frac{2x^2}{2} +cos x+x+c=x^2+cos x+x+c $$ (c-const)
    3)$$ =2 \int\limits^0_1 {e^x} \, dx =2(e^1-e^0)=2(e-1)[ $$ ≈ $$ 3.43656 $$

    2) $$ \int\limits {(2x-sin x +1)} \, dx =x^2+cos x +x+C $$
     
    3) $$ \int\limits^1_0 {2 e^{x} } \, dx=2 e^{x} $$|1;0=2(e-1)≈3,43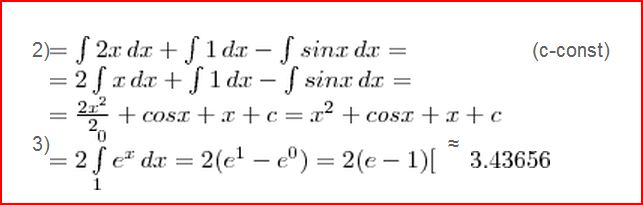

    int limits x dx int limits dx - int limits sin x dx int limits x dx int limits dx - int limits sin x dx frac x cos x x c x cos x x c c-const int limits e x dx e -e e- .   int...

  • найти неопределенный интеграл:

    инт(x^3dx/корень(x-7))


    Решение: Решенние:

    инт(x^3dx/корень(x-7))=|корень(x-7)=t x=t^2+7 dx=2tdt|=

    =инт((t^2+7)^3 *2t \t) dt=

    =2*инт((t^6+21t^4+147t^2+343)dt=

    =2*(1\7t^7+21\5t^5+49t^3+343t)+c=

    =2\7*t^7+42\5t^5+98t^3+686t+c=

    =2\7*(корень(x-7))^7+42\5*(корень(x-7))^5+98*(корень(x-7))^3+686*(корень(x-7))+c, где с произвольная константа

    Ответ:2\7*(корень(x-7))^7+42\5*(корень(x-7))^5+98*(корень(x-7))^3+686*(корень(x-7))+c, где с произвольная константа

  • Найти неопределенный интеграл cos(5lnx)


    Решение: $$ I = \int \cos(5lnx) dx = [lnx = t, \ x = e^{t}, \ \frac{1}{x}dx = dt] =\\\\ \int e^{t}\cos(5t)dt = e^{t}\cos(5t) + 5\int e^{t}\sin(5t)dt =\\\\ e^{t}\cos(5t) + 5e^t\sin(5t) - 25\int e^t\cos(5t) dt\\\\ I = e^{t}\cos(5t) + 5e^t\sin(5t) + C - 25I\\\\ 26I = e^{t}\cos(5t) + 5e^t\sin(5t) + C\\\\ I = \frac{1}{26}(e^{t}\cos(5t) + 5e^t\sin(5t)) + \frac{C}{26}, \ \frac{C}{26} = C_1\\\\ I = \frac{1}{26}e^t(\cos(5t) + 5\sin(5t)) + C_1\\\\ \boxed{I = \frac{x}{26}(\cos(5lnx) + 5\sin(5lnx)) + C_1 } $$

<< < 8910 11 12 > >>