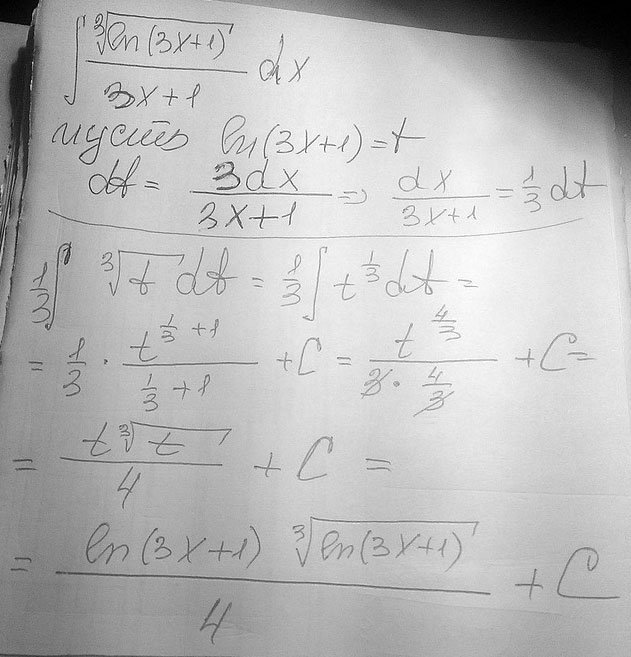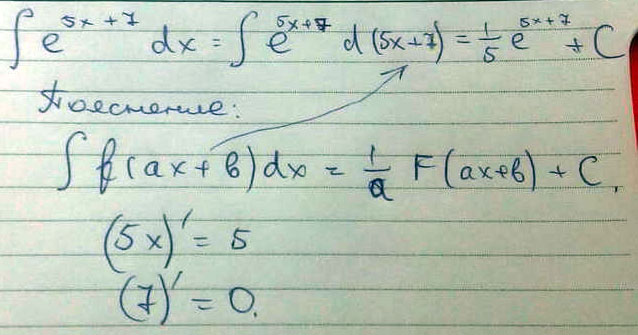интеграл »
неопределенный интеграл - страница 11
Найти неопределенный интеграл \( \int e^{sin3x}cos3x dx \)
Решение: Прием называется введение под знак дифференциала
заметим что cos(3x)*dx = 1/3*cos(3x)*d(3x)=1/3*d(sin(3x))
действительно, (1/3*sin(3x))` = cos(3x)
тогда
integral e^(sin(3x))*cos(3x)dx = 1/3*integral e^(sin(3x))*d(sin(3x)) =1/3*integral e^y*dy = 1/3*(e^y+C) =1/3*e^y+C =1/3*e^(sin(3x))+C
******************************
при расчетах использовалась переменная у = (sin(3x))
Найти неопределенный интеграл \(\int\limits { \sqrt[3]{ln(3x+1)} /(3x+1)} \, dx \)
Решение:Ln(3x+1)=t⇒dt=3dx/(3x+1)⇒dx/(3x+1)=dt/3
$$ \int\limits { \sqrt[3]{ln(3x+1)} /(3x+1)} \, dx =1/3 \int\limits { \sqrt[n]{t} } \, dt =1/3*3/4 \sqrt[3]{t^4} = \ 1/4* \sqrt[3]{ln^4(3x+1)} +C $$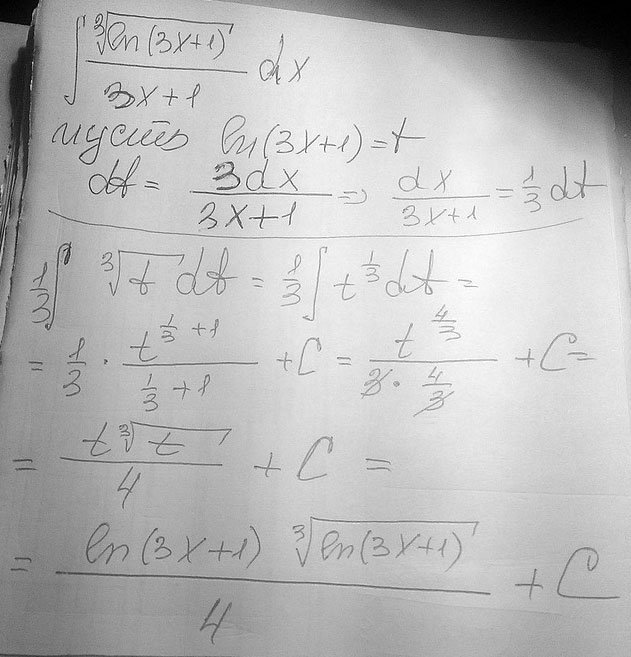
Найти неопределенный интеграл \(\int\limits {e^{5x+7}} \, dx\)
Решение: $$ \int\limits {e^{5x+7}} \, dx = \int\limits {\frac{e^{5x+7}}5} \, d(5x+7) =\frac{e^{5x+7}}5+C $$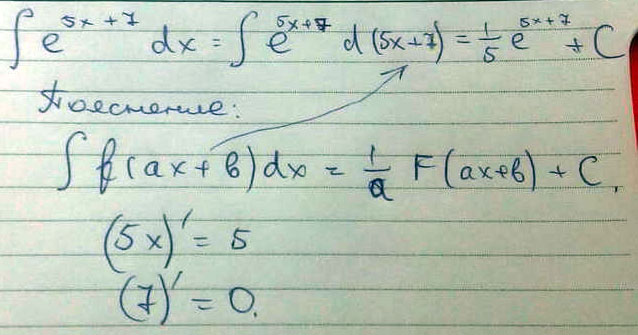
Найти неопределенный интеграл
xln(x^2+2)dx
Решение: Замена переменной:
t=x²+2, dt=2x dx⇒ xdx= dt/2 и интегрирование по частям:
Тогда $$ \int\limits{xln( x^{2} +2)} \, dx= \int\limits{lnt} \frac{dt}{2} \, = \left[{u=lnt \atop {dv=dt}} \right. \left[ {{du= \frac{1}{t} dt} \atop {v=t2}} \right]= \\ = \frac{1}{2} (t\cdot lnt- \int\limits {t \frac{1}{t} } \, dt)= \frac{1}{2}(t\cdot lnt-t)=[t= x^{2} +2]= \\ = \frac{1}{2} ( ( x^{2} +2)ln( x^{2} +2)-( x^{2} +2)) +C $$
Найти неопределенный интеграл \(\int\limits \frac{2x^{10}+3 \sqrt[5]{x}-1 }{2x^2} dx\\ \int\limits \frac{ \sqrt[7]{ln^2(x+1)} }{x+1} dx \)
Решение: $$ \int\limits \frac{2x^{10}+3 \sqrt[5]{x}-1 }{2x^2} dx= \int\limits( \frac{2x^{10} }{2x^2} +\frac{3 \sqrt[5]{x} }{2x^2}-\frac{1 }{2x^2} )dx= \\ = \int\limits x^8dx + \frac{3}{2} \int\limits x^{-1.8}dx- \frac{1}{2} \int\limits x^{-2}dx= \\ = \frac{x^9}{9} + \frac{3}{2} * \frac{x^{-0.8}}{-0.8} - \frac{1}{2} * \frac{x^{-1}}{-1} +C= \frac{x^9}{9} - \frac{3}{1.6x^{0.8}} + \frac{1}{2x} +C \\ \int\limits \frac{ \sqrt[7]{ln^2(x+1)} }{x+1} dx= \int\limits \frac{ \sqrt[7]{ln^2(x+1)} }{x+1} d(x+1)= \int\limits \sqrt[7]{ln^2(x+1)} d(ln(x+1))= \\ = \int\limits ln^{ \frac{2}{7} }(x+1) d(ln(x+1))= \frac{ ln^{ \frac{9}{7} }(x+1)}{ \frac{9}{7} } +C= \frac{7 ln^{ \frac{9}{7} }(x+1)}{9 } +C $$