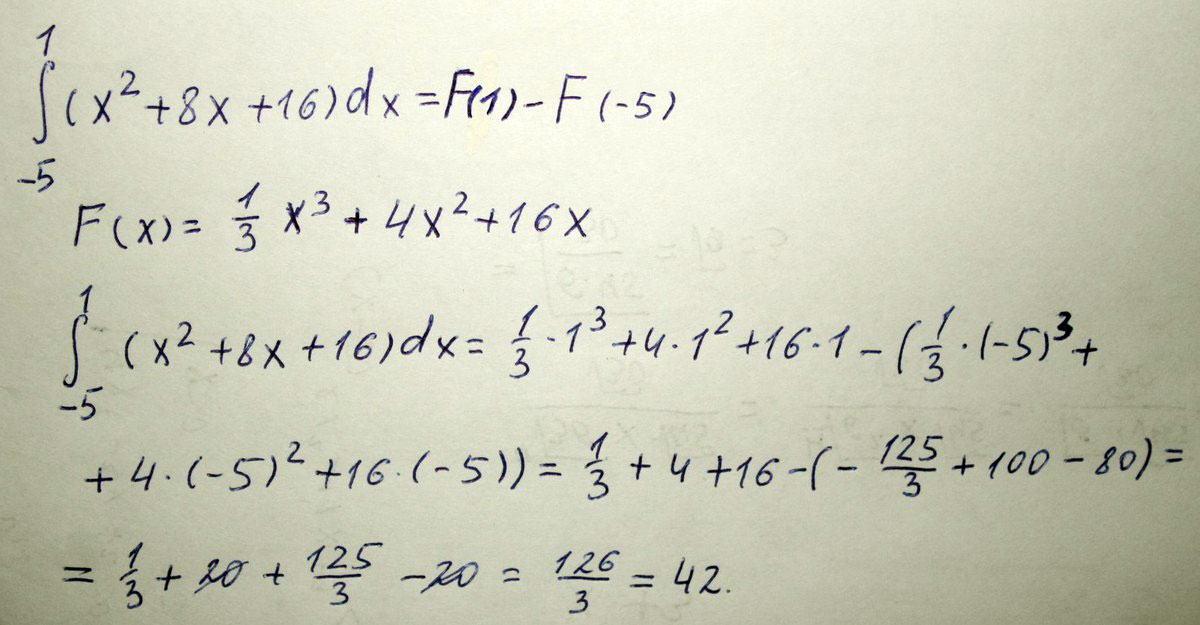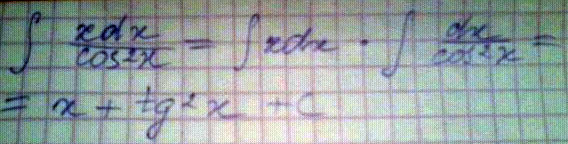интеграл »
найти интеграл - страница 23
Интеграл 3х.
Решение: S3xdx=3*(x¹⁺¹)/(1+1)+C=3x²/2+C=1,5x²+CЭто просто табличный интеграл от степенной функции. Выносите тройку за знак интеграла, у вас останется только х. Применяем формулу: (x^n)dx=(x^n+1)/(n+1)+C. В данном случае степень равна единице, следовательно: (x^1+1)/(1+1) получается x^2/2, НО не забываем про тройку, которую вынесли и домнажаем. Получаем ответ: 3x^2/2+C
Интеграл от 1 до -5 ( x^2+8x+16)dx
Решить
Решение: $$ \int _1^{-5}\, (x^2+8x+16)\, dx=(\frac{x^3}{3}+8\frac{x^2}{2}+16x)|_1^{-5}=\\\\=\frac{(-5)^3}{3}+4(-5)^2+16(-5)-(\frac{1}{3}+4+16)=\\\\=-\frac{125}{3}+100-80-\frac{1}{3}-4-16=-42 $$Полное решение задания в файле.
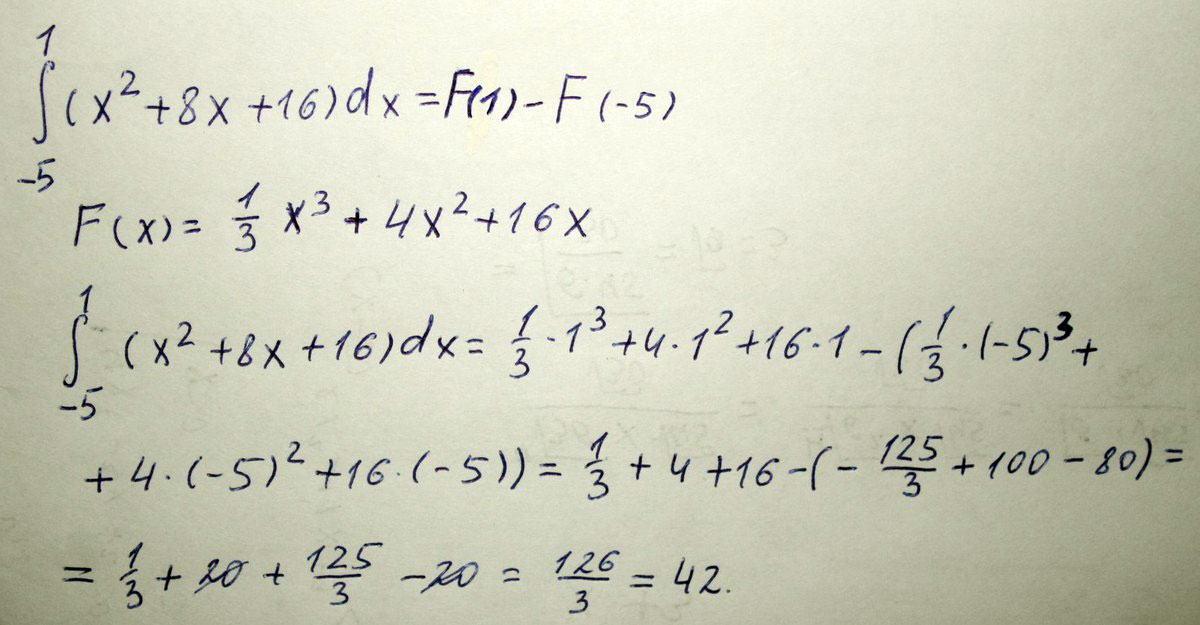
Интеграл xdx/cos^2 (x)
Решение: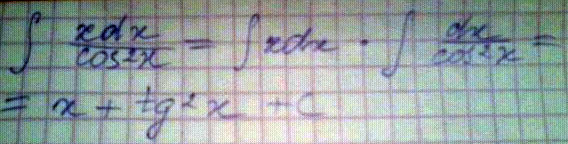
Найти интеграл \( \int\limits{ \frac{ \sqrt{x} }{1- \sqrt[3]{x} } } \, dx \)
Решение: $$ \int\limits{ \frac{ \sqrt{x} }{1- \sqrt[3]{x} } } \, dx=[ \sqrt[6]{x}=t\Rightarrow x=t ^{6}\Rightarrow dx=6t ^{5}dt || \sqrt[3]{x}=t ^{2}, \sqrt{x} =t ^{3}] = \\ = \int\limits{ \frac{ t ^{3} }{1- t ^{2} } }\,6t ^{5} dt=6 \int\limits{ \frac{ t ^{8} }{1- t ^{2} } } \,dt=-6 \int\limits(t ^{6}+t ^{4}+t ^{2}+1+ \frac{1}{t ^{2}-1 })dt= \\ =-6 \cdot\frac{t ^{7} }{7}-6\cdot \frac{t^{5} }{5} -6 \frac{t ^{3} }{3}-6t-6\cdot \frac{1}{2}ln| \frac{t-1}{t+1}|+C= \\ = \\ =-6 \cdot\frac{ \sqrt[6]{x} ^{7} }{7}-6\cdot \frac{ \sqrt[6]{x} ^{5} }{5} -6 \frac{ \sqrt[6]{x} ^{3} }{3}-6 \sqrt[6]{x} -6\cdot \frac{1}{2}ln| \frac{ \sqrt[6]{x} -1}{ \sqrt[6]{x} +1}|+C $$
Найдите интеграл \( \int\frac{dx}{2sinx-cosx +5} \)
Решение: Замена переменной
$$ tg \frac{x}{2}=t $$
Тогда
$$ sinx= \frac{2t}{1+t ^{2} }; \\ cosx= \frac{1-t ^{2} }{1+t ^{2} } ; \\ dx= \frac{2dt}{1+t ^{2} } $$
Подынтегральная дробь примет вид:
$$ \frac{dx}{2sinx-cosx+5}= \frac{ \frac{2dt}{1+t ^{2} } }{2\cdot \frac{2t}{1+t ^{2} }- \frac{1-t ^{2} }{1+t ^{2} }+5 } = \\ = \frac{2dt}{4t-1+t ^{2}+5+5t ^{2} }=\frac{2dt}{6t ^{2}+4t+4 }= \frac{dt}{3t ^{2}+2t+2 } $$
Выделим полный квадрат в знаменателе:
$$ 3t ^{2}+2t+2=3(t ^{2}+ \frac{2}{3}t+ \frac{2}{3})=3(t ^{2}+2\cdot t\cdot \frac{1}{3}+ \frac{1}{9}- \frac{1}{9}+ \frac{4}{9})= \\ = 3(t+ \frac{1}{3}) ^{2} +3\cdot \frac{3}{9}=3(t+ \frac{1}{3})x^{2}+1=3((t+ \frac{1}{3}) ^{2} + \frac{1}{3}) $$
Итак,
$$ \int\limits { \frac{dt}{3((t+ \frac{1}{3}) ^{2}+ \frac{1}{3})} } = \frac{1}{3} \int\limits { \frac{d(t+ \frac{1}{3}) }{(t+ \frac{1}{3}) ^{2}+ \frac{1}{3} } } = \frac{1}{3}\cdot \frac{1}{ \sqrt{ \frac{1}{3} } } arctg \frac{t+ \frac{1}{3} }{ \sqrt{ \frac{1}{3} } }+C = \\ = \frac{ \sqrt{3} }{3}arctg( \sqrt{3}tg \frac{x}{2}+ \frac{ \sqrt{3} }{3}) +C $$