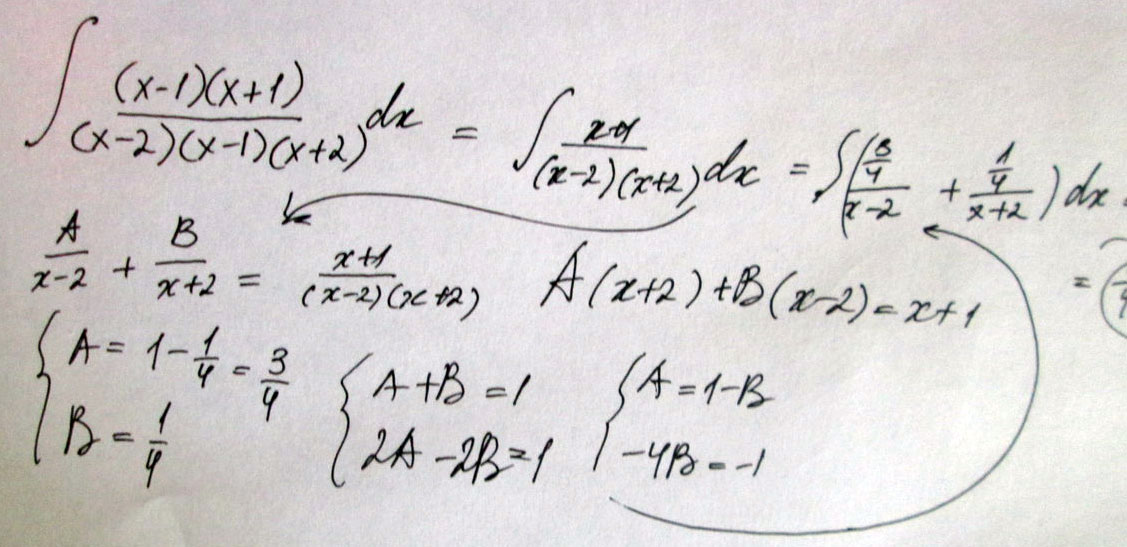интеграл »
найти интеграл - страница 22
Интеграл \( \int{\frac{x^3-1}{x+1}} \, dx \)
Решение: $$ \int{\frac{x^3-1}{x+1} \, dx = \int\ {(\frac{x^3}{x+1} - \frac{1}{x+1}) } \, dx = \int\ {\frac{x^3}{x+1} \, dx - \int \frac{1}{x+1} }} \, dx= \\ \\ = \int\ {\frac{x^2 \cdot (x+1) -x \cdot (x+1)+(x+1)-1}{x+1} \, dx - \int \frac{1}{x+1} } \, dx= \\ \\ = \int\ {(x^2 -x +1-\frac{1}{x+1}) \, dx - \ln{|x+1|}} =\\ \\ = \int\ {x^2} \, dx - \int\ {x } \, dx + \int\ {1} \, dx - \int\ {\frac{1}{x+1}} \, dx- \ln{|x+1|}= \\ \\ = \frac{x^3}{3}-\frac{x^2}{2}+x-\ln{|x+1|}-\ln{|x+1|}+C= \ \\ \\ = \frac{x^3}{3}-\frac{x^2}{2}+x-2\ln{|x+1|}+C= $$Интеграл \( \int\frac{(x^2-1)dx}{(x-2)(x^2+x-2)} \)
Решение: $$ \int \frac{(x-1) \cdot (x+1)}{(x-2) \cdot (x-1) \cdot (x+2)} \, dx= \int \frac{ x+1}{(x-2)\cdot (x+2)} \, dx = (*) \\ \\ \frac{A}{x-2} + \frac{B}{x+2}=\frac{x+1}{(x-2)\cdot (x+2)} \\ \\ A(x+2) + B(x-2)=x+1 \\ \\ \left\{\!\begin{aligned} & A+B=1 \\ & 2A-2B=1 \end{aligned}\right. \ \ \ \left\{\!\begin{aligned} & A=1-B \\ & 2-2B-2B=1 \end{aligned}\right. \ \ \ \left\{\!\begin{aligned} & A = 1-B \\ & -4B=-1 \end{aligned}\right. \\ \ \left\{\!\begin{aligned} & A = 1-\frac{1}{4}=\frac{3}{4} \\ & B=\frac{1}{4} \end{aligned}\right. \\ (*) = \int {( \frac{\frac{3}{4} }{x-2} + \frac{\frac{1}{4}}{x+2})} \, dx = \\ \\ = \frac{3}{4} \int {\frac{\, dx}{x-2}} + \frac{1}{4} \int {\frac{ \, dx }{x+2}}= \\\\=\frac{3}{4}\cdot \ln{|x-2|}+\frac{1}{4} \cdot \ln{|x+2|}+C $$
Решение в файле.
Интеграл \( \int \frac{\sqrt{x} -5x^4+ 6}{x^{\frac{2}{3}}} \, dx \)
Решение: Разложим дробь и упростим, используя свойство степеней $$ \frac{x^m}{x^n}=x^{m-n} $$
Найдем интеграл по формуле $$ \int {x^n} \, dx= \frac{x^{n+1}}{n+1}+C \\ \int \frac{\sqrt{x} -5x^4+ 6}{x^{\frac{2}{3}}} \, dx = \\ \\= \int (\frac{x^{\frac{1}{2}}}{x^{\frac{2}{3}}}- \frac{5x^4}{x^{\frac{2}{3}}}+\frac{6}{x^{\frac{2}{3}}}) \, dx = \\ \\ = \int x^{-\frac{1}{6}} \, dx-5 \int x^{\frac{10}{3}} \, dx + 6\int {x^{-\frac{2}{3}}} \, dx= \\ \\= \frac{x^{\frac{5}{6}}}{\frac{5}{6}} - 5 \cdot \frac{x^{\frac{13}{3}}}{\frac{13}{3}}+ 6 \cdot \frac{x^{\frac{1}{3}}}{\frac{1}{3}}+C= \\ \\ \ = \frac{6}{5} \cdot x^{\frac{5}{6}} - \frac{15}{13} \cdot x^{\frac{13}{3}}+ 18 \cdot x^{\frac{1}{3}}+C $$
Интеграл \(\int _3^{+\infty}\frac{dx}{e^{\frac{x}{3}}}\)
Решение: $$ \int\limits {e^{-x/3}} \, dx = -3e^{-x/3} + Const $$ (можете проверить, продифференцировав)
Откуда, пользуясь формулой Ньютона - Лейбница, находим значение определённого интеграла. $$ -3e^{-\infty/3} - (-3e^{-3/3}) = 0 - (-3/e) = 3/e $$
$$ \int _3^{+\infty}\frac{dx}{e^{\frac{x}{3}}}=lim_{b\to +\infty}\int _3^{b}\, e^{-\frac{x}{3}}\, dx=-3\cdot lim_{x\to +\infty }\int _3^{b}e^{-\frac{x}{3}}dx=\\\\=-3\cdot lim_{x\to +\infty }\int _3^{b}e^{-\frac{x}{3}}\, d(-\frac{x}{3})=-3\cdot lim_{x\to +\infty }e^{-\frac{x}{3}}\, |_3^{b}=\\\\=-3lim_{x\to +\infty }(e^{\frac{-b}{3}}-e^{-1})=-3\cdot (0-\frac{1}{e})=\frac{3}{e}=const\; \; \to \; \; sxoditsya \\ P.S.\; lim_{x\to \infty}e^{x}= \left \{ {{0,esli\; x\to -\infty } \atop {+\infty,esli\; x\to +\infty}} \right. $$
Интеграл \( \int\limits_0^5 \frac{dx}{2+\sqrt(x+4)} \)
Решение: $$ \int\limits^5_0 { \frac{\, dx }{2+ \sqrt{x+4} } } = $$
замена х+4=у², dx=2ydy, у изменяется от 2 до 3
$$ \int\limits^3_2 { \frac{2y\, dy }{2+ y } } = 2\int\limits^3_2 { \frac{(y+2-2)\, dy }{2+ y } } =\\= 2 \int\limits^3_2 { \frac{(y+2)\, dy }{2+ y } }-2 \int\limits^3_2 { \frac{\, dy }{2+ y } } = 2\int\limits^3_2 {\, dy } -4\int\limits^3_2 { \frac{\, d(2+y) }{2+ y } } = \\ 2y|\int\limits^3_2 {\, dy } -4ln|2+y||\int\limits^3_2 =6-4-4(ln5-ln4)=2-4ln1.25 $$