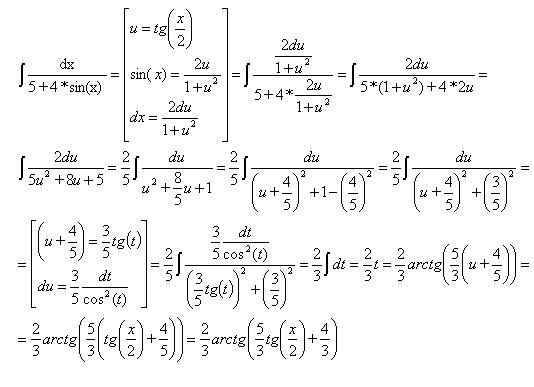интеграл »
найти интеграл - страница 24
Найти интеграл при помощи универсальной тригонометрической подстановки
1/(5+4*sin(x))
Решение: Универсальная тригонометрическая подстановка:
$$ \frac{dx}{dt} = \frac{2dt}{1+t^2} \\ sinx= \frac{2t}{1+t^2} \\ \int\limits {\frac{dx}{5+4sinx} }= \int\limits \frac{2dt}{(1+t^2)(5+4 \frac{2t}{1+t^2} )} = 2 \int\limits \frac{dt}{5(1+t^2)+8t}= 2 \int\limits \frac{dt}{5t^2+8t+5} $$
Это табличный интеграл (если в вашей таблице его нет, напиши, будет его подробнее вычислять)
$$ b^2-4ac=8^2-4*5*5=64-100=-36 $$
При отрицательном значении формула имеет вид
$$ 2 \int\limits \frac{dt}{5t^2+8t+5}= 2*\frac{2}{ \sqrt{4ac-b^2} } arctg( \frac{2ax+b}{ \sqrt{4ac-b^2} } )+C= \\ =\frac{4}{ \sqrt{4*5*5-8^2} } arctg( \frac{2*5x+8}{ \sqrt{100-64} } )+C= \\ =\frac{4}{6 } arctg( \frac{10x+8}{ 6 } )+C=\frac{2}{3 } arctg( \frac{10x+8}{ 6 } )+C $$
на картинке
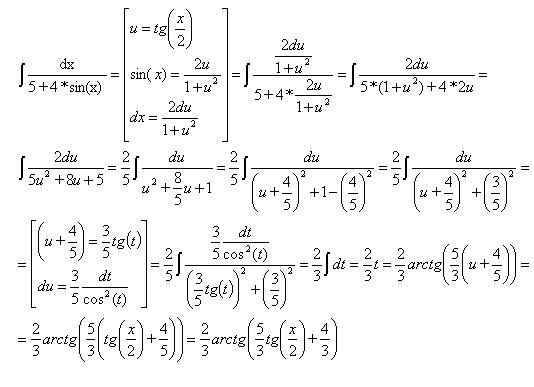
Найти интеграл sin^2x*cos^2x dx
Решение: $$ Sin^2x\cdot Cos^2x=(Sinx\cdot Cosx)(Sinx\cdot Cosx)=\frac{1}{4}(Sin2x)(Sin2x)= \\ =\frac{1}{4}Sin^22x \\ Cos^2\alpha -Sin^2\alpha=Cos2\alpha \ \ => \ \ 1-2Sin^2\alpha=Cos2\alpha \ \ => \\ => \ \ Sin^2\alpha=\frac{1+Cos2\alpha}{2} \\ \int {Sin^2x\cdot Cos^2x} \, dx =\frac{1}{8}\int {(1+Cos4x)dx=\frac{1}{8}( \int{}dx+\int{Cos4x}dx)} \\ \int {}dx=x \\ \int {Cos4x} dx: \\ 4x=u \ \ => \ \ 4xdx=du \ \ => \ \ \frac{du}{4}=dx \ \ => \\ => \ \ \int{Cos4x}dx=\frac{1}{4}\int{Cosu}du=\frac{Sinu}{4}=\frac{Sin4x}{4} \\ \int {Cos4x} dx=\frac{Sin4x}{4} \\ \frac{1}{8}(\int{}dx+\int{Cos4x}dx)=\frac{1}{8}(x+\frac{Sin4x}{4}) $$
Найти интеграл \( \int\limits^{1}_{-1}(2 - 2x^2) \ dx \)
Решение: $$ \int\limits^{1}_{-1}(2 - 2x^2) \ dx = (2x - \frac{2}{3}x^3) |^{1}_{-1} = (2 - \frac{2}{3}) - (-2 +\frac{2}{3}) = 4 - \frac{4}{3} = \boxed{\frac{8}{3}} $$
Для решения определенных интегралов используется формула Ньютона-Лейбница:
$$ \int\limits^{b}_{a} f(x) = F(b) - F(a) $$
F(x) первообразная функции f(x).
Само собой, ищем мы её находя неопределенный интеграл:
$$ \int f(x) \ dx = F(x) + C $$
В нашем случае:
$$ \int (2 - 2x^2) \ dx= \int 2 \ dx - 2\int x^2 \ dx = 2x - \frac{2x^3}{3} +C $$
Используя, что:
$$ \int c*f(x) \ dx = c*\int f(x) \ dx, \ c e 0\\\\ \int f(x) + g(x) \ dx = \int f(x) \ dx+ \int g(x) \ dx\\\\ \int c \ dx = cx + C\\\\ \int x^n \ dx = \frac{x^{n+1}}{n+1} + C $$
Найти интеграл от икса умноженного на арксинус икс ∫(x*arcsin(x)dx
Решение: ∫(x*arcsin(x)dxПусть
u=arcsin(x) du=dx/√(1-x^2)
dv=xdx v=x^2/2
Далее интегрируем по частям
∫(x*arcsin(x)dx=x^2*arcsin(x)/2 -(1/2)*∫(x²dx/√(1-x²)=
Пусть
x=sin(t)
dx=cos(t)
=x²*arcsin(x)/2 -(1/2)*∫(sin²(u)cos(u)du/√(1-sin²(u))=
=x²*arcsin(x)/2 -(1/2)*∫(sin²(u)cos(u)du/cos(u))=
=x²*arcsin(x)/2 -(1/2)*∫(sin²(u)du=
=x²*arcsin(x)/2 -(1/4)*∫(1-cos(2u)du=
=x²*arcsin(x)/2 -du/4 +(1/4)*∫cos(2u)du=
=x²*arcsin(x)/2 -u/4 +(1/8)*sin(2u)+c=
=x²*arcsin(x)/2 -arcsin(x)/4 +(x*√(1-x²)/4)*sin(2u)+c
Найти интеграл
\( \frac{\sqrt{x^2+4}}{x^2} \)
Решение: $$ \int \frac{\sqrt{x^2 + 4}}{x^2} \ dx = \int \frac{x^2 + 4}{x^2\sqrt{x^2 + 4}} \ dx =\\\\ \int \frac{x^2}{x^2\sqrt{x^2 + 4}} \ dx + \int \frac{4}{x^2\sqrt{x^2 + 4}} \ dx =\\\\ \int \frac{1}{\sqrt{x^2 + 4}} \ dx + \int \frac{4}{x^2\sqrt{x^2 + 4}} \ dx \\ 1) \ \int \frac{1}{\sqrt{x^2 + 4}} \ dx = ln|x + \sqrt{x^2 + 4}| + C \\ 2) \int \frac{4}{x^2\sqrt{x^2 + 4}} dx = [ x = \frac{1}{t}, dx = -\frac{1}{t^2}dt,\sqrt{x^2 + 4} = \frac{\sqrt{1 + 4t^2}}{t} ] =\\\\ \ \int -\frac{4t}{\sqrt{1 + 4t^2}} \ dt = [u = 1+4t^2, du = 8tdt, \frac{du}{8t} = dt] = \int -\frac{1}{2\sqrt{u}}du =\\\\ -\sqrt{u} + C = -\sqrt{1 + 4t^2} + C = -\sqrt{1 + \frac{4}{x^2}} + C = -\frac{\sqrt{x^2 + 4}}{x} + C \\ \int \frac{1}{\sqrt{x^2 + 4}} \ dx + \int \frac{4}{x^2\sqrt{x^2 + 4}} \ dx = ln|x + \sqrt{x^2 + 4}| -\frac{\sqrt{x^2 + 4}}{x} + C $$