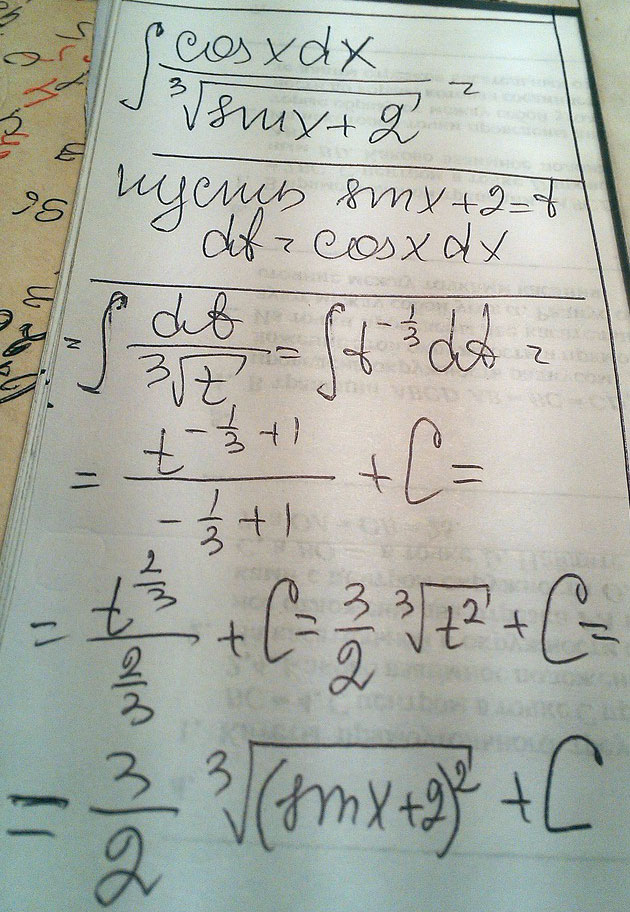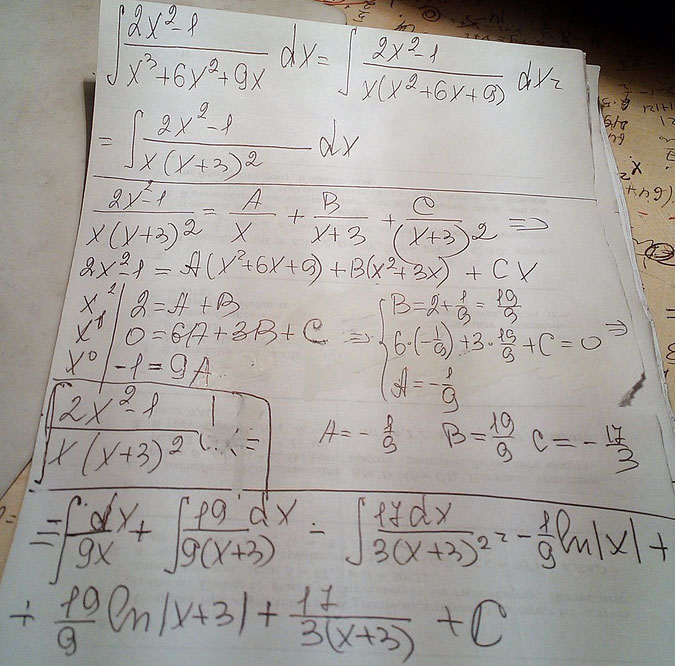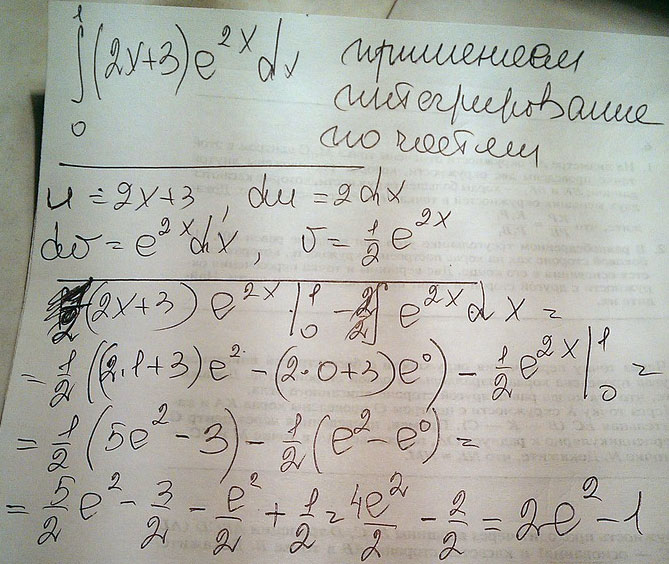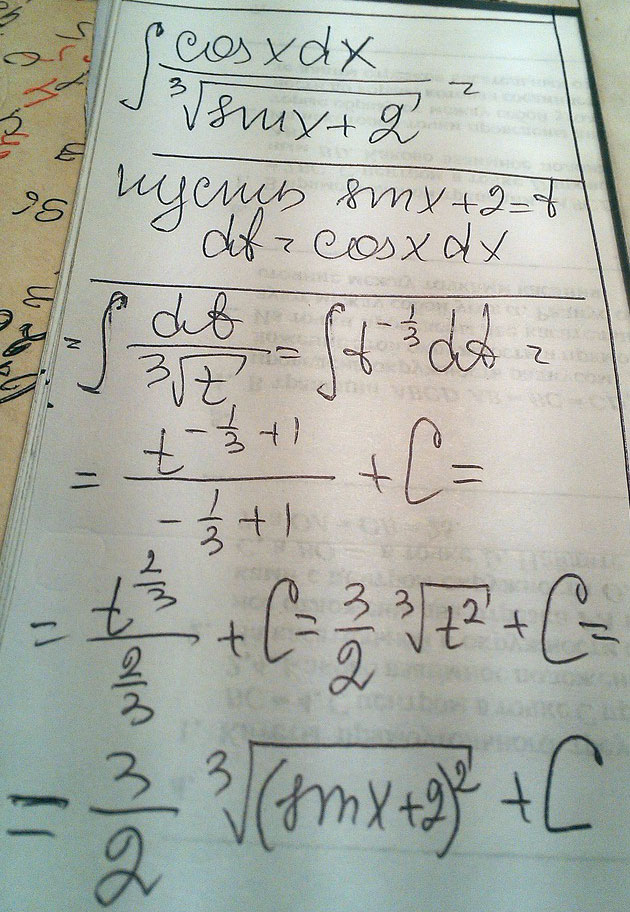интеграл »
найти интеграл - страница 21
Интеграл x^(13)•ln xdx
Решение: Решение
Используем интегрирование по частям: ∫udv = uv − ∫vdu Пусть u(x) = lnx и пусть dv(x) = x¹³ dx.
Затем du(x) = 1/x dx. Чтобы найти v(x):
Интеграл ∫(x^n)dx = x^(n+1) / (n+1):
∫x¹³dx = x¹⁴/14
Теперь решаем под-интеграл.
Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции: ∫( x¹³/14)dx = (1/14)∫x¹³dx
Интеграл ∫(x^n)dx = (^n+)/(n+1): ∫x¹³dx = x¹⁴/14
Таким образом, результат будет: x¹⁴/196
Теперь упростить: (x¹⁴/196)*(14*ln(x) − 1)
Добавляем постоянную интегрирования:
(x¹⁴/196)*(14*lln(x) − 1) + C
Ответ:(x¹⁴/196)*(14*ln(x) − 1) + C
Найти интегралы: \( 1) \int\limits^1_0 {(x^3-5x)} \, dx\\ 2) \int\limits^3_1 {(4x-x^2)} \,dx\\ 3) \int\limits^2_0 {(3x^2+2x-1)} \,dx\\ 4) \int\limits^{\frac{\pi}2}_{\frac{\pi}6} {\frac3{sin^2x}} \, dx \\ 5) \int\limits^3_0 {\frac1{(x-2)^2}} \, dx \)
Решение: $$ 1) \int\limits^1_0 {(x^3-5x)} \, dx =(\frac{x^4}4-\frac{5x^2}{2})|^1_0=(\frac14-\frac52)-0=(0.25-2.5)=-2.25\\ 2) \int\limits^3_1 {(4x-x^2)} \,dx =(\frac{4x^2}2-\frac{x^3}{3})|^3_1=\\=(2x^2-\frac{x^3}{3})|^3_1=(18-9)-(2-\frac13)=9-2+\frac13=7+\frac13=7\frac13\\ 3) \int\limits^2_0 {(3x^2+2x-1)} \,dx =(\frac{3x^3}3-\frac{2x^2}{2}-x)|^2_0=(x^3-x^2-x)|^2_0=\\=(8-4-2)-0=2\\ \\ 4) \int\limits^{\frac{\pi}2}_{\frac{\pi}6} {\frac3{sin^2x}} \, dx =3\int\limits^{\frac{\pi}2}_{\frac{\pi}6} {\frac1{sin^2x}} \, dx =2*(-ctgx)|^{\frac{\pi}2}_{\frac{\pi}6}=-2ctgx|^{\frac{\pi}2}_{\frac{\pi}6}=\\=-2(ctg\frac{\pi}2-ctg\frac{\pi}6)=-2(0-\sqrt3)=-2*(-\sqrt3)=2\sqrt3 \\ 5) \int\limits^3_0 {\frac1{(x-2)^2}} \, dx =\int\limits^3_0 {(x-2)^{-2}} \, dx =\int\limits^{3-2}_{0-2} {t^{-2}} \, dx =\int\limits^{1}_{-2} {t^{-2}} \, dx =\\=\frac{t^{-1}}{-1} |^1_{-2}=-t^{-1}|^{1}_{-2}=-(1^{-1})+(-2)^{-1})=-1-\frac12=-\frac32 $$
Интеграл \( \int {\frac{2x^2 -1}{x^3+6x^2 +9x}} \, dx\)
Решение: $$ \int {\frac{2x^2 -1}{x^3+6x^2 +9x}} \, dx = \int {\frac{2x^2 -1}{x \cdot (x^2+6x +9)}} \, dx = \int {\frac{2x^2 -1}{x \cdot (x+3)^2}} \, dx = (*) \\ \\ \frac{A}{x} + \frac{B}{x+3}+ \frac{C}{(x+3)^2}=\frac{2x^2-1}{x \cdot (x+3)^2} \\ \\ A(x^2 +6x+9) + B(x^2+3x) +Cx=2x^2-1 \\ \left\{\begin{aligned} & A +B=2 \\ & 6A+3B+C=0 \\ & 9A =-1 \end{aligned}\right. \ \ \left\{\begin{aligned} & B = 2+\frac{1}{9}=\frac{19}{9} \\ & C=\frac{6}{9}-\frac{3 \cdot 19}{9}=\frac{2-19}{3}=-\frac{17}{3} \\ & A =\\= -\frac{1}{9}\end{aligned}\right. \\ \\ \\ \int {(-\frac{1}{9x} + \frac{19}{9 \cdot (x+3)} - \frac{17}{3 \cdot (x+3)^2})} \, dx=\\= -\frac{1}{9} \int \frac{dx}{x} + \frac{19}{9} \int \frac{dx}{x+3} - \frac{17}{3} \int \frac{dx}{(x+3)^2}= \\\\ =-\frac{1}{9} \ln{|x|} + \frac{19}{9} \ln{|x+3|} - \frac{17}{3} \cdot (- \frac{1}{x+3}) + C = \\ \\ = -\frac{1}{9} \ln{|x|} + \frac{19}{9} \ln{|x+3|} + \frac{17}{ 3 \cdot (x+3)}+ C $$
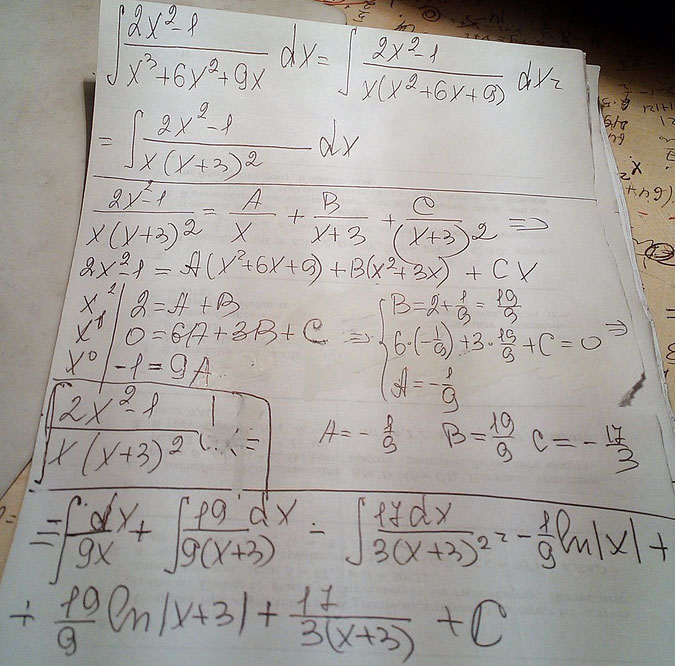
Найти интеграл \(\int\limits_0^1(2x+3)e^{2x}dx \)
Решение: Интегрируем по частям
$$ \int {u} \, dv = uv - \int {v} \, du \\ u=(2x+3); \ \ \ \, du =2\,dx \\ \\ v=e^{2x}; \ \ \, dv= \int\ {e^{2x}} \, dx =\frac{1}{2} e^{2x} \\ ((2x+3)\cdot \frac{1}{2} \cdot e^{2x})|^1_0 - \int \limits^1_0 {\frac{1}{2} \cdot e^{2x} \cdot 2} \, dx = \frac{1}{2} \cdot ((2x+3)\cdot e^{2x})|^1_0 - \int \limits^1_0 { e^{2x}} \, dx = \\ \\ =(\frac{1}{2} \cdot (2x+3)\cdot e^{2x} - \frac{1}{2} \cdot e^{2x} )|^1_0 =\frac{1}{2} \cdot (e^{2x} \cdot (2x+2 )|^1_0= \\ \\ =\frac{1}{2} \cdot (4e^{2} - 2e^0 )=\frac{4e^2-2}{2} = 2e^2-1 $$
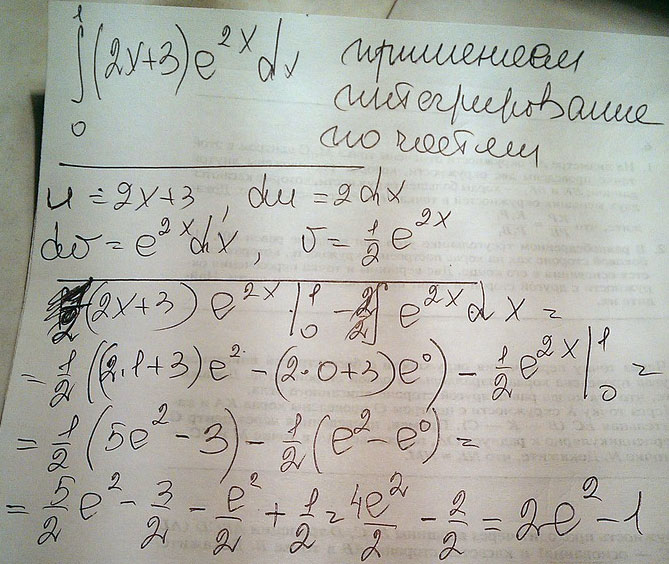
Интеграл \( \int\frac{cosx dx}{\sqrt[3]{sinx+2}}\)
Решение:Замена $$ t = \sin{x}; \ \ dt= \cos{x} \, dx \ \Rightarrow \ dx = \frac{dt}{\cos{x}} \\ \\ \int {\frac{\cos{x}}{ \sqrt[3]{t+2} } \cdot \frac{dt}{\cos{x}}}=\int \frac{dt}{ \sqrt[3]{t+2} }= \int \frac{d(t+2)}{\sqrt[3]{t+2}}=\frac{(t+2)^{\frac{2}{3}}}{\frac{2}{3}} +C =\\ \\ = \frac{3}{2} \cdot \sqrt[3]{(t+2)^2} + C= \frac{3}{2} \cdot \sqrt[3]{(\sin{x}+2)^2} + C $$