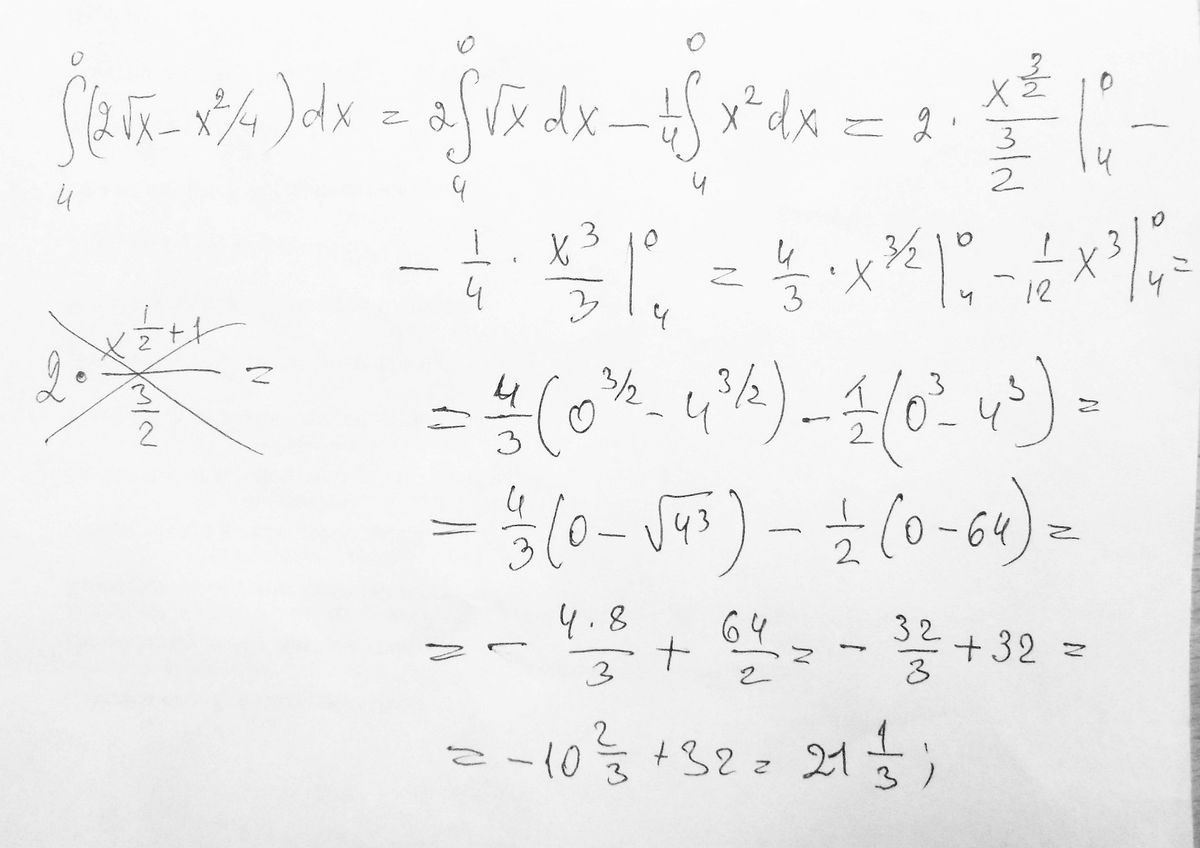интеграл »

найти интеграл - страница 3

  • Найти интеграл dx / sqrt(8+2х-х^2)


    Решение: $$ \displaystyle \int \frac{1}{ \sqrt{8+2x-x^2}}\, dx = \int{ \frac{1}{ \sqrt{8+1-1+2x-x^2}}} \, dx= \\\displaystyle\int { \frac{1}{ \sqrt{9-(x-1)^2}}}\,dx = (x-1=a; dx=da)= \int { \frac{1}{ \sqrt{9-a^2}} } \, da= \\ \displaystyle =\int{ \frac{1}{3 \sqrt{1-a^2/9} }} \, da= \frac{1}{3} \int{ \frac{1}{ \sqrt{1-a^2/9}}} \, da=(a/3=t;1/3da=dt)= \\ \displaystyle= \frac{1}{3} \int{ \frac{1}{1/3 \sqrt{1-t^2}} } \, dt= \int { \frac{1}{ \sqrt{1-t^2}}} \, dt=arcsin(t)+C=(t=a/3)= \\ \displaystyle=arcsin(a/3)+C=(a=x-1)=arcsin \frac{x-1}{3}+C $$

  • S=интеграл от 3 до -3 (х^2+9)dx=(x^3/3 + 9x)=


    Решение: Сначала находим неопределённый интеграл F(x) - это вы сделали верно.

    Потом находим определённый как F(x2)-F(x1), где x2 - верхний, а x1 - нижний пределы интегрирования.

    В верхнем: (3^3/3 + 9*3)=36

    В нижнем: ((-3)^3/3 + 9*(-3))= -36

    Итого: 36 - (-36) = 72

    , если сильно надо, можно проверить графиком

  • чему равен интеграл от 2 до -2 от (4-х^2)dx = ?

    и интеграл от п/4 до 0 от 3cos2x dx = ?


    Решение: $$ \\\int \limits_{-2}^2 4-x^2\, dx=\\ \Big[4x-\frac{x^3}{3}\Big]_{-2}^2=\\ 4\cdot2-\frac{2^3}{3}-(4\cdot(-2)-\frac{(-2)^3}{3})=\\ 8-\frac{8}{3}-(-8+\frac{8}{3})=\\ 16-\frac{16}{3}=\\ \frac{48}{3}-\frac{16}{3}=\\ \frac{32}{3} \\ \\\int \limits_0^{\frac{\pi}{4}}3\cos2x\, dx=\\ 3\int \limits_0^{\frac{\pi}{4}}\cos2x\, dx=(*)\\ t=2x\\ dt=2\, dx\\ dx=\frac{1}{2}dt\\ 3\int \limits_0^{\frac{\pi}{4}}\cos t\cdot\frac{1}{2}dt=\\ \frac{3}{2}\int \limits_0^{\frac{\pi}{4}}\cos t\, dt=\\ \frac{3}{2}\Big[\sin t\Big]_0^{\frac{\pi}{4}}\\ (*)=\frac{3}{2}\Big[\sin 2x\Big]_0^{\frac{\pi}{4}}=\\ \frac{3}{2}(\sin (2\cdot\frac{\pi}{4})-(\sin (2\cdot0)))=\\ \frac{3}{2}(\sin (\frac{\pi}{2})-(\sin 0))=\\ \frac{3}{2}(1-0)=\\ \frac{3}{2} $$

  • Интеграл от 4 до 0 (2√х - х²/4)dx.


    Решение: Разность интегралов
    $$ \int\limits^0_4 { 2\sqrt{x}} \, dx - 1/4* \int\limits^0_4 { x^{2}} \, dx = 2* (x^{3/2} /(3/2) ) | - 1/4* x^{3}/ 3) | $$ = 
    1/12 вместо 1/2
    окончательно
    - 32/3 + 64/12 = - 128/12 + 64/12 = - 64/12 = - 16/3

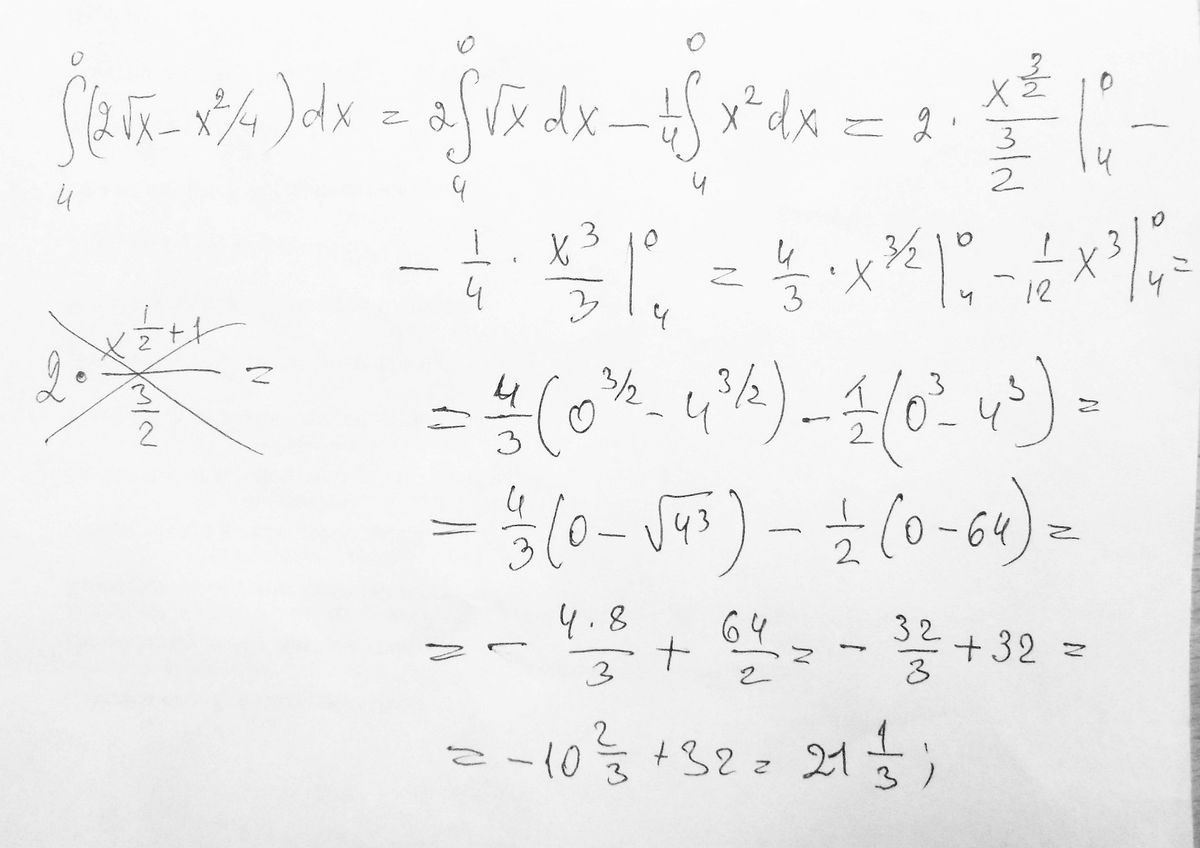
    Разность интегралов int limits sqrt x dx - int limits x dx x - x   вместо окончательно- - - -...

  • Найти интеграл
    \( \int\limits \)(2\( x^{3} \)+х-5)dx


    Решение: $$ \int\limits {2}{x^{3}}dx = 2 \int\limits x^{3} \\dx = 2 * (x^{4})/4 =\\ = (x^{4})/2 \\ \int\limits {xdx} = (x^{2})/2 \\ \int\limits{-5dx} = -5 \int\limits{ dx }= -5x$$
    -
    Відповідь: $$ (x^{4} + x^{2})/2 - 5x $$

<< < 123 4 5 > >>