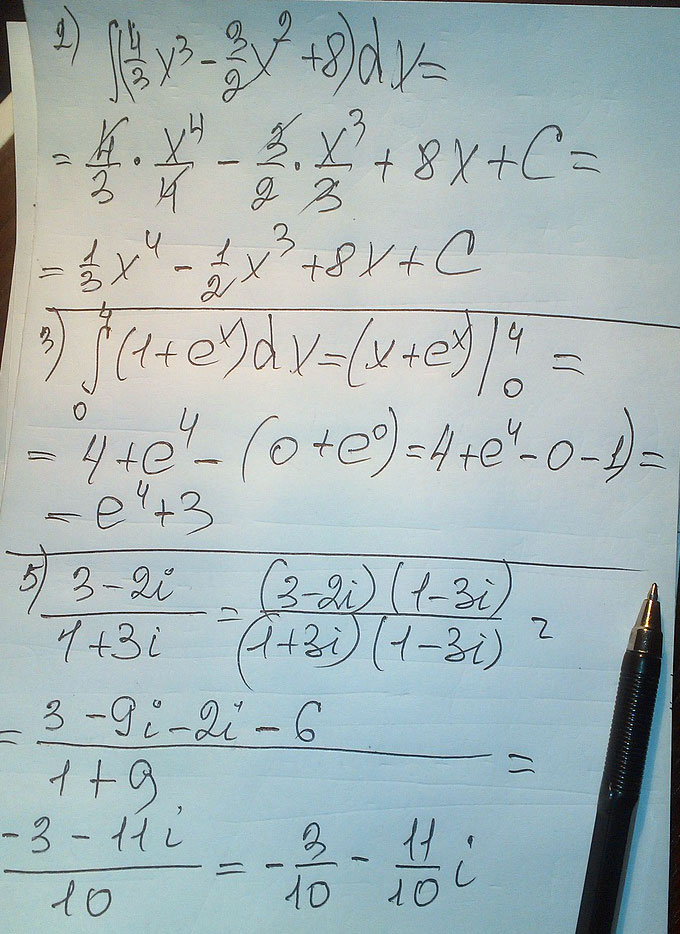найти интеграл - страница 4
1. Какая из функций является первоначальной для функции ∫(х)=3х²
2. Найдите для функции f(х) = 8х³, первоначальную, график которой проходит через точку А (1, 2).
3. Вычислите интеграл \( \int\limits^0_ 1 ({x} +1)\, dx \)
Решение: 1) Для этого находим интеграл функции
Y 3x²
∫3x²dx = x³ + С - ОТВЕТ
2) Находим интеграл функции
Y = 8x³
Z = ∫8x3dx = 1/4*8*x⁴ + С = 2*x⁴ +С
Чтобы найти значение С подставим значения координат точки А(1;2) = Х=1 Z=2
Z = Ay = 2 = 2*1⁴ + C или С = 0
Z= 2*x⁴ - ОТВЕТ
3) Вычислить интеграл функции
Y = ∫(x+1)dx = 1/2*x² + x + С
Y(0) = 0
Y(1) = 3/2 -
Как написано = от 1 до 0, то ОТВЕТ : -3/2
Решите ИНТЕГРАЛЫ \( \int\dfrac{\sqrt[3]{\arctan x}}{1+x^2}dx\\ \int \tan 3x\,dx\\ \int\cos^8x\sin x\,dx\\ \int\dfrac{x}{(x-2)(x^2+6x+8)}dx\\ \int(3-x)\sin x\,dx\\ \int\dfrac{dx}{\sin^2\frac x6}\\ \int\dfrac{x^2+1}{(x-1)^3(x+3)}dx\\ \int \dfrac{3x+4}{\sqrt{-x^2+6x-8}}\,dx\\ \int \arcsin\dfrac x2\,dx \)
Решение: Везде опускаю константу интегрирования.$$ \int\dfrac{\sqrt[3]{\arctan x}}{1+x^2}dx=\int t^{1/3}dt=\dfrac{3t^{4/3}}4 $$
(замена t=atctg x)
$$ \int \tan 3x\,dx=-\dfrac13\ln|\cos3x| \\ \int\cos^8x\sin x\,dx=-\int t^8\,dt=\dfrac{t^9}9 $$
t=cos x
$$ \int\dfrac{x}{(x-2)(x^2+6x+8)}dx=\int\left(\dfrac{1/4}{x-2}-\dfrac{1/3}{x+4}+\dfrac{1/12}{x-2}\right)\,dx=\\=\dfrac14\ln|x-2|-\dfrac13\ln|x+4|+\dfrac1{12}\ln|x-2| \\ \int(3-x)\sin x\,dx=-3\cos x+x\cos x-\int\cos x\,dx=(x-3)\cos x\\-\sin x \\ \int\dfrac{dx}{\sin^2\frac x6}=-6\cot \dfrac x6 \\ \int\dfrac{x^2+1}{(x-1)^3(x+3)}dx=\int\left(\dfrac{-5/32}{x+3}+\dfrac{5/32}{x-1}+\dfrac{3/8}{(x-1)^2}\right.+\\+\left.\dfrac{1/2}{(x-1)^3}\right)\,dx=-\dfrac5{32}\ln|x+3|+\dfrac5{32}\ln|x-1|-\dfrac{3/8}{x-1}-\\-\dfrac{1/4}{(x-1)^2} \\ \int \dfrac{3x+4}{\sqrt{-x^2+6x-8}}\,dx=\int\dfrac{-\frac32(-2x+6)+13}{\sqrt{-x^2+6x-8}}\,dx=\\=-3\sqrt{-x^2+6x-8}+13\int\dfrac{dx}{\sqrt{-x^2+6x-8}}=-3\sqrt{-x^2+6x-8}\\+13\int\dfrac{dx}{\sqrt{1-(x-3)^3}}=-3\sqrt{\dots}+13\arcsin(x-3) \\ \int \arcsin\dfrac x2\,dx=x\arcsin\dfrac x2-\int\dfrac{x}{\sqrt{4-x^2}}\,dx=x\arcsin\dfrac x2+\\+\sqrt{4-x^2} $$
Найти производные, используя правила вычисления производных \(1)\; y=-\frac{1}{7}x^3-2cosx+11,3\\2)\; y=\sqrt3sinx\cdot \sqrt[4]{x}\\ 3)\; y=cos^3x+3sin^2x\\ \)
Найти неопределенные интегралы \( \int (2-13x^7-2\sqrt[4]{x^7}+\frac{1}{x^3})dx\\ \int arcsinx\, dx=[\, u=arcsinx\;,\; du\\ \)
Решение: $$ 1)\; y=-\frac{1}{7}x^3-2cosx+11,3\\\\y’=-\frac{3}{7}x^2+2sinx\\\\2)\; y=\sqrt3sinx\cdot \sqrt[4]{x}\\\\y’=\sqrt3cosx\cdot \sqrt[4]{x}+\sqrt3sinx\cdot \frac{1}{4}\cdot x^{-\frac{3}{4}}\\\\3)\; y=cos^3x+3sin^2x\\\\y’=3cos^2x\cdot (-sinx)+6sinx\cdot cosx=-3cos^2x\dot sinx+3sin2x\\\\4)\int (2-13x^7-2\sqrt[4]{x^7}+\frac{1}{x^3})dx=2x-13\cdot \frac{x^8}{89}-2\cdot \frac{x^{\frac{11}{4}}\cdot 4}{11}+\frac{x^{-2}}{-2}+C \\ \int arcsinx\, dx=[\, u=arcsinx\;,\; du=\frac{dx}{\sqrt{1-x^2}}\;,\; dv=dx,\; v=x\, ]=\\\\=x\cdot arcsinx-\int \frac{x\, dx}{\sqrt{1-x^2}}=x\cdot arcsinx+\frac{1}{2}\cdot 2\sqrt{1-x^2}+C $$Интегралы решить: \( \int\limits {( \frac{4x^{3}}{3}- \frac{3x^{2}}{2}+8)}\\ \int\limits^4_0 {(1+e^{x})}\)
\( \frac{3-2i}{1+3i} \)
Решение:2) $$ \int\limits {( \frac{4x^{3}}{3}- \frac{3x^{2}}{2}+8)} \, dx=\frac{4x^{4}}{4*3}-\frac{3x^{3}}{3*2}+8x+C=\frac{x^{4}}{3}-\frac{x^{3}}{2}+8x+C $$
4) $$ \int\limits^4_0 {(1+e^{x})} \, dx=x+e^{x}|^{4}_{0}=4+e^{4}-0-e^{0}=4+e^{4}-1=3+e^{4} $$
5) $$ \frac{3-2i}{1+3i}= \frac{(3-2i)*(1-3i)}{(1+3i)(1-3i)}=\frac{3-9i-2i+6i^{2}}{1-9i^{2}}= \ =\frac{-3-11i}{1+9}=-\frac{3+11i}{10}=-0.3-1.1*i $$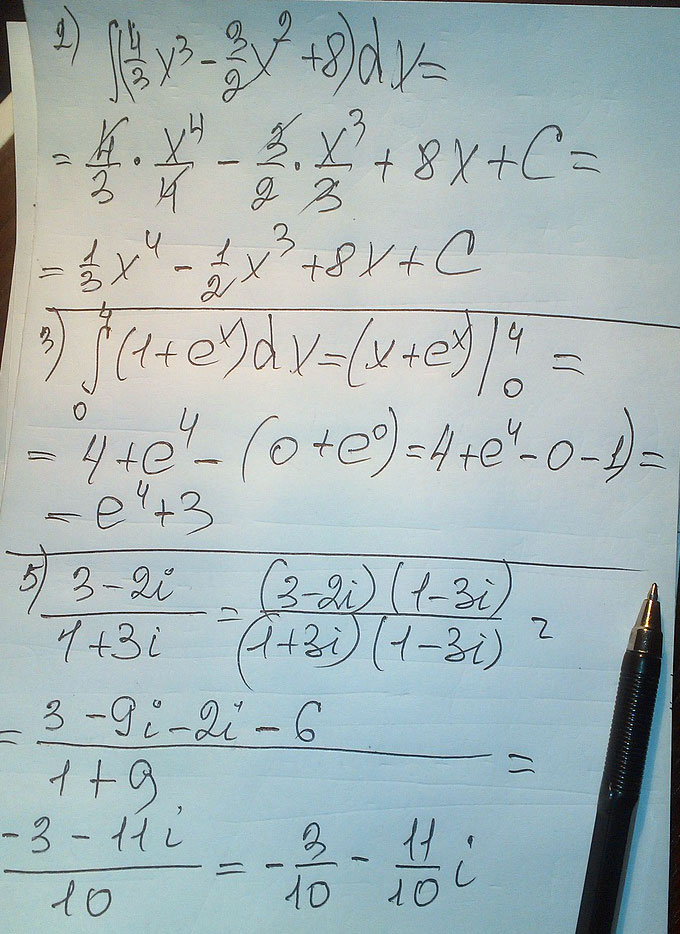
Решите уравнение:
2) х знак интеграла 1 (1-4t) dt = 12 - 9x;
4) -2 знак интеграла x (5t +1)dt = 6+x.
Решение: 0. Непонятно, относительно какой переменной решать уравнения. Предположу, что относительно х.
1. Непонятно условие, что за 1 под знаком интеграла?
2. Так как интегрирование идёт по t, х под знаком интеграла - обычная константа, поэтому, проинтегрировав по t, получим
-2*x*(5*t*t/2 + t) = 6+x
Это линейное уравнение относительно х.
x*(1 +2*t + 5*t*t) = -6
x = -6/(5*t*t + 2*t + 1)
это и есть ответ.
Осталось слегка поисследовать его. Знаменатель не может быть равным 0, попробуем найти, когда это происходит и происходит ли вообще.
Найдём дискриминант квадратного трехчлена знаменателя
D = 4-4*5*1<0
Уравнение в области действительных чисел не имеет решений, а значит и знаменатель никогда в 0 не обратится.