интеграл »

найти интеграл - страница 6

  • Интеграл(sinx/cos^3x)dx


    Решение: Отделим один косинус в знаменателе и представим выражение в виде тангенса
    Используем в процессе решение табличные формулы и подведение под знак дифференциала
     $$ \int {x^n} \, dx=\frac{x^{n+1}}{n+1} +C; \ \ (tgx)’=\frac{1}{cos^2{x}} \\ \int {\frac{\sin{x}}{\cos{x} \cdot \cos^2{x}}} \, dx = \int {\frac{tgx}{\cos^2{x}}} \, dx = \int {tgx} \, d(tgx)=\frac{tg^2x}{2} +C $$

  • Определенный интеграл. ∫ сверху2 внизах0 (3x^2-2x+4)dx с подробным решением


    Решение: Берем по-очереди первообразную от каждого слагаемого
    потом подставляем вместо Х верхний предел, отнимаем нижний и готово!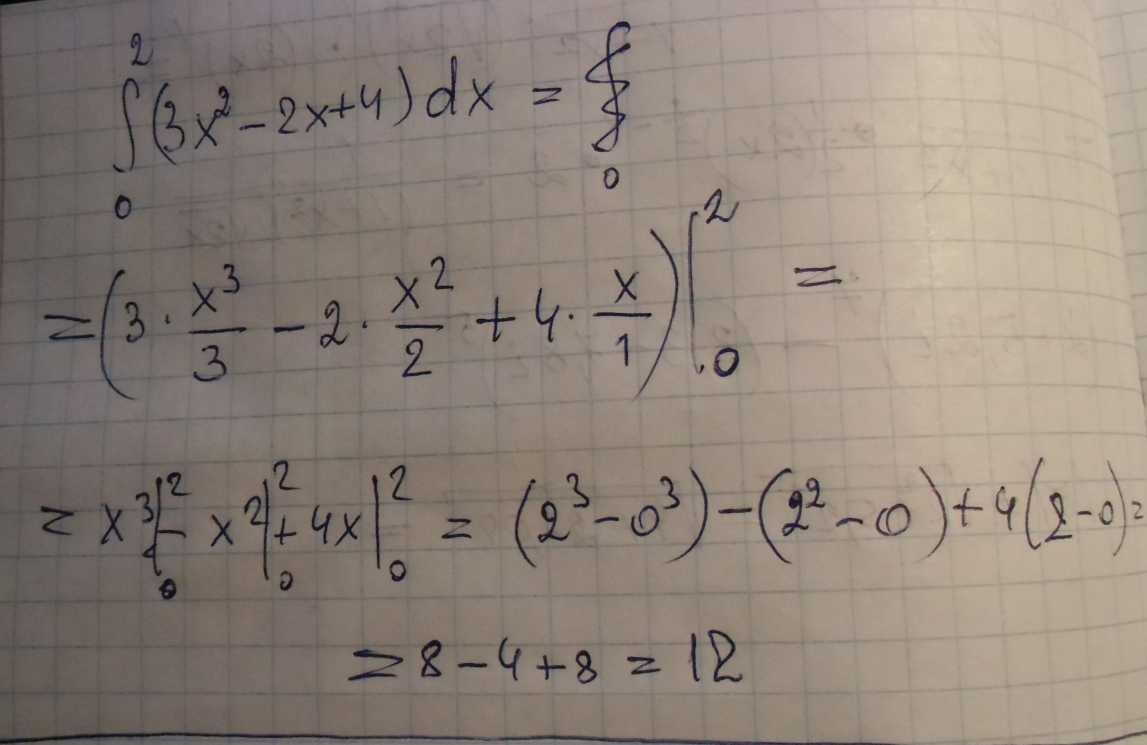 Берем по-очереди первообразную от каждого слагаемогопотом подставляем вместо Х верхний предел отнимаем нижний и готово...



  • 1) lg(2x-5)>log(5x+14) 2) интеграл (5x^4-3x^2+3)dx 3) объем цилиндра, если диаметр 10, а образующая 12 4) сколькими способами можно расставить 9 книг в библиотеке 5) вектор a (2;-4;10) вектор b (3;-2;-4) найти 2a-4b


    Решение: вы имели виду что справа тоже lg

    1) 2x-5>5x+14

      -19>3x

      x<-19/3

      2x-5>0

    2) (5x^4-3x^2+3 )dx= x^5-x^3+3x + C 

    3) V=S*H

      S=piR^2

      D=2R

      R=10/2=5

      L=H

      S=25 * pi

      V=25*pi*12=300pi

    4) по сколько ?

      если просто то 9!=1*2*3*4*5*6*7*8*9

    5) 2a=(4;-8;20)

      4b=(12;-8;-16)

      2a-4b= (4-12) ; (-8+8) ; (20+16) = (-8 ; 0 ; 36)

     

  • Интеграл sin(π/4-4x)dx
    Интеграл √8x-9 dx
    Интеграл dx/(5-3x)⁴
    )
    )


    Решение: $$ \int\limits {sin( \frac{ \pi }{4}-4x )} \, dx =- \frac{1}{4} *(-cos( \frac{ \pi }{4}-4x ))+C= \frac{1}{4}cos( \frac{ \pi }{4} -4x) +C \\ \int\limits { \frac{1}{(5-3x) ^{4} } } \, dx = \int\limits { (5-3x)^{-4} } \, dx= \frac{(5-3x) ^{-4+1} }{-3*(-4+1)} +C= \frac{ (5-3x)^{-3} }{9} +C= \ =\frac{1}{9* (5-3x)^{3} } +C \\ \int\limits { \sqrt{8x-9} } \, dx = \int\limits {(8x-9) ^ \frac{1}{2} } \, dx = \frac{(8x-9) ^{ \frac{1}{2}+1 } }{8*( \frac{1}{2}+1 )} +C= \frac{(8x-9)* \sqrt{8x-9} }{12} +C $$

  • Интеграл (x+4)/((x^3)-(x^2)-2x) dx


    Решение: X^3 - x^2 - 2x = x(x^2 - x - 2) = x(x + 1)(x - 2)
    Все корни простые, тогда проще всего разложить дробь из подынтегрального выражения на простейшие (простите за три однокоренных слова в одном предложении).
    f(x) = (x + 4) / x(x + 1)(x - 2) = A/x + B/(x + 1) + C/(x - 2)
    Определим сначала, например, A. Домножим всё на x:
    x f(x) = A + xB/(x + 1) + xC/(x - 2)
    Подставляя x = 0, находим
    A = 4/(1 * (-2)) = -2 (надо всего лите "закрыть пальцем" множитель x и подставить в то, что осталось, x = 0)
    Аналогично "методом пальца" получаем
    B = 3/((-1) * (-3)) = 1
    C = 6/(2 * 3) = 1
    Итак, f(x) = -2/x + 1/(x + 1) + 1/(x - 2). Теперь интеграл легко берется, ответ
    C - 2ln|x| + ln|x + 1| + ln|x - 2|

<< < 456 7 8 > >>