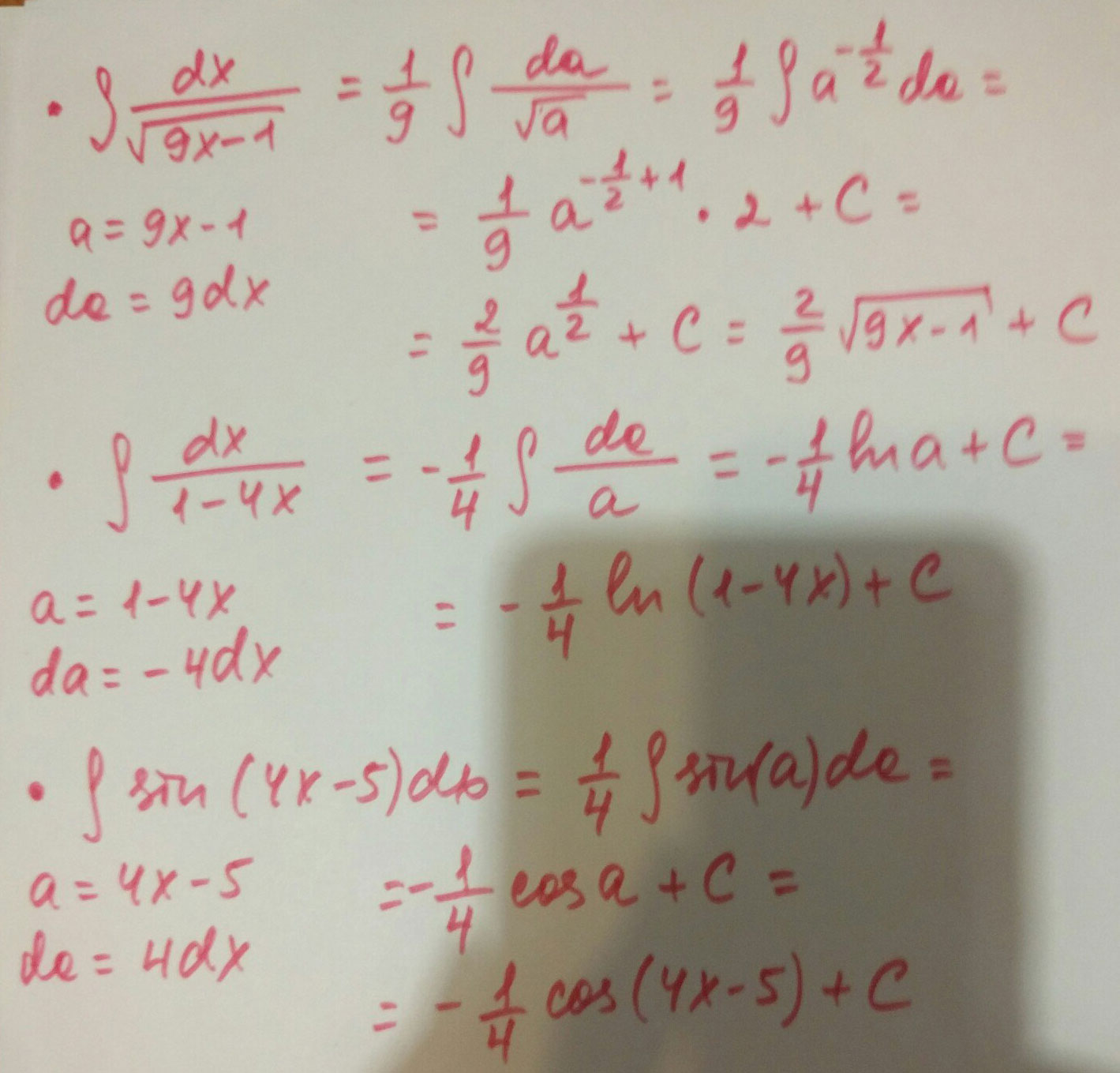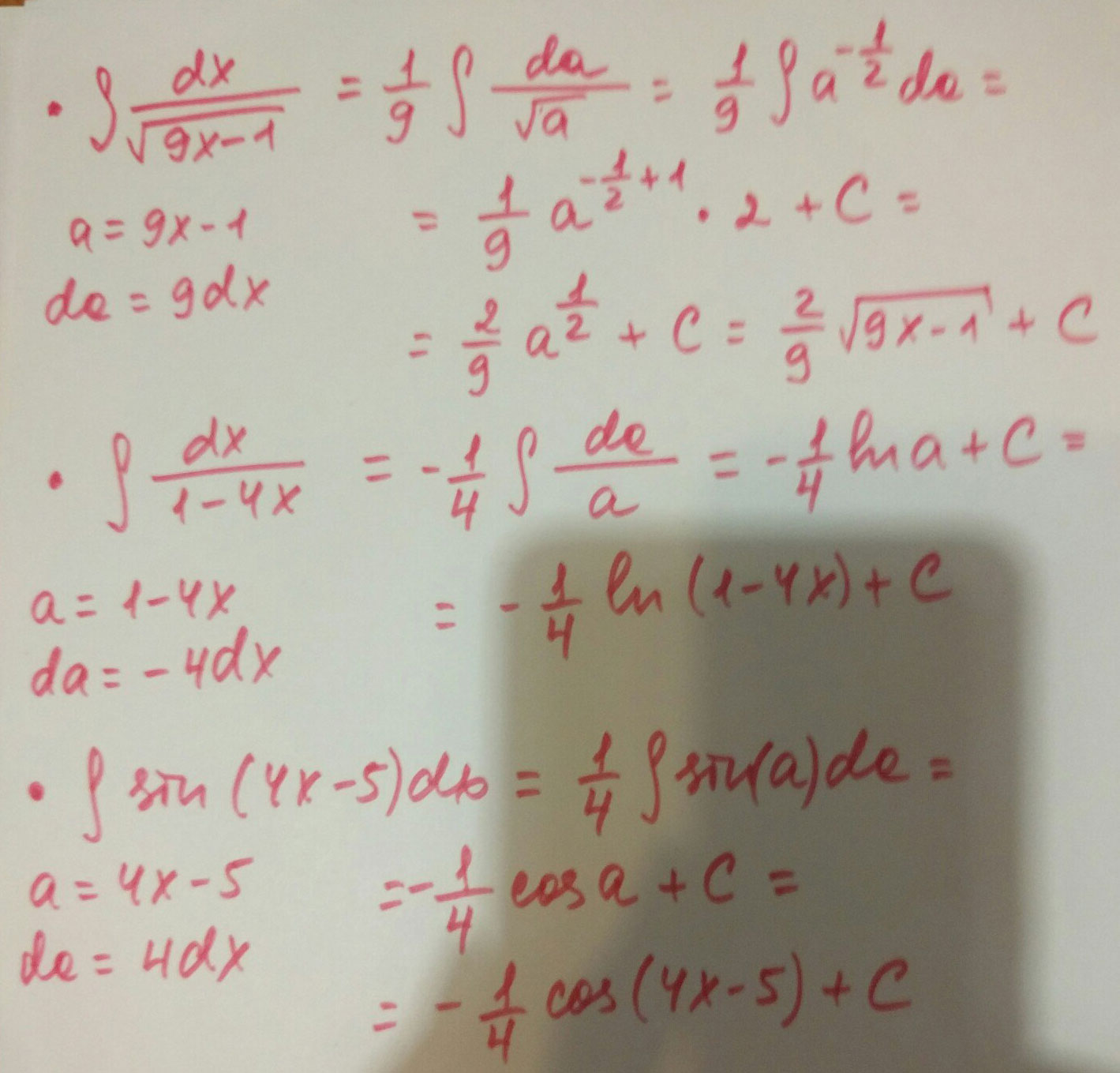интеграл »
найти интеграл - страница 8
Интеграл (x^2*dx)/(x^3+8)
Решение: Решение подстановкой в аргумент.
Определяем функцию:
$$ \alpha(x)=x^3+8\\ \frac{d\alpha}{dx}=3x^2\Rightarrow d\alpha=3x^2dx $$
Подставляем в интеграл:
$$ \int \frac{x^2}{x^3+8}dx=\frac{1}{3}\int\frac{3x^2dx}{x^3+8}=\frac{1}{3}\int\frac{d\alpha}{\alpha} $$
Получили мгновенный интеграл по $$ \alpha $$.
Решаем: $$ \int\frac{d\alpha}{\alpha}=\ln|\alpha| $$
Подставляем обратно как функцию $$ x $$:
$$ \ln|\alpha|=\ln|x^3+8| $$
Ответ: $$ \int\frac{x^2}{x^3+8}dx=\frac{1}{3}\ln|x^3+8|+\mathbf{C} $$РЕШИТЕ 2X³-∛X +3√X dx
5x² НЕОПРЕДЕЛЕНЫЙ ИНТЕГРАЛ
Решение: ∫ (2X³-∛X +3√X ) / 5x² = ∫ 2X³/5x² dx -∫ ∛X/5x² dx +∫ 3√X/5x² dx =
= 2/5 ∫ X³/x² dx - 1/5 ∫ ∛X/x² dx + 3/5 ∫√X/x² dx =
=2/5 ∫ X dx - 1/5 ∫ ∛X/x² dx + 3/5 ∫√X/x² dx =
= 1/5 x^2 + 3/10 ∛x/x - 6/5 *1/√x =
= x^2/5 + 3∛x/10x - 6/5√x
$$ \int\limits { \frac{2x^3- \sqrt[3]{x}+3 \sqrt{x} }{5x^2} } \, dx = \int\limits \frac{2x^3}{5x^2}dx -\int\limits \frac{ \sqrt[3]{x} }{5x^2}dx+\int\limits \frac{3 \sqrt{x} }{5x^2}dx = \\ \\ = \int\limits \frac{2}{5}xdx-\int\limits \frac{1}{5}x^{- \frac{5}{3} }dx+\int\limits \frac{3}{5}x^{- \frac{3}{2} }dx= \frac{x^2}{5} + \frac{3 \sqrt[3]{x} }{10x}- \frac{6 \sqrt{x} }{5x} = \\ \\ = \frac{2x^3+3 \sqrt[3]{x}- 12 \sqrt{x} }{10x} $$
Решите : \( \int\limits^ 0_4 { \frac{dx}{ x^{2} +3 x -4} } \, \)
только интеграл от -4, до 0
Решение: Разложим эту дробь на простейшие.
$$ \frac{1}{x^2+3x-4}=\frac{1}{(x+4)(x-1)}=\frac{A}{x+4}+\frac{B}{x-1}=\frac{A(x-1)+B(x+4)}{(x+4)(x-1)}\\1=A(x-1)+B(x+4)\\\\x=1:\ \ \ \ \ 1=A*0+B*5\Rightarrow B=\frac{1}{5}\\x=-4:\ \ \ 1=A*(-5)+B*0\Rightarrow A=-\frac{1}{5}\\\frac{1}{x^2+3x-4}=\frac{-\frac{1}{5}}{x+4}+\frac{\frac{1}{5}}{x-1}=\frac{1}{5(x-1)}-\frac{1}{5(x+4)}\\\\\int\limits_{-4}^0\frac{dx}{x^2+3x-4}=\int\limits_{-4}^0(\frac{1}{5(x-1)}-\frac{1}{5(x+4)})dx=\frac{1}{5}*(ln|x-1|-ln|x+4|)|^0_{-4}= \\ =\frac{1}{5}*(ln1-ln4-(ln5-ln0))=\frac{1}{5}*(0-ln20+(-\infty))=-\infty $$1. Тело движется прямолинейно со скоростью \( v(t)= t^{3} +t \) м/с Найдите путь, пройденный телом за промежуток времени от 1с до 2с
2. Вычислите интегралы:
1. \( \int\limits^2_1 {(/x/+/x-3/)} \, dx \)
2. интеграл от -2 до -1 \( \frac{dx}{(5x+11)^{3} } \)
3. интеграл от -2 до -1 \( (/x/+/x-3/dx) \)
3. Используя геометрический смысл интеграла, вычислите: интеграл от -4 до 4 \( \sqrt{64- x^{2} } \)
Решение: Первообразная от пути есть ПУТЬ.
$$ S= \int\limits^2_1 {(t^3+t)} \, dx= \frac{t^4}{4} + \frac{t^2}{2} |^2_1=5,25 $$ м
Ответ: 5,25 м.
$$ \int\limits^2_1 {(|x|+|x-3|)} \, dx =3 \\ \int\limits^{-1}_{-2} { \frac{1}{(5x+11)^3} } \, dx =- \frac{1}{10(5x+11)^2} |^{-1}_{-2}= \frac{7}{72} \\ \int\limits^{-1}_{-2} {(|x|+|x-3|)} \, dx =6 \\ \int\limits^4_{-4} { \sqrt{64-x^2} } \, dx = \frac{1}{2} x\sqrt{64-x^2} +32\arcsin \frac{x}{8} |^4_{-4}=16 \sqrt{3} + \frac{32 \pi }{3} $$
Найти интеграл \( \int\limits \frac{dx}{ \sqrt{9x-1} } \\ \int\limits \frac{dx}{1-4x} \\ \int\limits sin (4x-5)dx\\ \)
Решение: