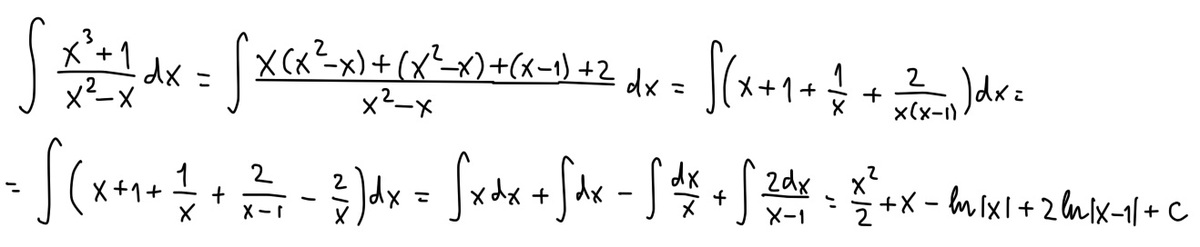интеграл »
найти интеграл - страница 5
Интеграл (x^3+2x^2+4x+3)/x+1 по dx
Решение: $$ \int\limits { \frac{x^3+2x^2+4x+3}{x+1} } \, dx = $$
x³+2x²+4x+3 | x+1
- x³+x² -
- x²+x+3
x²+4x
-x²+x
-
3x+3
- 3x+3
-
0
(x³+2x²+4x+3):(x+1)=x²+x+3
$$ \int\limits{ \frac{x^3+2x^2+4x+3}{x+1} } \, dx= \int\limits{(x^2+x+3} )\, dx= \frac{x^3}{3}+ \frac{x^2}{2}+3x+C $$
Интеграл x^9dx/3x^20+2
Решение: X^9 вносим под дифференциал, как x^10/10, затем делаем замену x^10 = y, получаем:
1/10 * S 1/(3y^2 + 2) dy
теперь выносим из-под знаменателя тройку, чтобы получить табличный интеграл:
1/30 * S 1/(y^2 + 2/3) dy = 1/(30* sqrt(2/3)) * arctg( y/sqrt(2/3)) + c, вместо у подставляем х^10
$$ \int {\frac{ x^{9} }{3 x^{20}+2}} \, dx= \frac{1}{3} \int { \frac{ x^{9} }{ (x^{10}) ^{2} + \frac{2}{3} }} \, dx=[u= x^{10} ;du=10 x^{9}dx; x^{9}dx= \frac{du}{10}]= \\ =\frac{1}{3} \int { \frac{du}{ 10(u ^{2} + \frac{2}{3})} }= \frac{1}{30}\cdot \frac{1}{ \sqrt{ \frac{2}{3} }} arctg \frac{u}{ \sqrt{ \frac{2}{3} } }+C= \frac{1}{30}\cdot \frac{ \sqrt{3} }{ \sqrt{2 } } arctg \frac{x ^{10} \sqrt{3} }{ \sqrt{ 2 } }+C = \\ =\frac{1}{10 \sqrt{6} } arctg \frac{x ^{10} \sqrt{3} }{ \sqrt{ 2 } }+C $$
Решите интеграл: x^3+1 / x^2-x
Решение: Решение на картинке.$$ \int\limits { \frac{x^3+1}{x^2-x} } \, dx = \int\limits {(1+x+ \frac{x+1}{x^2-x}) } \, dx = \int\limits {(x+1+ \frac{2}{x-1}- \frac{1}{x} ) } \, dx =\\=2\ln|x-1|+x-\ln|x|+ \frac{x^2}{2}+C $$
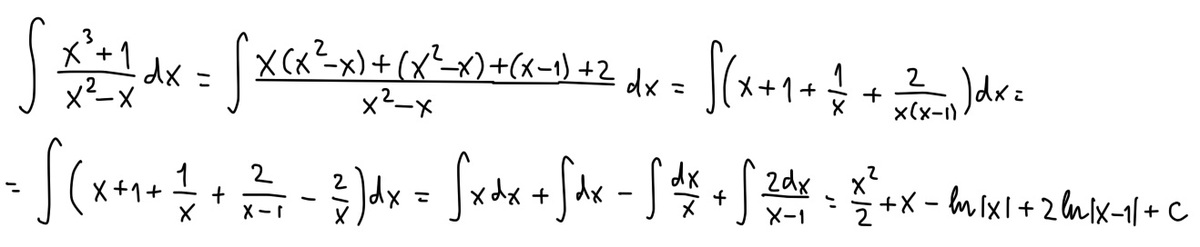
Найти
интеграл dx/3+tg x
Решение: ∫ dx/(3+tgx) =
Подстановка: t = tgx, dt=dx/(cos²x) = (tg²x+1)dx, dx = dt/(t²+1)
х= arctgt
=∫ dt / ((t²+1)*(3+t)=
Преобразование:
1/((t²+1)*(3+t)) = (0,3 - 0,1*t) /(t² +1) +0,1/(3+t)
= 0,3 ∫ dt/(t²+1)dt - 0,05 ∫ d(t²)/ (t²+1) +0,1 ∫ (3+t)dt
а дальше - расписать табличные интегралы и вернуться к Х
Найти интеграл а) sin 3x*cos 3x*dx б) arctg(4x)dx
Решение: А)Int(3/[sin(3x)]^2-cos(2x)) dx = Int 3/[sin(3x)]^2 dx - Int cos(2x) dx =
Int d(3x)/[sin(3x)]^2 - 0.5*Int cos(2x) d(2x) = -ctg(3x) -0.5*sin(2x) + C.
-ctg(-3*pi/2)-0.5*sin(-2*pi/2)+C=3
0 0 C=3
Answer: -ctg(3x) -0.5*sin(2x)+3
Б)2Pin, n прин. Z x = +-(Pi - arccos(1/3)) + 2Pin, n прин. Z 3) sqrt(3) * cosx = sinx |:cosx tgx = sqrt(3) x = arctg(sqrt(3)) + Pik, k прин. Z x = Pi/3 + Pik, k прин