НОД и НОК »

наибольший общий делитель равен наименьшему общему кратному - страница 2

  • НАИБОЛЬШЕЕ ОБЩЕЕ КРАТНОЕ (12 10)
    НАИБОЛЬШЕЕ ОБЩЕЕ КРАТНОЕ (42 56)


    Решение: НОК (12; 10) = 2 * 2 * 3 * 5 = 60 - наименьшее общее кратное
    12 = 2 * 2 * 3 60 : 12 = 5
    10 = 2 * 5 60 : 5 = 12
    НОК (42; 56) = 2 * 2 * 2 * 3 * 7 = 168 - наименьшее общее кратное
    42 = 2 * 3 * 7 168 : 42 = 4
    56 = 2 * 2 * 2 * 7 168 : 56 = 3
    Чтобы найти НОК (наименьшее общее кратное), нужно разложить данные числа на простые множители и найти произведение всех простых множителей, взятых с наибольшим показателем степени.

  • разложить на простые множители числа 120 и 180 и найдите их наибольший общий делитель


    Решение: Для 120                           Для 180
    120|2                                 180|2
    60  |2                                 90  | 2
    30  |2                                 45 | 3
    15  |3                                  15 | 3
    5 |5                                    5|5
    1                                          1
    120=2x2x2x2x3x5                 180=2x2x3x3x5
      НОД= 2 во второй степени x 3 x 5= 60
     

  • Найти Нок и Нод (наименьший общий делитель и наибольший)
    50 и 49
    120, 180 и 200;
    11475 и 19125
    5 класс
    Из 156 чайных, 234 белых и 390 красных роз сделали букеты, причём во всех букетах роз каждого вида было поровну и число таких букетов было больше 50. Сколько букетов сделали из этих роз и сколько роз каждого вида было в одном букете?
    3. В киоск привезли тетради. Если их разложить в пачки по 15 тетрадей в каждую или по 20 тетрадей, то в обоих случаях лишних тетрадей не окажется. Сколько тетрадей привезли в киоск, если их было больше 900, но меньше 1000?


    Решение: 50 и 49 взаимно простые у них один нод=1
    120=2*2*2*3*5
    180=2*2*3*3*5
    200=2*2*2*5*5
    нод(120,180,200)=2*2*5=20
    11475=3*3*3*5*5*17
    19125=3*3*5*5*5*17
    нод(11475,19125)=3*3*5*5*17=3825
    156=2*2*3*13
    234=2*3*3*13
    390=2*3*5*13
    2*3*13=78букетов
    156:78=2=чайные
    234:78=3 белые
    390:78=5красные
    нок=60
    60:15=4
    60:20=3
    привезли 60 тет,120,180 и. т д

  • Как найти наибольший и наименьший общий делитель?


    Решение: 1.(15,9)=3 2. I15,9I=45
    15=3*5
    9=3*3
    1. 3
    2. 3*3*5

    Чтобы найти НОД двух или более натуральных чисел нужно:
    Подчёркиваем одинаковые простые множители в обоих числах. 
    28 = 2 • 2 • 7 
    64 = 2 • 2 • 2 • 2 • 2 • 2Находим произведение одинаковых простых множителей и записать ответ; 
    НОД (28; 64) = 2 • 2 = 4 
    Ответ: НОД (28; 64) = 4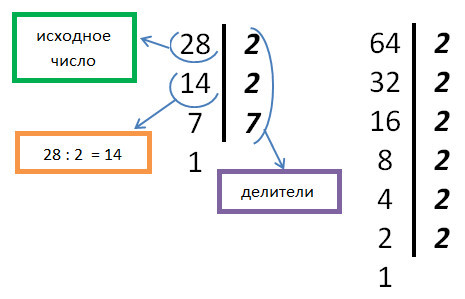

    . . I I . . Чтобы найти НОД двух или более натуральных чисел нужно Подч ркиваем одинаковые простые множители в обоих числах.                    Находим произведение одинаковы...

  • Найди Наибольший общий делитель (a,b), если:
    А) а=2*3*3*5*7; Б) а=7*13*17;
    b=2*2*3*7*11; b=2*5*13;
    В) а=2*2*2*3*3*5*7; Г) а = 2*2*5*7 ;
    b=2*2*3*7*11 b = 2*5*7;

    Д) а = 2*2*2*3*3*5*7; Е) а = 2*2*3*3*5;
    b = 2*2*3*5; b=2*2*3*3*7.


    Решение: А) а=2*3*3*5*7 а=630
    b=2*2*3*7*11 b=924
    НОД(а,b)=42
    Б) а=7*13*17 а=1547
    b=2*5*13 b=130
    НОД(а,b)=13
    В) а=2*2*2*3*5*7 а=840
    b=2*2*3*7*11 b=924
    НОД(а,b)=84
    Г) а=2*2*5*7 а=140
    b=2*5*7 b=70
    НОД(а,b)=70
    Д) а=2*2*2*3*3*5*7 а=2520
    b=2*2*3*5 b=60
    НОД(а,b)=60
    Е) а=2*2*3*3*5 а=180
    b=2*2*3*3*7 b=252
    НОД(а,b)=36

<< < 12 3 4 > >>