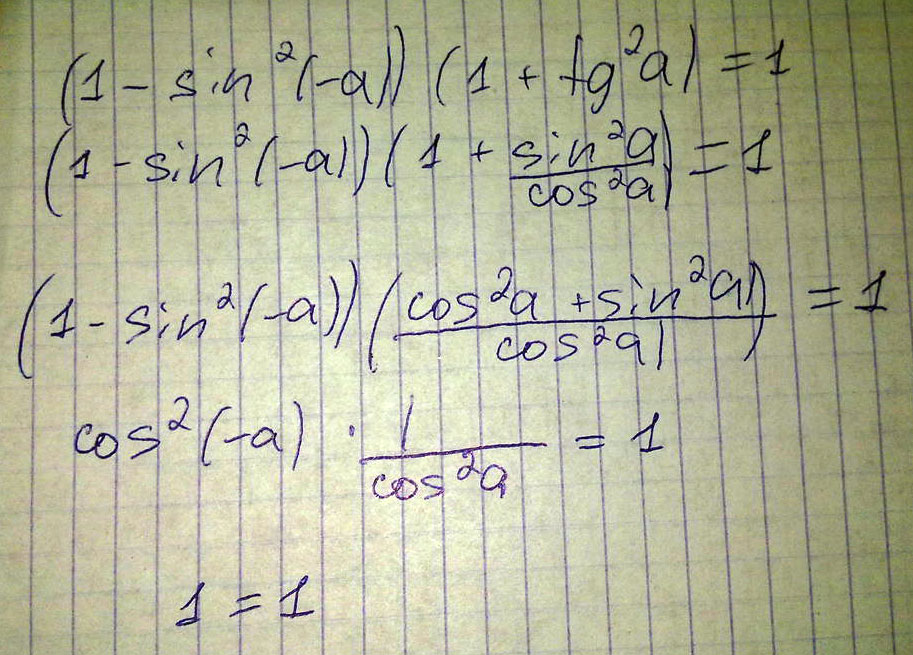тождество »
как доказать тождество - страница 24
Помогите доказать тождество \( tg( \frac{ \pi }{3}+ \alpha )- tg( \frac{ \pi }{3}- \alpha )=\frac{ 8tg \alpha }{1- 3tg ^{2} \alpha } \)
Решение: $$ tg( \frac{ \pi }{3}+ \alpha )= \frac{tg \frac{ \pi }{3}+tg \alpha }{1-tg \frac{ \pi }{3}tg \alpha }= \frac{ \sqrt{3}+tg \alpha }{1- \sqrt{3}tg \alpha } \\ tg( \frac{ \pi }{3}- \alpha )= \frac{tg \frac{ \pi }{3}-tg \alpha }{1+tg \frac{ \pi }{3}tg \alpha }=\frac{ \sqrt{3}-tg \alpha }{1+ \sqrt{3}tg \alpha } \\ tg( \frac{ \pi }{3}+ \alpha )- tg( \frac{ \pi }{3}- \alpha )= \frac{ \sqrt{3}+tg \alpha }{1- \sqrt{3}tg \alpha } - \frac{ \sqrt{3}-tg \alpha }{1+ \sqrt{3}tg \alpha } = \\ = \frac{( \sqrt{3}+tg \alpha)(1+ \sqrt{3}tg \alpha) }{(1- \sqrt{3}tg \alpha)(1+\sqrt{3}tg \alpha) }- \frac{( \sqrt{3}-tg \alpha)(1- \sqrt{3}tg \alpha) }{(1+ \sqrt{3}tg \alpha)(1- \sqrt{3}tg \alpha) }= $$
$$ =\ \frac{( \sqrt{3}+tg \alpha)(1+ \sqrt{3}tg \alpha)- ( \sqrt{3}-tg \alpha)(1- \sqrt{3}tg \alpha) }{(1- \sqrt{3}tg \alpha)(1+\sqrt{3}tg \alpha) } = \\ \ \frac{ \sqrt{3}+tg \alpha+3tg \alpha+ \sqrt{3}tg ^{2} \alpha - \sqrt{3}+tg \alpha+3tg \alpha - \sqrt{3}tg ^{2} \alpha }{(1- \sqrt{3}tg \alpha)(1+\sqrt{3}tg \alpha) }= \\ = \frac{ 8tg \alpha }{1- 3tg ^{2} \alpha } $$
Помогите доказать Тождество \((\frac{4a}{a^2 -1}+\frac{a-1}{a+1})\cdot \frac{2a}{a+1}-\frac{a}{a-1}-\frac{a}{a^2 -1}=\frac{a^2}{a^2 -1} \)
Решение: 1)(4a/(a²-1) + (a-1)/(a+1))*2a/(a+1) - a/(a-1) - a/(a²-1)=a²/(a²-1)
4a/(a-1)(a+1) +(a-1)/(a+1)=(4a+a²-2a+1)/(a-1)(a+1)=(a+1)²/(a-1)(a+1)=(a+1)/(a-1)
(a+1)/(a-1)*2a(a+1)=2a/(a-1)
2a/(a-1) -a/(a-1) -a/(a²-1)=a/(a-1) -a/(a-1)(a+1)=(a²+a-a)/(a-1)(a+1)=a²/(a²-1)
a²/(a²-1)=a²/(a²-1)
2)[2ab/(a²-b²) + (a-b)/2(a+b) ]* 2a/(a+b) - b/(a-b)=1
2ab/(a²-b²) + (a-b)/2(a+b) =(4ab+a²-2ab+b²)/2(a²-b²)=(a+b)²/2(a²-b²)=
=(a+b)²/2(a-b)(a+b)=(a+b)/2(a-b)
(a+b)/2(a-b)*2a/(a+b)=a/(a-b)
a/(a-b) - b/(a-b)=(a-b)/(a-b)=1
1=1

Доказать тождество: \((1-sin^2(-a))(1+td^2a)=1 \)
Решение: $$ (1+ sin^{2} \alpha )* \frac{1}{ cos^{2} \alpha } =1 \\ \frac{ cos^{2} \alpha }{ cos^{2} \alpha } =1 \\ 1=1 $$
Тождество доказано
Доказать тождество (tga+ctga)*sina*cosa=1
Решение: $$ (tga+ctga)*sina*cosa=1\\\\(\frac{sina}{cosa}+\frac{cosa}{sina})*sina*cosa=1\\\\\frac{sin^2a+cos^2a}{sina*cosa}*sina*cosa=1\\\\sin^2a+cos^2a=1\\\\1=1 $$$$ (tga+ctga)*sina*cosa \\ tga+ctga=sina/cosa+cosa/sina=(sin^2a+cos^2)/(sina*cosa) \\ (sin^2a+cos^2a)/(sina*cosa) *sina*cosa=sin^2a+cos^2a $$
По основному тригонометрическому тождеству:
$$ sin^2a+cos^2a=1 $$
Итак,$$ (tga+ctga)*sina*cosa=1 $$
Что и требовалось доказать
Помогите доказать тождество
(3+4cos(4A)+cos(8A))/(3-4cos(4A)+cos(8A))=ctg^(4)2A
Решение: Числитель 4cos 4a+(1+cos 8a)+2=4cos 4a+2(cos 4a)^2+2Знаменатель -4cos 4a+(1+cos 8a)+2=2(cos 4a)^2+2-4cos 4a
Для простоты обозначим cos 4a=t
4cos 4a+2(cos 4a)^2+2=2t^2+4t+2=2(t^2+2t+1)=2*(t+1)^2
2(cos 4a)^2+2-4cos 4a=2t^2-4t+2=2*(t^2-2t+1)=2(t-1)^2=2*(1-t)^2
Сокращаем на 2 и получаем ((t+1)^2)/((1-t)^2)=(1+cos 4a)^2/(1-cos 4a)^2=
(2*(cos 2a))^2)^2/(2*(cos 2a))^2)^2=(cos 2a)^4/(sin 2a)^4=(ctg 2a)^4
Здесь используется формула (1+cos 2a)=2*(cos a)^2,(1-cos 2a)=2*(sin a)^2