тождество »
как доказать тождество - страница 25
Нужно доказать тождество \( x^{2} - 12x +45 = (x-15)(x+3) \)
Решение: Нужно просто раскрыть скобки в правой части тогда получаетсях2+3х-15х+45=х2-12х+45, что равно левой части.
нужно раскрыть скобки в любой из частей, тогда получится правая часть = левой части.
Я хочу раскрыть правую часть (на выбор):
х2-12х+45= (перемножаем скобки): х2+3х-15х-45
х2-12х+45=х2-12х+45
Тождество доказано.
)
Помогите доказать тождество: (tg(9пи/4)+tg(5пи/2-а))^2+(ctg(5пи/4)+ctg(пи-а))^2 = 2/sin^2(a)
Решение: (tg(9пи/4)+tg(5пи/2-а))^2+(ctg(5пи/4)+ctg(пи-а))^2 = 2/sin^2(a)
Доказательство
Преобразуем левую часть выражения
tg(9пи/4)+tg(5пи/2-а) =tg(2пи+пи/4)+tg(2пи+пи/2-а)=
=tg(пи/4)+tg(пи/2-а) =1+ctg(a)
ctg(5пи/4)+ctg(пи-а) = ctg(пи+пи/4)-ctg(а) =ctg(пи/4)-ctg(a)=
=1- ctg(a)
(tg(9пи/4)+tg(5пи/2-а))^2+(ctg(5пи/4)+ctg(пи-а))^2 =
=(1+ctg(a))^2 + (1-ctg(a))^2 = 1 + 2ctg(a) + ctg^2(a) + 1 - 2ctg(a) + ctg^2(a) =
=2 + 2ctg^2(a) = 2(1+ cos^2(a)/sin^2(a))=
=2*(sin^2(a) + cos^2(a))/sin^2(a) = 2/sin^2(a)
Нужно доказать тождество. \( \frac{(cosa+sina)^2-1}{sin^2a-cos^2a-1}+tga=0 \)
Решение: $$ \frac{(cosa+sina)^2-1}{sin^2a-cos^2a-1}+tga=0 \\ \frac{cos^2a+2sina*cosa+sin^2a-1}{sin^2a-cos^2a-sin^2a-cos^2a}+tga=0 \\ \frac{2sina*cosa}{-2cos^2a}+tga=0 \\ -\frac{sina}{cosa}+tga=0 \\ -tga+tga=0 \\ 0=0 $$
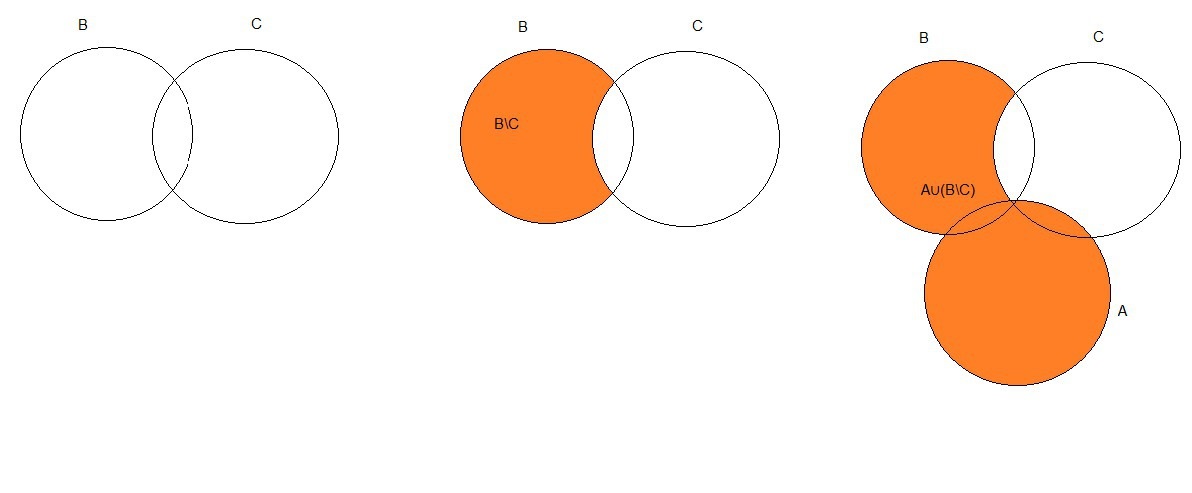
ДоказаноДоказать тождество \( A\cup (B/C)=(A\cup B)/(C/A) \)
Решение: Все во вложении, открывать картинки по порядку.
Доказательство сделано при помощи кругов Эйлера. В первых трех картинках, я поэтапно показал множество $$ A\cup (B/C) $$
В последних четырех я поэтапно показал множество $$ (A\cup B)/(C/A) $$. Так как результаты совпадают, значит и множества совпадают. Ч. Т. Д
Помогите доказать тождество \( \frac{sin \alpha +cos \alpha }{ \sqrt{2} }=cos( \alpha - \frac{ \pi }{4} ) \)
Решение: Приведем правую часть к левой по формуле:
$$ cos( \alpha - \beta )=cos \alpha *cos \beta +sin \alpha *sin \beta \\ cos( \alpha - \frac{ \pi }{4} )=cos \alpha *cos\frac{ \pi }{4}+sin \alpha *sin\frac{ \pi }{4}=cos \alpha * \frac{ \sqrt{2} }{2} +sin \alpha * \frac{ \sqrt{2} }{2} \\ \frac{ \sqrt{2} }{2} = \frac{ \sqrt{2}}{ \sqrt{2}* \sqrt{2}} = \frac{1}{ \sqrt{2}} $$
Поэтому:
$$ cos \alpha * \frac{ \sqrt{2} }{2} +sin \alpha * \frac{ \sqrt{2} }{2}=cos \alpha * \frac{1 }{ \sqrt{2} } +sin \alpha * \frac{1}{ \sqrt{2} }= \\ = \frac{cos \alpha }{ \sqrt{2} }+ \frac{sin \alpha }{ \sqrt{2} }= \\ = \frac{cos \alpha +sin \alpha }{ \sqrt{2} } =\frac{sin \alpha +cos \alpha }{ \sqrt{2} } $$-ч. т. д.

