тождество »

как доказать тождество - страница 22

  • Доказать тождество (2а/а+3-4а/а^2+6а+9) а+1/а^2-9-а^2-9а/а+3=а


    Решение: Доказать тождество
    [2а/(а+3)-4а/(а^2+6а+9)] :[(а+1)/(а^2-9)] - (а^2-9а)/(а+3)=а
    [2а/(а+3)-4а/(а^2+6а+9)] :[(а+1)/(а^2-9)] - (а^2-9а)/(а+3)
    1) [2а/(а+3)-4а/(а^2+6а+9)]=[(2а(а+3)-4а)/((а+3)^2)]=2a(a+1)/((а+3)^2
    2) (а+1)/(а^2-9)=(а+1)/[(а-3)(a+3)]
    3) [2a(a+1)/((а+3)^2] :[(а+1)/(а^2-9)]=
    =[2a(a+1)/((а+3)^2] · [(а-3)(a+3)]/(а+1)=2a(a-3)/(a+3)
    4)2a(a-3)/(a+3)- (а^2-9а)/(а+3)=[2a^2-6a-a^2+9a]/(a+3)=(a^2+3a)/(a+3)=a(a+3)/(a+3)=a

  • Доказать тождество
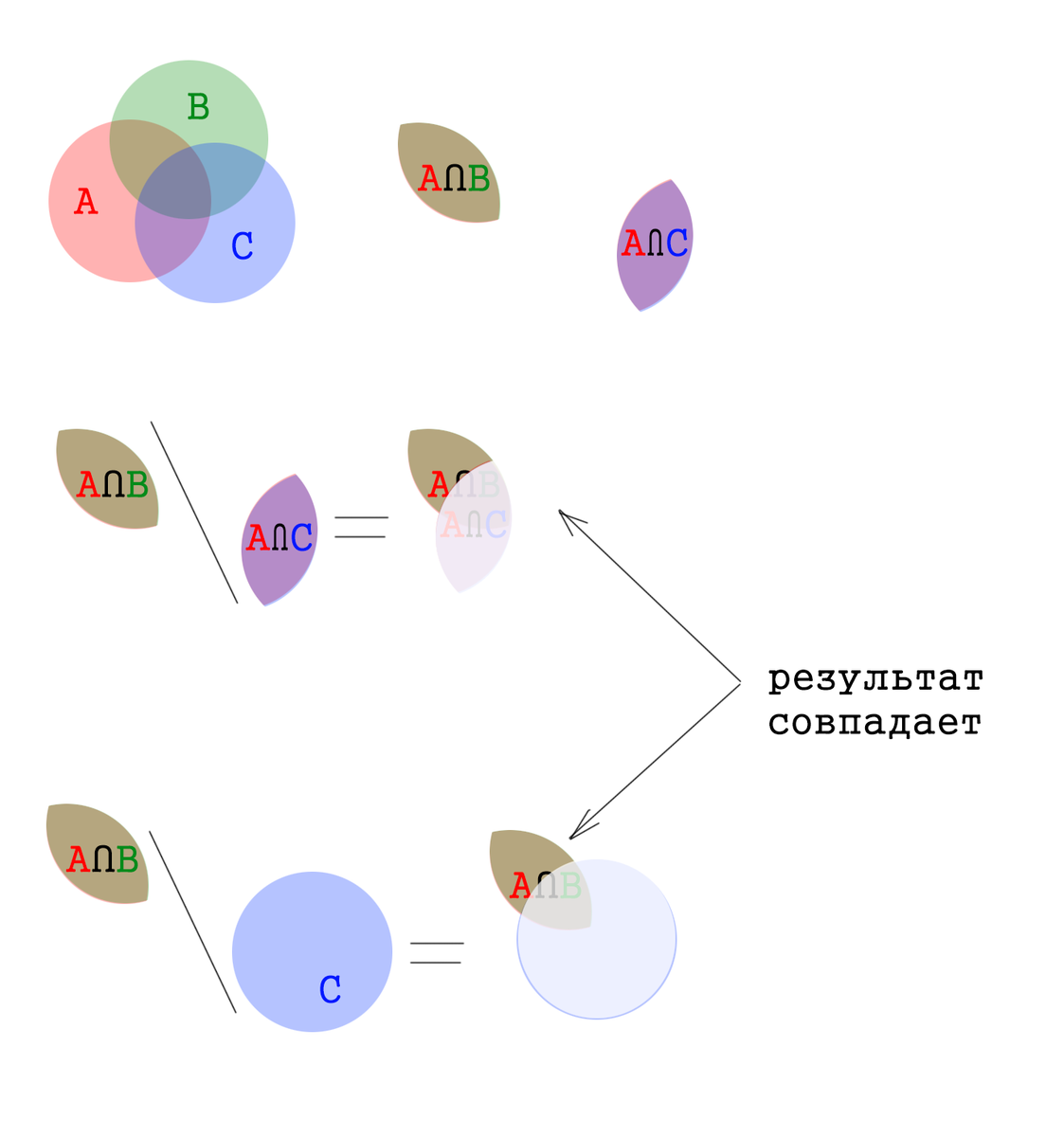
    (A∩B)\(A∩C)=(A∩B)\C


    Решение:
    Всегда верно, что X\Y = X∩{–Y}, где {–Y} – обратное к Y множество.
    Всегда верно, что { –(Y∩Z) } = (–Y) U ( –Z ) ;
    Всегда верно, что X∩(YUZ) = [ X∩Y ] U [ X∩Z ] ;
    Всегда верно, что X∩(–X) = { 0 }, где { 0 } – ноль-множество.
    (A∩B)\(A∩C) = ( A∩B ) ∩ { –(A∩C) } = ( A∩B ) ∩ { (–A) U (–C) } =
    = [ (A∩B)∩(–A) ] U [ (A∩B)∩(–C) ] = { 0 } U [ (A∩B)∩(–C) ] = (A∩B)\C
    Что и требуется доказать.

    Всегда верно что X Y X Y где Y обратное к Y множество.Всегда верно что Y Z Y U Z Всегда верно что X YUZ X Y U X Z Всегда верно что X X где ноль-множество. A B A C A B A C A B...

  • доказать тождество (sin5a + sin3a)/2sin4a = cosa


    Решение: (sin5a + sin3a)/2sin4a = cosa

    а иначе можно подумать, что тут дробь sin3a/2sin4a плюс sin5a, а в таком случае тождество не докажете.

    Решение.

    В числителе воспользуемся формулой суммы синусов с разными аргументами (sinx + siny = 2sin((x+y)/2))*cos((x-y)/2), получим:

    2sin4a*cosa/2sin4a = cosa

    2sin4a сократим и получим:

    cosa = cosa

    Ч. Т. Д.

  • Доказать тождество: 1)(b+3)(b+6)=b^2 +18; 2)(b+1)(b+2)(b+3)=b^3 +2b^2 +3b; 3) y^3 =(y+1)(y^2 -1); 4)y^2 +y+1=(y+1)^2


    Решение: 1) (b+3)*(b+6) = b^2+18

    9 = 0

    b = 0

    0

    Ответ: b = 0.

    2) (b+1)*(b+2)*(b+3) = b^3+2*b^2+3*b

     b ∈ ∅; 

     b ∈ ∅; b = -(sqrt(2)*%i+2)/2;b = (sqrt(2)*%i-2)/2;

    Ответ: нет действительных решений.

    3) y^3 = (y+1)*(y^2-1)

    y=1/2-корень(5)/2, y=корень(5)/2+1/2

    Ответ: y=корень(5)/2+1/2.

    4) y^2+y+1 = (y+1)^2

    -y = 0

    0

    y = 0

    Ответ: y = 0.

  • Доказать тождество.
    \( (cos\alpha -cos\beta )^2 +(sin\alpha -sin\beta )^2=\\=4sin^2 (\alpha - \beta /2) \)
    решить.


    Решение: $$ \alpha =x\\ \beta =y\\(cosx-cosy)^2+(sinx-siny)^2=4sin^2 \frac{x-y}{2}\\cos^2x-2cosx cosy+cos^2y+sin^2x-2sinx siny+sin^2y=\\=-2(cosx cosy+sinx siny)=-2cos(x-y)=-2(cos^2 \frac{x-y}{2}-sin^2 \frac{x-y}{2})=\\=4sin^2 \frac{x-y}{2}-2 $$

    $$ (cosa-cosy)^2+(sina-siny)^2=\\ =cos^2a-2*cosa*cosy+cos^2y+sin^2a-2*sina*siny+sin^2y=\\ =1-2*cosa*cosy+1-2*sina*siny=\\ =2-2(cosa*cosy-sina*siny)=\\ =2-2*cos(y-a) $$
    Тут где-то напутано, ибо
    $$ 4sin^2(a-y/2)=2-2cos(y-2a) $$

<< < 202122 23 24 > >>