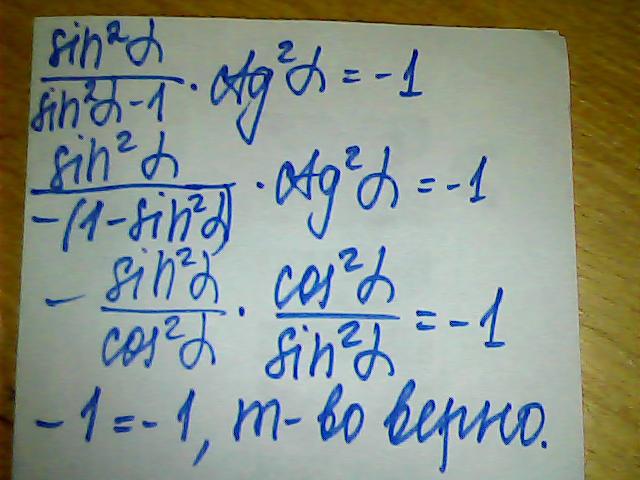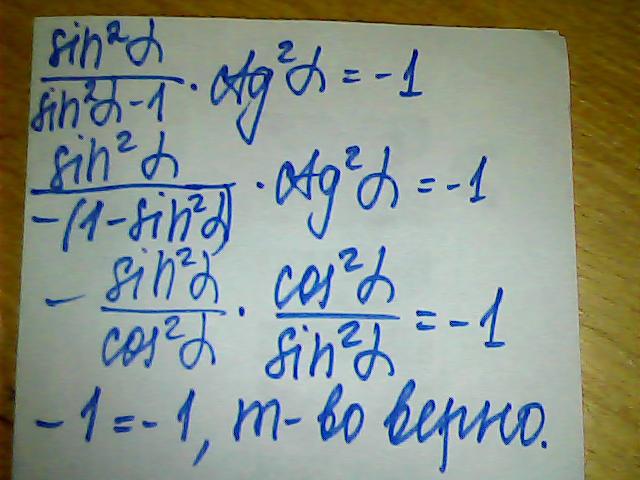тождество »
как доказать тождество - страница 21
Доказать тождество \( 1 + sin \alpha = \frac{cos \alpha + ctg \alpha }{ctg \alpha } \)
Решение: Преобразуем правую часть доказываемого тождества. Для этого почленно разделим числитель на знаменатель:
$$ \frac{cos \alpha + ctg \alpha }{ctg \alpha } = \frac{ctg \alpha }{ctg \alpha } + \frac{cos \alpha }{ctg \alpha } = 1 + sin \alpha $$
Последнее выражение получено, исходя из того, что
$$ \frac{cos \alpha }{ctg \alpha } = cos \alpha : \frac{cos \alpha }{sin \alpha }= \frac{cos \alpha sin \alpha }{cos \alpha } = sin \alpha $$
Путём преобразования правой части, мы получили левую(причём, равенство верно для всех \(\alpha\) из области определения выражения). Поэтому тождество верно.
Доказать тождество. Решить подробно. \( (cos^{-1}2\alpha + ctg(\frac{5}{2}\pi + 2\alpha)) ctg(\frac{5}{4}\pi - \alpha) = tg\frac{\pi}{4}\)
Решение: (cos^(-1) 2α-ctg(5/2 π+2α))·ctg(5/4π+2α)=tg(π/4)
Упростим каждое выражение:
cos^(-1) 2α=1/cos2α/
ctg(5/2π+2α)=ctg(π/2 +2α)=tg2α=sin2α/cos2α.
ctg(5/4π-α)=ctg(π/4-α)=(1+tg45°·tgα)/(tg45°-tgα)=(1+tgα)=(1-tgα); tg45°=1.
tg(π/4)=tg45°=1/
Данное в условии равенство примет вид:
(1/cos2α-(sin2α/cos2α))·((1+tgα)/(1-tgα))=1;
((1-sin2α)/cos2α)·(1+sinα/cosα)/(1-sinα/cosα)=1;
((1-sin2α)/cos2α)·(cosα+sinα)/(cosα-sinα)=1; здесь было сокращение на cosα);
(1-sin2α)/((cosα-sinα)(cosα+sinα))·((sinα+cosα)/(cosα-sinα))=1;
произведем сокращение на выражение (sinα+cosα);
((1-sin2α)/(cosα-sinα))·((1/(cosα-sinα))=1;
(1-sin2α)/(cosα-sinα)²=1;
Дробь равна 1, если числитель равен знаменателю
(1-sin2α)=(cosα-sinα)²;
1-2sinα·cosα=cos²α-2sinα·cosα+sin²α;
1=cos²α+sin²α;
1=1.
ч. т. д.
Доказать тождество
(sina)^2 + (sinb)^2 + (sinc)^2 - 2cosa cosb cosc = 2, a+b+c=180^0
Решение: $$ sin^2a+sin^2b+sin^2c-2cosa\cdot cosb\cdot cosc=2\;,\; \; a+b+c=180^\circ \\\\sin^2a+sin^2b+sin^2c=2+2cosa\cdot cosb\cdot cosc\\\\sin^2a+sin^2b+sin^2c= \frac{1-cos2a}{2} + \frac{1-cos2b}{2} + \frac{1-cos2c}{2} =\\\\= \frac{3}{2} -\frac{1}{2} (cos2a+cos2b+cos2c)=\frac{1}{2}(3-(cos2a+cos2b)-cos2c)=\\\\=\frac{1}{2}(3-2cos(a+b)\cdot cos(a-b)- (2cos^2c-1))=\\\\=\frac{1}{2}(4-2cos(180^\circ -c)\cdot cos(a-b)-2cos^2c)=\\\\=\frac{1}{2}(4+2cosc\cdot cos(a-b)-2cos^2c)=2+cosc\cdot cos(a-b)-cos^2c= \\ =2+cosc\cdot (cos(a-b)-cosc)=[\; c=180^\circ -(a+b)\ ]=\\\\=2+cosc\cdot(cos(a-b)-cos(180^\circ -(a+b)))=\\\\=[\; cos(180^\circ - \alpha )=-cos \alpha \; ]=\\\\=2+cosc\cdot (cos(a-b)+cos(a+b))=\\\\=2+cosc\cdot 2cos \frac{a-b+a+b}{2} \cdot cos \frac{a-b-(a+b)}{2} =\\\\=2+cosc\cdot 2cosa\cdot cos(-b)=\\\\=2+2cosa\cdot cosb\cdot cosc\qquad \Rightarrow \\\\sin^2a+sin^2b+sin^2c-2cosa\cdot cosb\cdot cosc=2 $$
Доказать тождество: 25-х\4 - х+1\6=13-2х\3 + х+7\4
Решение: Нужно избавиться от знаменателя каждой дроби. Для этого умножаем каждую дробь на число которое содержит в себе числа всех знаменателей. У нас есть 6,4 и 3. Подходит число 12. Получиться:
12(25-х\4)-12(х+1\6)=12(13-2x\3)+12(x+7\4).
Далее сокращаем числа из знаменателей с 12.
3(25-х)-2(х+1)=4(13-2х)+3(х+7). Далее обычная арифметика.
Ответ: 73-5x=73-5xДоказать тождество:\( \frac{sin^2\alpha}{sin^2\alpha -1}\cdot ctg^2\alpha = -1 \)
Решение: В знаменателе появился косинус по средствам использования формулы тригонометрической единицы и выражение из неё косинуса.