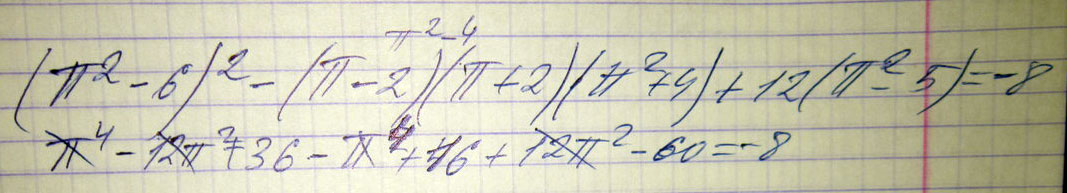как доказать тождество - страница 19
Доказать тождество
2sina+sin2a / 2sina-sin2a = ctg^2 a/2
Решение: $$ \frac{2sin a+sin(2a)}{2sin a-sin(2a)}= $$
используем формулу синуса двойного угла
$$ \frac{2sin a+2 sin a cos a}{2sin a-2sin a cos a}= $$
сокращаем на 2sin a
$$ \frac{1+cos a}{1-cos a}= $$
используем формулы понижения степени
$$ \frac{2cos^2 \frac{x}{2}}{2sin^2 \frac{x}{2}}= $$
сокращаем и одно из основных соотношений
$$ ctg^2 \frac{x}{2} $$
доказать тождество sin3a+sin3a/sina +cos3a -cos3a/cosa = 3
Решение: sin3a + sin3a/sina + cos3a - cos3a/cosa = 3
1) sin3a = 3sina - 4sin³a
2) cos3a = 4cos³a - 3cosa
sin3a + cos3a + sina*(3 - 4sin²a)/sina - cosa*(4cos²a - 3)/cosa = 3
sin3a + cos3a + 3 - 4sin²a - 4cos²a + 3 = 3
sin3a + cos3a - 4(sin²a + cos²a) + 6 = 3
sin3a + cos3a - 4 + 6 = 3
sin3a + cos3a + 2 = 3
(sin3a + cos3a -> должно ровняться 1, но как разложить дальше, я не знаю.)
Ûßö.=)
Доказать тождество:
cos(\( \alpha + \beta \)) + sin(-\( \alpha \)) * sin(-\( \beta \)) = cos\( \alpha \) cos\( \beta \)
Решение: Cos( \alpha + \beta ) + sin(- \alpha ) * sin(- \beta ) = cos \alpha * cos \beta - sin \alpha * sin \beta + sin \alpha * sin \beta = cos \alpha * cos \betaДоказать тождество:
(п² - 6)² - (п-2)×(п+2)×(п²+4) + 12×(п²-5) = -8
Решение: .(P.S раскрывай скобки, возводи в квадраты, применяй формулы, учитывай знаки, и всё получается.)
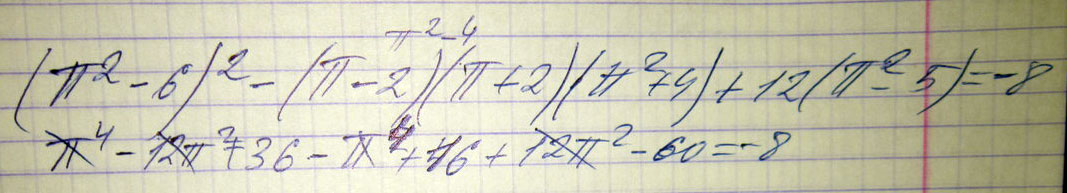
Доказать тождество: 1.1 \(\frac{cos\alpha}{tg^2\frac{\alpha}{2}-ctg^2\frac{\alpha}{2}}= -\frac{1}{4}sin^2\alpha \)
1.3 \( \frac{1+2sin\alpha cos\alpha}{sin^2\alpha-cos^2\alpha}=\frac{tg\alpha +1}{tg\alpha -1} \)
Решение: 1.1))) здесь все важные преобразования в знаменателе.отдельно знаменатель = (sin(a/2))^2 / (cos(a/2))^2 = (cos(a/2))^2 / (sin(a/2))^2 =
((sin(a/2))^4 - (cos(a/2))^4) / ((sin(a/2))^2*(cos(a/2))^2) =
((sin(a/2))^2 - (cos(a/2))^2)*((sin(a/2))^2 + (cos(a/2))^2) / ((sin(a/2))^2*(cos(a/2))^2) =
((sin(a/2))^2 - (cos(a/2))^2)*1/ ((sin(a/2))^2*(cos(a/2))^2) =
-4cos(a) / (sin(a))^2
все выражение = cos(a) * (sin(a))^2 / (-4cos(a)) = -(sin(a))^2 / 4
1.3))) числитель можно записать так: (sina)^2 + (cosa)^2 + 2sina*cosa = (sina + cosa)^2
знаменатель: (sina - cosa)(sina + cosa)
получим: (sina + cosa) / (sina - cosa)
c другой стороны (tga + 1) / (tga - 1) = (sina/cosa + 1) / (sina/cosa - 1) =
(sina + cosa) / cosa разделить на дробь (sina 1-cosa) / cosa =
(sina + cosa) / cosa умножить на дробь cosa / (sina 1-cosa) = (sina + cosa) / (sina - cosa)