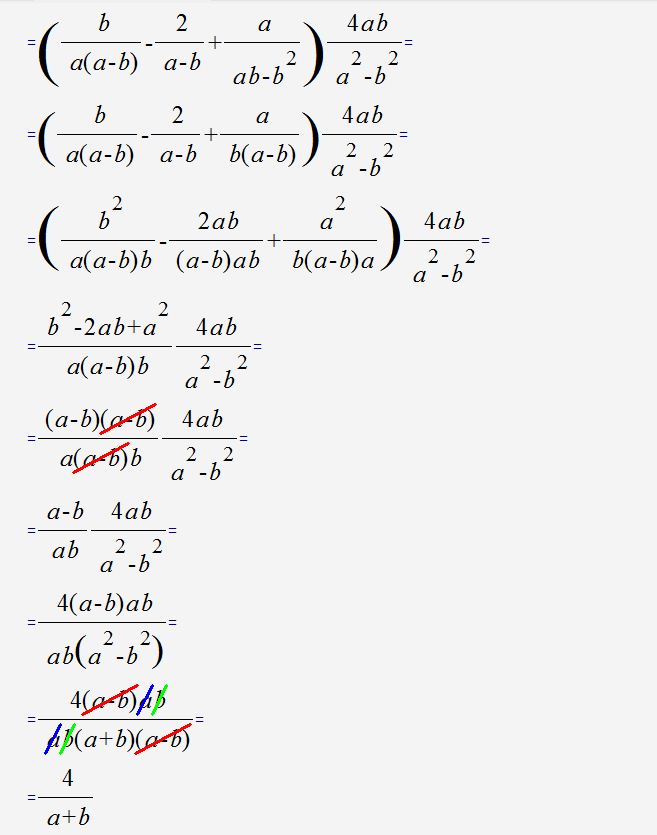как доказать тождество - страница 17

доказать тождество (довести тотожність).

доказать тождество (довести тотожність) \( (\frac{b}{a^2 -ab} - \frac{2}{a-b} - \frac{a}{b^2 -ab}): \frac{a^2 - b^2}{4ab}= \frac{4}{a+b} \)

Если левая часть тождества равна правой, значит оно верно или тождественно равно))

Левая часть = $$ (\frac{b}{a^{2}-ab}-\frac{2}{a-b}-\frac{a}{b^{2}-ab}):\frac{a^{2}-b^{2}}{4ab}=\\=(\frac{b}{a(a-b)}-\frac{2}{a-b}-\frac{a}{b(b-a)}):\frac{(a-b)(a+b)}{4ab} $$

приведём скобку к общему знаменателю:

=$$ (\frac{b^{2}-2ab+a^{2}}{ab(a-b)}):\frac{a^{2}-b^{2}}{4ab} $$

В числителе видим формулу квадрат разности:

=$$ \frac{(b-a)^{2}4ab}{ab(a-b)(a-b)(a+b)}=\frac{4}{a+b} $$ Что и требовалось доказать.

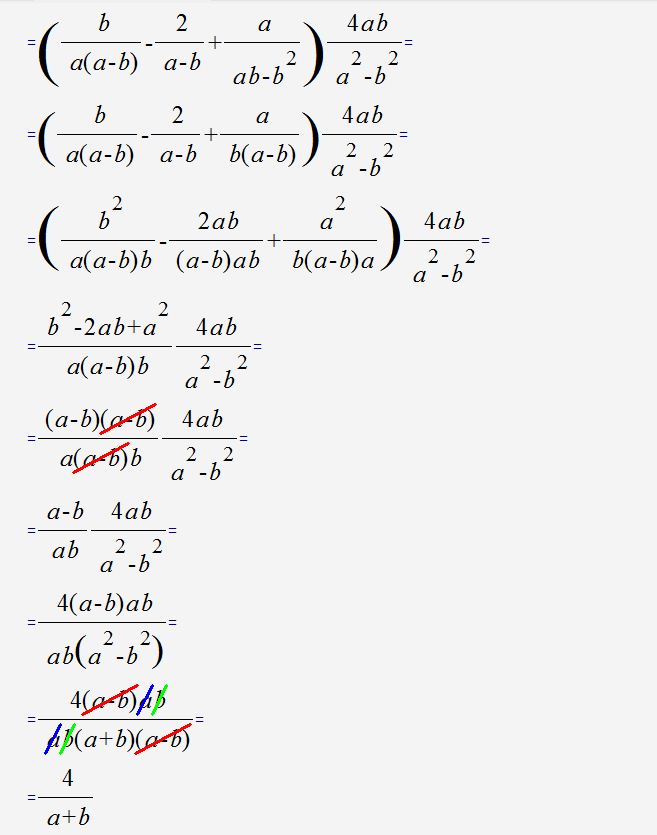
Доказать тождество
(((2a/(a+3)) - ((4a/(a^2+6a+9)))/((a+1)/(a^2-9)) - ((a^2-9a)/(a+3)) = a

Доказать тождество. \( \frac{x^2 - 8y^2}{x^{\frac{2}{3}}-2\sqrt{y^2}}-(x^{\frac{2}{3}}+2\sqrt{y^2})^2 \)

Доказать тождество с двумя способами
A∧(B∧C)=(A∧B)∨C

(A∧B)∨C=(C∨A)∧(C∨B)-по закону распределения ⇒A∧B∧C=(C∨A)∧(C∨B)

Решение во вложенном файле)