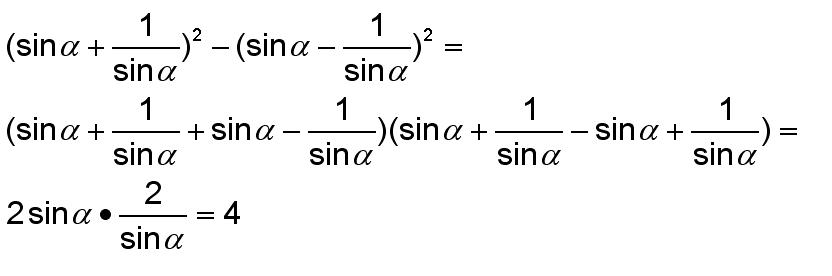как доказать тождество - страница 15
На какое выражение нужно заменить *, чтобы равенство 27-с^6=(3-с^2)(*) стало тождеством?
Решение: $$ 27-c^6=3^3-(c^2)^3=(3-c^2)(3^2+3c^2+(c^2)^2)= \\ =(3-c^2)(9+3c^2+c^4) $$Решить: 1) доказать тождество 1=sin^(2)a+ctg^(2)asin^(2)a
2) найти площадь фигуры ограниченную линиями:
Y=x^2; y=-3x
Решение: $$ sin^{2} \alpha + ctg^{2} \alpha *sin^{2} \alpha =1 \\ sin^{2} \alpha + \frac{cos ^{2} \alpha *sin ^{2} \alpha }{sin ^{2} \alpha } =1 $$
Синус квадрат альфа сократиться, и получится основное тригонометрическое тождество:
$$ sin^{2} \alpha + cos^{2} \alpha =1 $$
1)sin²a+cos²a/sin²a *sin²a=sin²a+cos²a=1
1=1
2)x²=-3x⇒x²+3x=0⇒x(x+3)=0⇒x=0 U x=-3
s=S(от -3 до 0)(-3x-x²)dx=-3x²/2-x³/3(от -3 до 0)=27/2-9=4,5кв ед
Доказать тождество:
\((sin\alpha+ 1/sin\alpha)^2 - (sin\alpha - 1/sin\alpha)^2=4\)
Решение: . Решение основано на разложении разности квадратов чисел на произведение их суммы на разность.a^2-b^2=(a+b)(a-b)
Ограничением является условие sin(alfa) не равен 0, т. е alfa не равен 0
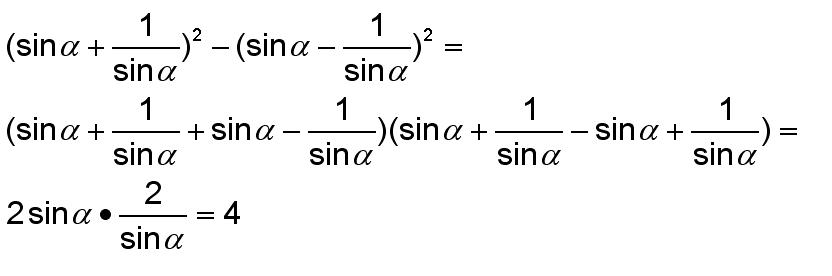
Помогите доказать тождество
(1+ctg2a)/(1-ctg2a) = sin(2a+п/4)/sin(2a-п/4)
Решение: Числитель 1 дроби 1 + Ctg 2a = 1 + Co2a/Sin2a = (Sin 2a +Cos 2a)/Sin 2a
знаменатель 1 дроби 1 - Ctg 2a = 1 - Cos 2a/Sin 2a = (Sin 2a - Cos 2a)/Sin 2a
После сокращения останется: (Sin 2a +Cos 2a)/ (Sin 2a - Cos 2a)
Числитель 2 дроби = Sin 2a Cos π/4 + Cos 2a Sinπ/4 = √2/2( Sin 2a + Cos 2a)
Знаменатель 2 дроби = Sin 2a Cos π/4 -Cos 2a Sinπ/4 =√2/2( Sin 2a - Cos 2a)
После сокращения останется :(Sin 2a +Cos 2a)/ (Sin 2a - Cos 2a)
Правая и левая части равны ⇒ тождество доказано.доказать тождество
ctg a - ctg 2a = 1/sin 2a
Решение: ctg (a) - ctg (2a)=использовав формулу для котангенса двойного угла, получим
=ctg (a) - (ctg^ 2 (a) -1)/(2 *ctg (a))=
сведя к общему знаметелю=
=(ctg^2 (a) - (ctg^ 2 (a) -1)) / (2* ctg (a))=
раскрывая скобки
=(2*ctg^2 (a) - ctg^ 2 (a) +1)) /(2 * ctg (a))=
упрощая подобные
раскрывая скобки
=(ctg^ 2 (a) +1)) /(2 * ctg (a))=
=домножая на sin^2 (a) числитель и знаменатель, и использовав одно из основных тригонометрчиеских соотношений, получим
=(cos^ 2 (a) +sin^2 (a))) /(2 *cos (a)*sin a)=
использовав основное тригонометрическое тождество и формулу синуса двойного угла, получим=
= 1/(sin 2a),
а значит данное равенство является тождеством (левую часть путем преобрзования выражений привели в вид выражения в правой части).
Доказано