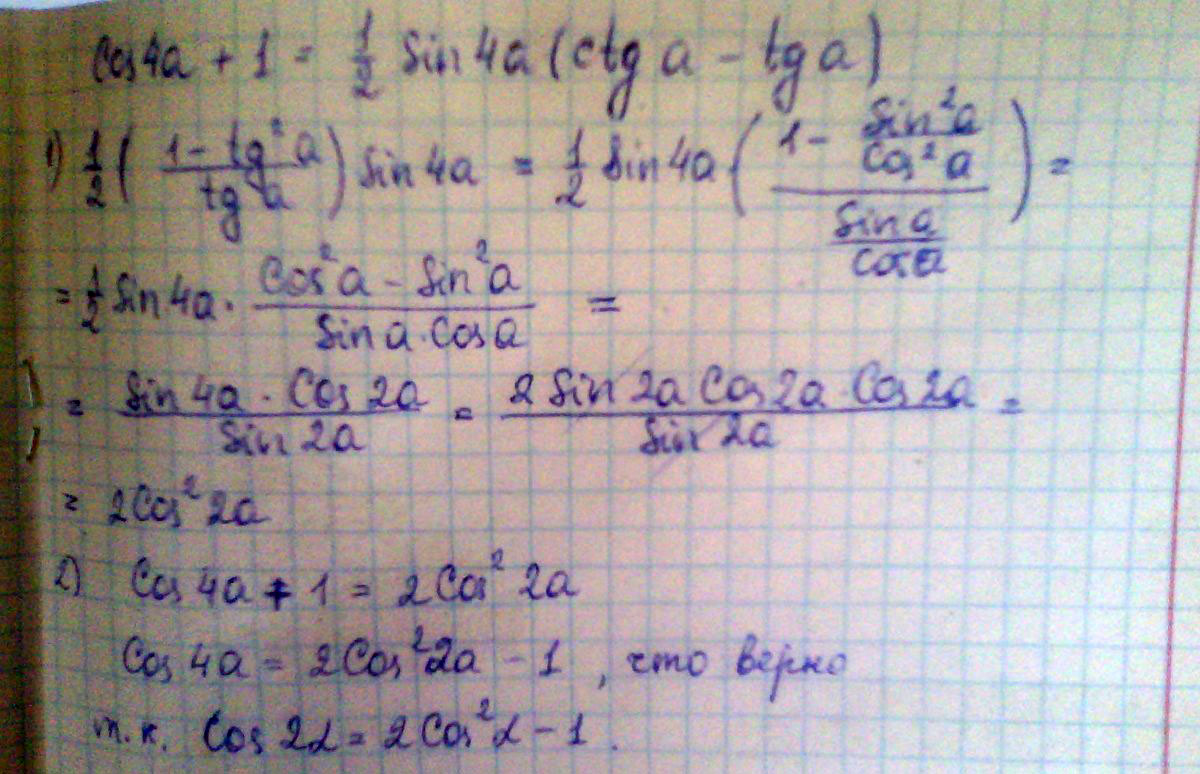как доказать тождество - страница 8
1. 1 - 4 sin^2 a cos^2 a/2 cos^2 a - 1. Упростить
2. \(\frac{tg(2a)* tg(a)}{tg(2a) - tg(a) }= sin(2a)\) Доказать тождество
Решение: 1 - 4 sin^2 a cos^2 a/2 cos^2 a - 1=1-sin^2(2a)/cos2a=cos^2(2a)/cos2a=cos2a(sin2a*sina)/(sin2a*cosa-sinacos2a)=sin2a*sina/sina=sin2a
вот решение второго:

Доказать тождество:
\( \frac{ctg \alpha }{ctg \alpha +tg \alpha } = cos^{2} \alpha \)
Решение: $$ ctg\alpha: \frac{1}{sin\alpha*cos\alpha} = \frac{cos\alpha}{sin\alpha} :\frac{1}{sin\alpha*cos\alpha} =cos^2\alpha \\ ctg \alpha +tg \alpha = \frac{cos\alpha}{sin\alpha} + \frac{sin\alpha}{cos\alpha} = \frac{cos^2\alpha+sin^2\alpha}{sin\alpha*cos\alpha} = \frac{1}{sin\alpha*cos\alpha} $$
$$ \frac{ctg \alpha }{ctg \alpha +tg \alpha } = \frac{ \frac{1}{tg \alpha } }{\frac{1}{tg \alpha }+tg \alpha } =\frac{1}{tg \alpha (\frac{1}{tg \alpha }+tg \alpha)}=\frac{1}{1+tg^2 \alpha }=\frac{1}{\frac{1}{cos^2 \alpha}}=cos^2 \alpha. $$
Доказать тождество: cos4a + 1 = 1/2 sin4a * (ctga - tga)
Решение: Используемые тождества$$ Sin2x= 2SinxCosx \\ Cos2x = Cos^2x - Sin^2x = 2Cos^2x - 1 $$
. Доказываем правую часть
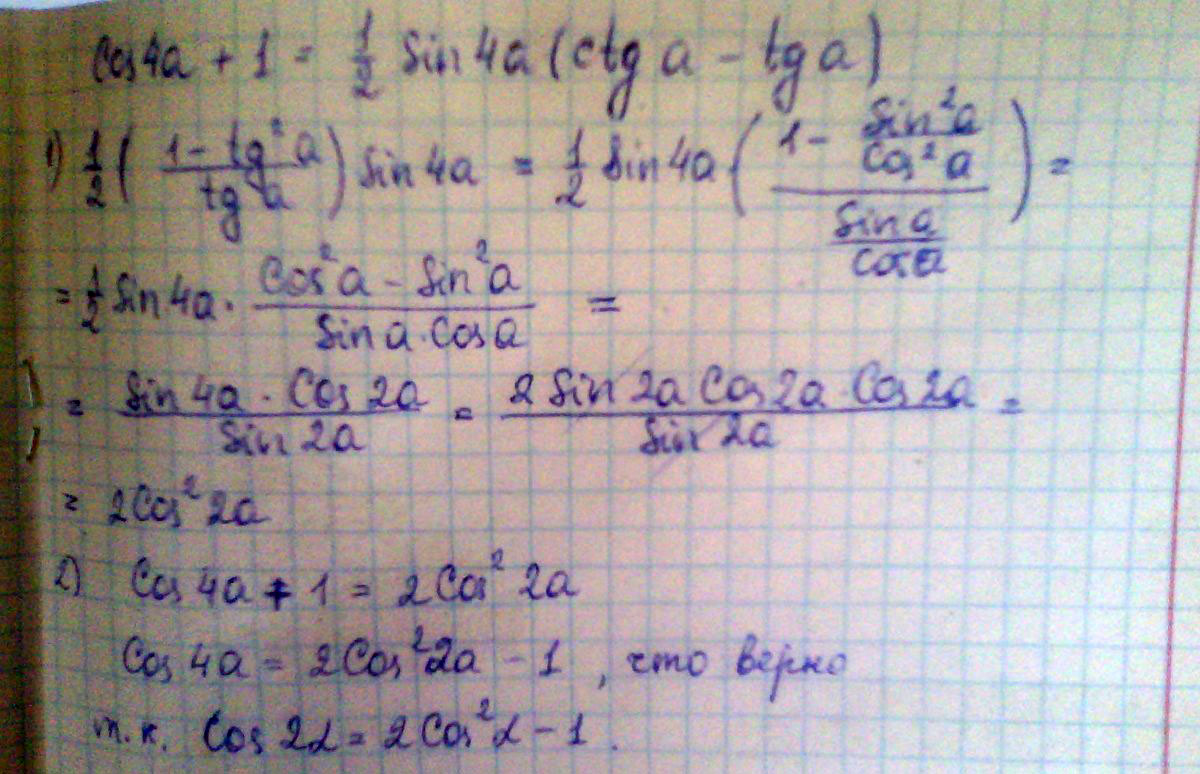
Помогите доказать тождество: sin(A+B) / sin(A-B) = tgA+tgB / tgA-tgB
Решение: Тождество доказываем, используя формулы синус суммы и разности:sin(A+B) sinA * cosB+sinB * cosA
- = - Разделим числитель и знаменатель на одно и то же
sin(A-B) sinA * cosB-sinB * cosA
выражение (cosA * cosB), не равное 0. Каждое слагаемое в числителе и в знаменателе разделится на это произведение. После сокращения получим
sinA/cosA +sinB/cosB tgA + tgB
- = - что и требовалось доказать. Левая часть=правой части
sinA/cosA-sinB/cosB tgA-tgB
Доказать тождество:
cos 4α + 1 = 0,5 sin 4α (ctg α – tg α)
Решение: Используя формулу для разности квадратов двух чисел, получаем:
sin 4a-cos 4a=(sin 2a+cos 2a) (sin 2a-cos 2a)
Но sin 2a+con 2a=1 Поэтому
sin 4a-con 4a= sin 2a-con 2a, что и требовалось доказать.