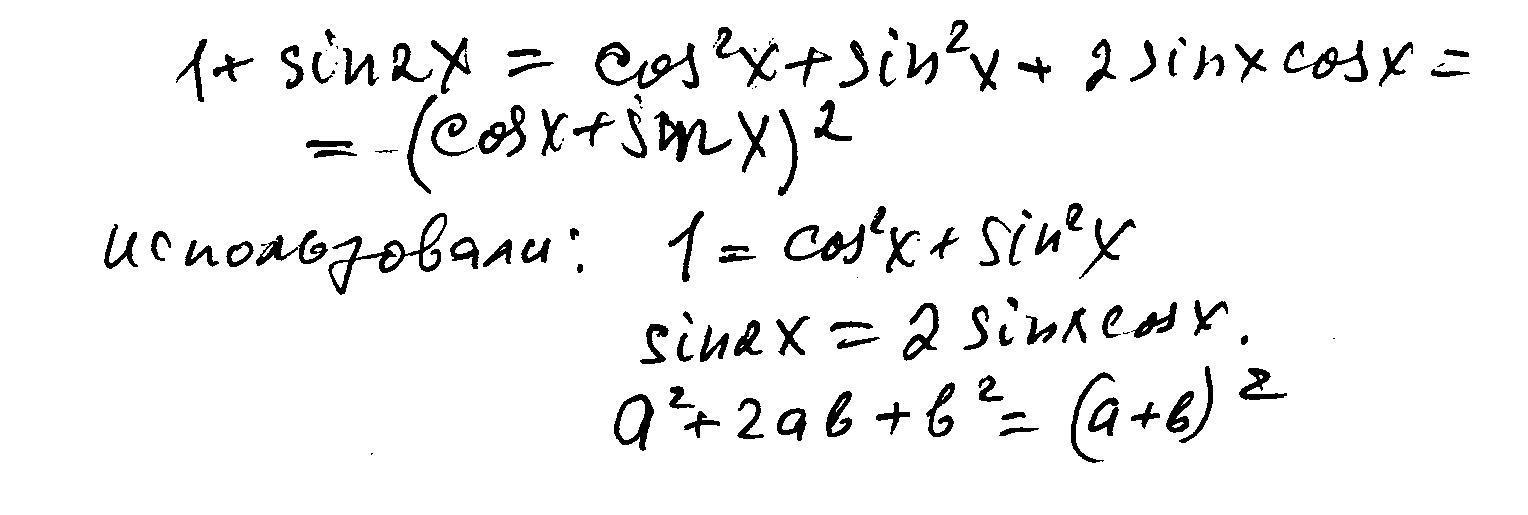тождество »
как доказать тождество - страница 10
Доказать тождество:
а) \( cos^{2} \alpha - sin^{2} \alpha( \pi/4 + \alpha )=\\= \frac{ \sqrt{2} }{2}sin( \pi /4 - 2 \alpha ) \)
б) \( (cos \alpha - cos \beta)^{2} - (sin \alpha - sin \beta) ^{2}=\\= -4sin ^{2} \frac{ \alpha - \beta }{2}cos( \alpha + \beta) \)
Вычислить:
\( tg( \frac{ \pi }{2} + arcctg 1). \)
\( cos(2arcctg1 - arcsin1 + arctg0) \)
Решение: $$ cos^2a-sin^2(\pi/4+a)=\frac{\sqrt{2}}{2}sin(\pi/4-2a)\\ \\ (cosa-sin(\pi/4+a))(cosa+sin(\pi/4+a))=\\=(\frac{-\sqrt{2}sina-\sqrt{2}cosa+2cosa}{2})(\frac{\sqrt{2}sina+\sqrt{2}cosa+2cosa}{2}) \\ \frac{2cos2a-2sin2a}{4}\\ \frac{\sqrt{2}}{2}*(\sqrt{2}/2cos2a-\sqrt{2}/2sin2a)=\\=\frac{2cos2a-2sin2a}{4}\\ $$
то есть обе части равны!
$$ (cosa-cosb)^2-(sina-sinb)^2=\\cos^2a-2cosa*cosb+cos^2b-sin^2a+2sina*sinb-sin^2b=\\= cos2a+cos2b-2cosa*cosb+2sina*sinb=cos2a+cos2b-2cos(a+b)\\ \\ -4sin^2\frac{a-b}{2}*cos(a+b)=\\=(2sina*sinb+2cosa*cosb-2)(cosa*cosb-sina*sinb) = \\=-2cos(a+b)+cos2b+sin2a $$
то есть тоже равны, сперва доказал справедливость левой, затем правой
$$ tg(90+arctg1)=\frac{-cos(arcctg1)}{sin(arcctg1)}=-ctg(arcctg1)\\ -ctg(arctg1)=-1 $$
Ответ -1
$$ cos(2arcctg1-arcsin1+arctg0)=cos(2arcctg1-arcsin1)=\\ cos(\frac{\pi}{2}-\frac{\pi}{2})=cos0=1 $$
Ответ 1Доказать тождество
1. 2 cos40° - cos20° / sin20° = √3
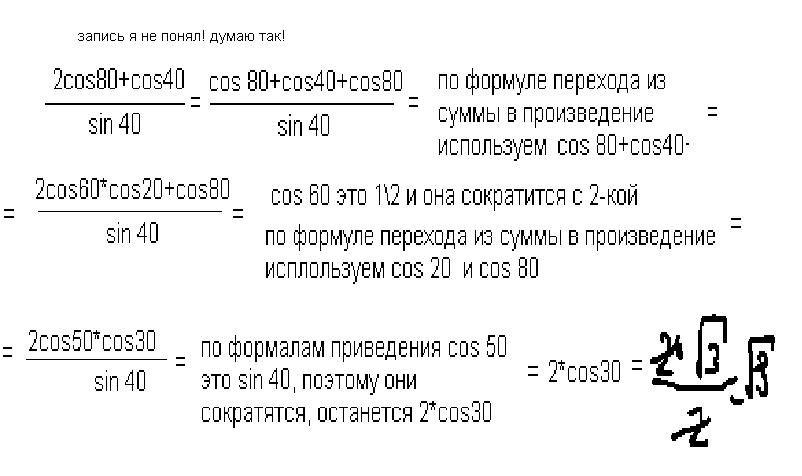
2. 2 cos80° + cos40° / sin40° = √3
Вычислить
6 sin 15° cos15° / 2 cos^2 15° - 1
Упросить
cos^2 (п-x) + cos^2 (3п/2 - x)
Решение: 6sin15cos15/2cos^215 -1= 3sin30/cos30=3tg30= √3cos^2(pi-x) +cos^2(3pi\2-x)= -cos^2x-sin^2x=-1(cos^2x+sin^2x)=-1
(2 cos80° + cos40°) / sin40° = √3 (синус общий знаменатель)
Аналогично доказываете первое тождество
Доказать тождество:
\( \frac{1-cos 4 \alpha }{cos \alpha -cos3 \alpha } \)=2 cos\( \alpha \)
Решение: $$ \frac{1-cos 4 \alpha }{cos \alpha -cos3 \alpha }=2 cos \alpha;\\ \frac{1-cos 4 \alpha }{cos \alpha -cos3 \alpha }=\frac{1-(1-2\sin^22\alpha)}{\cos\alpha-\cos(\alpha+2\alpha)}=\\ =\frac{1-1+2\sin^22\alpha}{\cos\alpha-\cos\alpha\cos2\alpha+\sin\alpha\sin2\alpha}=\\ =\frac{2\sin^22\alpha}{\cos\alpha-\cos\alpha(1-2\sin^2\alpha)+\sin\alpha\sin2\alpha}=\\ =\frac{2\sin^22\alpha}{\cos\alpha-\cos\alpha+2\sin^2\alpha\cos\alpha+\sin\alpha\sin2\alpha}=\\ \\ =\frac{2\sin^22\alpha}{2\sin^2\alpha\cos\alpha+\sin\alpha\sin2\alpha}=\\ =\frac{2\sin^22\alpha}{\sin2\alpha\sin\alpha+\sin\alpha\sin2\alpha}=\frac{2\sin^22\alpha}{2\sin2\alpha\sin\alpha}=\\ =\frac{\sin2\alpha}{\sin\alpha}=\frac{2\sin\alpha\cos\alpha}{\sin\alpha}=2\cos\alpha;\\ \frac{1-\cos4\alpha}{\cos\alpha-\cos3\alpha}=2\cos\alpha $$
что и требовалось доказать
Доказать тождество 1+sin2x=(sinx+cosx)^2
Решение: 1 + sin2x = (sinx + cosx)²
1 + sin2x = sin²x + 2 · sinx · cosx + cox²x
1 + sin2x = (sin²x + cos²x) + 2 · sinx · cosx
1 + sin2x = 1 + sin2x
Решение в скане.
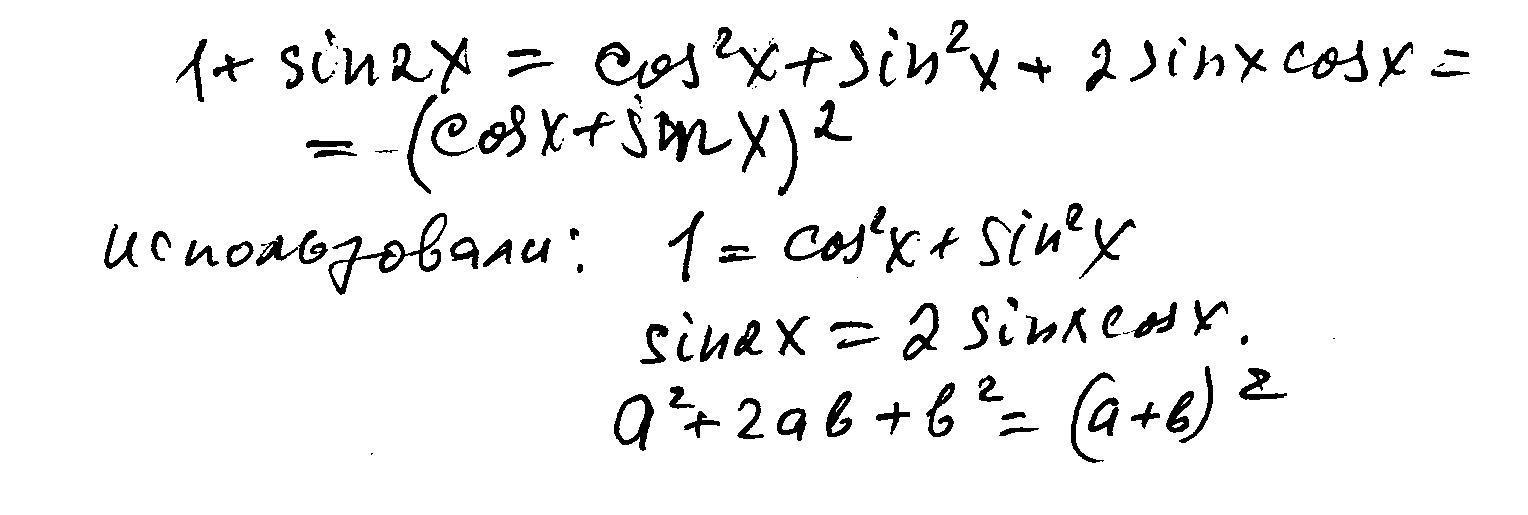
Помогите 8sin20 * cos40 * cos80 = 1 доказать тождество
Решение: Домножим все на cos20, получим:
8sin20 * cos20 * cos40 * cos80 = cos20. Т. к. 2*sin20*cos20=sin40, тогда:
4*sin40*cos40*cos80=cos20. Т. к. 2*sin40*cos40=sin80, то: 2*sin80*cos80=cos20. Получили, что: sin160=cos20. Вообще говоря, sin160=sin(180-20)=sin20. Очевидно, что равенство sin20=cos20 не верно, значит в исходном условии была опечатка. Если бы напечатали: 8*cos20*cos40*cos80=1, то домножив все на sin20, выполняя схожие действия мы бы пришли к равенству sin160=sin20, что верно ))